Stereometrie¶
Die Stereometrie ist das geometrische Teilgebiet, in dem Eigenschaften dreidimensionaler Grundformen untersucht werden. Hierbei sind für vielerlei Anwendungen insbesondere die Größe des Volumens und der Oberfläche von regelmäßigen Formen von Interesse.
Das Prinzip von Cavalieri
Schneidet man zwei geometrische Körper mit gleich große Grundfläche und gleicher Höhe in beliebig viele dünne „Scheiben“ (wobei die Schnitte stets durch beide Körper in gleicher Höhe verlaufen), so ist das Volumen beider Körper genau dann identisch, wenn jede dieser „Scheiben“ eine gleiche Grundfläche aufweist.
Wird beispielsweise, wie in der obigen Abbildung dargestellt, ein Stapel mit quadratischen Karteikarten seitlich verschoben, so bleibt dadurch das Volumen des Stapels unverändert. Die Karten könnten ebenso diagonal zerschnitten und in gedrehter Form aneinandergereiht werden; auch in diesem Fall würde sich das Volumen nicht ändern. Die einzelnen Grundflächen müssen für die Anwendung des Prinzips von Cavalieri somit nicht kongruent sein, sondern nur gleich große Flächeninhalte haben.
Quader, Würfel und Prisma¶
Quader und Würfel
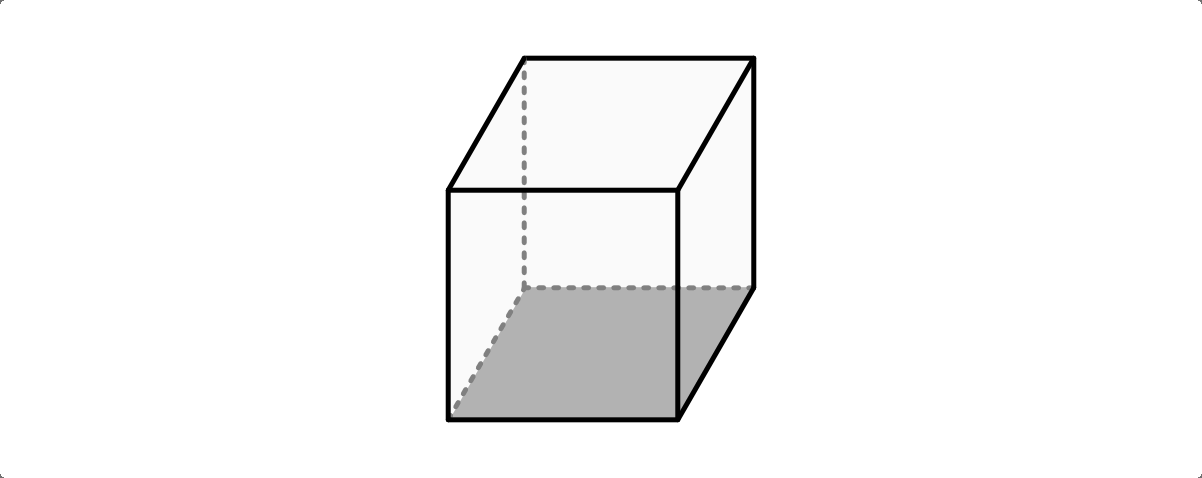
In einem Quader sind im Allgemeinen alle Seitenlängen unterschiedlich lang, alle
Winkel betragen 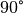 . Für das Volumen
. Für das Volumen 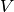 und die Oberfläche
und die Oberfläche
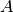 eines Quaders gilt:
eines Quaders gilt:
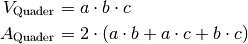
In einem Würfel – einer Sonderform eines Quaders – sind alle Seitenlängen
gleich lang, alle Winkel betragen 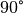 . Für das Volumen
. Für das Volumen 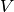 und
die Oberfläche
und
die Oberfläche 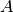 eines Würfels gilt:
eines Würfels gilt:
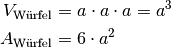
Prismen
Für das Volumen 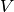 und die Oberfläche
und die Oberfläche 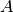 eines Prismas gilt:
eines Prismas gilt:
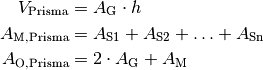
Pyramide und Pyramidenstumpf¶
Für das Volumen 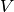 und die Oberfläche
und die Oberfläche 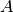 einer Pyramide gilt:
einer Pyramide gilt:
![V_{\mathrm{{Pyramide}}} &= \frac{A_{\mathrm{G}} \cdot h}{3} \\[4pt]
A_{\mathrm{{M, Pyramide}}} &= A_1 + A_2 + \ldots + A_{\mathrm{n}}\\
A_{\mathrm{{O, Pyramide}}} &= A_{\mathrm{G}} + A_{\mathrm{M}}](../_images/math/bbb5985ae33193c8049d44a71992f40039a5cb09.png)
Für das Volumen 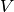 und die Oberfläche
und die Oberfläche 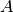 eines Pyramidenstumpfes
gilt:
eines Pyramidenstumpfes
gilt:
![V_{\mathrm{{Pyramidenstumpf}}} &= \frac{1}{3} \cdot h \cdot (A_{\mathrm{G}} +
\sqrt{A_{\mathrm{G}} \cdot A_{\mathrm{D}}} + A_{\mathrm{D}}) \\[4pt]
A_{\mathrm{{M, Pyramidenstumpf}}} &= A_1 + A_2 + \ldots + A
_{\mathrm{n}}\\
A_{\mathrm{{O, Pyramidenstumpf}}} &= A_{\mathrm{G}} + A_{\mathrm{M}} + A_{\mathrm{D}}](../_images/math/f3e681d7071558ee1cdda5c0bc7c096c9356862e.png)
Kugel und Kreiszylinder¶
Für das Volumen 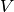 und die Oberfläche
und die Oberfläche 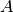 einer Kugel gilt:
einer Kugel gilt:
![V_{\mathrm{{Kugel}}} &= \frac{4}{3} \cdot \pi \cdot r^3 \\[4pt]
A_{\mathrm{{O, Kugel}}} &= 4 \cdot \pi \cdot r^2](../_images/math/dd17891ba45e28e513d6a7528ec8577a7eabcee9.png)
Für das Volumen 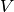 und die Oberfläche
und die Oberfläche 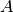 eines Kreiszylinders
gilt:
eines Kreiszylinders
gilt:
![V_{\mathrm{{Kreiszylinder}}} &= p \cdot r^2 \cdot h \\[4pt]
A_{\mathrm{{M, Kreiszylinder}}} &= 2 \cdot \pi \cdot r \cdot h \\
A_{\mathrm{{O, Kreiszylinder}}} &= 2 \cdot \pi \cdot r^2 + 2 \cdot \pi \cdot h](../_images/math/7785374d0effd002266bfa9e6450d77b2ee4d412.png)
Kreiskegel und Kreiskegelstumpf¶
Für das Volumen 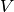 und die Oberfläche
und die Oberfläche 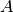 eines Kreiskegels gilt
mit
eines Kreiskegels gilt
mit 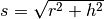 :
:
![V_{\mathrm{{Kreiskegel}}} &= \frac{\pi \cdot r^2 \cdot h}{3} \\[4pt]
A_{\mathrm{{M, Kreiskegel}}} &= \pi \cdot r \cdot s \\
A_{\mathrm{{O, Kreiskegel}}} &= \pi \cdot r^2 + \pi \cdot r \cdot s](../_images/math/54edf317459cf77ba8cb650f08b87514c5671a3c.png)
Für das Volumen 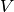 und die Oberfläche
und die Oberfläche 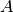 eines Kreiskegelstumpfes
gilt mit
eines Kreiskegelstumpfes
gilt mit 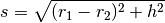 :
:
![V_{\mathrm{{Kreiskegelstumpf}}} &= \frac{\pi}{3} \cdot h \cdot \left( r_1^2
+ r_2^2 + r_1 \cdot r_2 \right) \\[4pt]
A_{\mathrm{{M, Kreiskegelstumpf}}} &= \pi \cdot s \cdot (r_1 + r_2) \\
A_{\mathrm{{O, Kreiskegelstumpf}}} &= \pi \cdot (r_1^2 + r_2^2 + s \cdot
(r_1 + r_2))](../_images/math/2526b0d4a5b9a1042b31204394feade2d639a70d.png)