Zusammenfassung wichtiger Ableitungsregeln¶
Im Folgenden sind die wichtigsten Ableitungsregeln der vorherigen Abschnitte nochmals kurz zusammengefasst.
Allgemeine Ableitungsregeln¶
Die folgenden Ableitungsregeln sind allgemein für beliebige Funktionen gültig:
Lässt sich eine Funktion
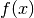 als Summe einer anderen Funktion
als Summe einer anderen Funktion
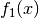 mit einem konstanten Summanden
mit einem konstanten Summanden  darstellen, so ist
ihre Ableitungsfunktion
darstellen, so ist
ihre Ableitungsfunktion 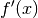 mit der Ableitung
mit der Ableitung 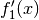 der
anderen Funktion identisch:
der
anderen Funktion identisch:(1)¶
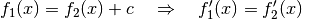
Insbesondere ist die Ableitung beziehungsweise Steigung einer konstanten Funktion
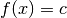 gleich Null.
gleich Null.Lässt sich eine Funktion
 als Produkt einer anderen Funktion
als Produkt einer anderen Funktion
 mit einem konstanten Faktor
mit einem konstanten Faktor  darstellen, so entspricht
ihre Ableitungsfunktion
darstellen, so entspricht
ihre Ableitungsfunktion 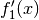 derjenigen der anderen Funktion
derjenigen der anderen Funktion
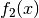 , wenn diese mit dem gleichen Faktor
, wenn diese mit dem gleichen Faktor  multipliziert
wird.
multipliziert
wird.(2)¶
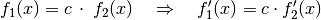
Für jede beliebige Funktion 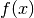 , die man sich aus zwei Teilfunktionen
, die man sich aus zwei Teilfunktionen
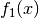 und
und 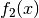 zusammengesetzt denken kann, sind folgende
Ableitungsregeln nützlich:
zusammengesetzt denken kann, sind folgende
Ableitungsregeln nützlich:
Additionsregel:
Besteht eine Funktion
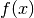 aus einer Summe zweier Teilfunktionen
aus einer Summe zweier Teilfunktionen
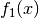 und
und 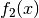 , so gilt für ihre Ableitung
, so gilt für ihre Ableitung 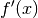 :
:(3)¶
![\left[ f_1(x) + f_2(x) \right]' = f_1'(x) + f_2'(x) {\color{white} \quad
\;\; \ldots}](../../_images/math/43bb1064bfe4aac0ae11be8c3d31fb030a526d02.png)
Produktregel:
Besteht eine Funktion
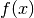 aus einem Produkt zweier Teilfunktionen
aus einem Produkt zweier Teilfunktionen
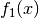 und
und 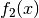 , so gilt für ihre Ableitung
, so gilt für ihre Ableitung 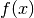 :
:(4)¶
![{\color{white} \ldots \quad \qquad} \left[ f_1(x) \, \cdot \; f_2(x)
\right]' = f_1'(x) \, \cdot \; f_2(x) \, + \, f_2'(x) \, \cdot \; f_1(x)](../../_images/math/51cf6d3396769a6a668d37bbba0cd811ed426b9d.png)
Quotientenregel:
Besteht eine Funktion
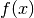 aus einem Quotienten zweier Teilfunktionen
aus einem Quotienten zweier Teilfunktionen
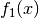 und
und 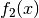 , so gilt für ihre Ableitung
, so gilt für ihre Ableitung 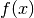 :
:(5)¶
![{\color{white} \ldots \qquad \qquad \quad \;\;\, } \left[
\frac{f_1(x)}{f_2(x)} \right]' = \frac{f_1'(x) \, \cdot \; f_2(x) \, - \,
f_2'(x) \, \cdot \; f_1(x)}{ \left( f_2(x) \right)^2}](../../_images/math/53ccebf4e1a521bde5f4644f3257013fd0e4e524.png)
Kettenregel
Besteht eine Funktion
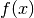 aus einer Verkettung zweier Teilfunktionen
aus einer Verkettung zweier Teilfunktionen 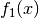 und
und
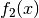 , so gilt für ihre Ableitung
, so gilt für ihre Ableitung 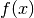 :
:(6)¶
![\left[ f_1\big(f_2(x)\big) \right]' = f_1'\big(f_2(x)\big) \, \cdot \;
f_2'(x)](../../_images/math/0c5fb07bce1625662de194f101de0850138e5d38.png)
Hierbei wird zunächst die Ableitung
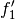 der äußeren Funktion
gebildet, wobei die innere Funktion unverändert gelassen wird. Der
resultierende Term wird anschließend mit der Ableitung der inneren Funktion
multipliziert.
der äußeren Funktion
gebildet, wobei die innere Funktion unverändert gelassen wird. Der
resultierende Term wird anschließend mit der Ableitung der inneren Funktion
multipliziert.
Satz von Rolle und Mittelwertsatz¶
Ist eine Funktion 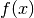 in einem Intervall
in einem Intervall ![]a;b[](../../_images/math/c5e78f5643ffe6b8e012ff569739024c278e9b30.png) stetig
differenzierbar und gilt zudem
stetig
differenzierbar und gilt zudem 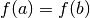 , so existiert mindestens eine
Stelle
, so existiert mindestens eine
Stelle 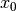 innerhalb des Intervalls, für die
innerhalb des Intervalls, für die 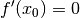 gilt.
Dieser Zusammenhang wird „Satz von Rolle“ genannt.
gilt.
Dieser Zusammenhang wird „Satz von Rolle“ genannt.
Anschaulich bedeutet der Satz von Rolle, dass es entlang eines stetig
verlaufenden Graphen zwischen zwei Kurvenpunkten mit übereinstimmenden
 -Werten mindestens einen Punkt gibt, an dem der Graph eine waagrechte
Tangente (Steigung Null) besitzt; insbesondere muss sich damit zwischen zwei
Nullstellen einer stetigen Funktion stets eine Extremstelle befinden.
-Werten mindestens einen Punkt gibt, an dem der Graph eine waagrechte
Tangente (Steigung Null) besitzt; insbesondere muss sich damit zwischen zwei
Nullstellen einer stetigen Funktion stets eine Extremstelle befinden.
Der Satz von Rolle kann auch allgemeiner formuliert werden: Ist eine Funktion
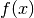 in einem Intervall
in einem Intervall ![]a ;\, b[](../../_images/math/a8adec5fa79c8dee561b6142037732c4a38ba156.png) stetig differenzierbar, so
existiert mindestens eine Stelle
stetig differenzierbar, so
existiert mindestens eine Stelle 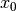 innerhalb des Intervalls, für die
gilt:
innerhalb des Intervalls, für die
gilt:
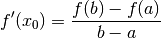
Dieser so genannte Mittelwertsatz besagt anschaulich, dass es entlang eines
stetig verlaufenden Graphen zwischen zwei Kurvenpunkten stets (mindestens) einen
Punkt 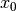 gibt, dessen Tangentensteigung gleich der Steigung der durch
gibt, dessen Tangentensteigung gleich der Steigung der durch
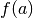 und
und 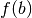 verlaufenden Sekante ist. Der Mittelwertsatz kann
somit als Erweiterung des Satzes von Rolle aufgefasst werden, da er diesen für
verlaufenden Sekante ist. Der Mittelwertsatz kann
somit als Erweiterung des Satzes von Rolle aufgefasst werden, da er diesen für
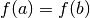 als Sonderfall enthält.
als Sonderfall enthält.
Ableitungsregeln wichtiger Funktionen¶
| Bezeichnung | 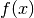 |
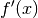 |
Bedingung(en) |
| Potenzfunktion | 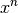 |
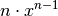 |
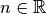 |
| Exponentialfunktion | 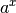 |
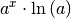 |
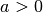 , , 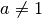 |
| Natürliche Exponentialfunktion | 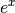 |
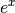 |
|
| Logarithmusfunktion | 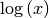 |
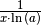 |
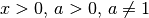 |
| Natürliche Logarithmusfunktion | 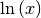 |
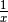 |
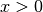 |
| Sinusfunktion | 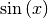 |
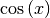 |
|
| Cosinusfunktion | 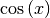 |
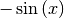 |
|
| Tangensfunktion | 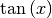 |
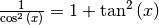 |
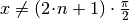 mit mit 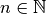 |
| Cotangensfunktion | 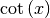 |
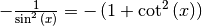 |
 mit mit 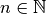 |
