Parabel – Scheitel und Öffnung¶
Bei dieser Übungsaufgabe geht es um das Differenzieren einer quadratischen Funktion.
Aufgabe:
Der Scheitel einer Parabel ist zu bestimmen. Es ist zu entscheiden, ob die Parabel nach unten oder nach oben geöffnet ist.
Lösung:
Die Orientierung einer Parabel kann man am Koeffizienten ihres quadratischen Terms ablesen; ist dieser positiv, so ist die Parabel nach oben, andernfalls nach unten geöffnet.
Der Scheitelpunkt ist das einzige Extremum einer Parabel. Um ihn zu bestimmen,
bildet man daher die erste Ableitung der quadratischen Funktion und setzt diese
gleich Null. So erhält man den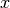 
-Wert des Scheitelpunktes. Den
zugehörigen 
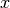-Wert erhält man, indem man den -Wert des
Scheitelpunktes in die ursprüngliche Funktionsgleichung einsetzt.
Mit Sympy kann die Aufgabe folgendermaßen gelöst werden:
import sympy as sy
# Funktionsgleichung als String einlesen:
parable_function_input = input("Bitte die Funktionsgleichung einer Parabel \
eingeben (beispielsweise 3*x**2 - 5*x +7): ")
# Eingelesenen String in Sympy-Ausdruck umwandeln:
parable_function = sy.S(parable_function_input)
# Orientierung der Parabel bestimmen:
if parable_function.coeff(x, n=2) > 0:
orientation = "up"
else:
orientation = "down"
# Erste und zweite Ableitung bilden:
parable_function_diff_1 = sy.diff(parable_function, x, 1)
parable_function_diff_2 = sy.diff(parable_function, x, 2)
# Extremstelle bestimmen (liefert Liste an Ergebnissen):
extremes = sy.solve(sy.Eq(parable_function_diff_1, 0))
# Der gesuchte x_0-Wert ist der einzige Eintrag der Ergebnisliste:
x_0 = extremes[0]
# Zugehörigen Funktionswert bestimmen:
y_0 = parable_function.subs(x, x_0)
print("Die Orientierung der Parabel ist \"%s\", ihr Scheitel liegt bei \
(%.2f, %.2f)." % (orientation, x_0, y_0) )