Mathematischer Formelsatz¶

LaTeX unterstützt wie kaum ein anderes Textsatzungsprogramm das Einfügen mathematischer Formeln. Wahlweise können Formeln innerhalb einer Absatzes („Inline“) oder als eigenständiger Absatz in ein Dokument eingefügt werden: [1]

Mit $ Formel $ wird eine Formel innerhalb eines Textabsatzes eingefügt.
Mit $$ Formel $$ wird eine Formel als eigenständiger Absatz zentriert eingefügt.

Sollen auch Zeilenumbrüche innerhalb einer Formel erlaubt sein, so sollte die Umgebung align (beziehungsweise align* für nummerierte beziehungsweise nicht nummerierte Formeln) gewählt werden:

% Standard-Mathe-Umgebung:
\begin{align}
    E \underset{Einstein}{=} m \cdot c^2
    \underset{Pythagoras}{=} m \cdot (a^2 + b^2)
\end{align}

Ergebnis:

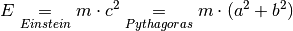
(1)¶ $E \underset{Einstein}{=} m \cdot c^2 \underset{Pythagoras}{=} m \cdot (a^2 + b^2)$

Der Gleichungs-Zähler kann bei Bedarf mittels \setcounter{equation}{1} wieder auf den Wert 1 (oder einen beliebigen anderen Wert) gesetzt werden. Mit \numberwithin{equation}{section} kann zudem festgelegt werden, welcher Gliederungstiefe die Formeln zugerechnet werden sollen, ob also eine Nummerierung in der Art 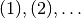$(1), (2), \ldots$ oder abschnittsweise als 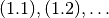$(1.1), (1.2), \ldots$ erfolgen soll.

Formeln mit mehreren Nummerierungen

Die Umgebungen align und align* sind für fast alle abgesetzten Formeln die beste Wahl. Eine Ausnahme bilden mehrere einzeilige Formeln, die zueinander ausgerichtet, aber einzeln nummeriert werden sollen. Für diesen Zweck gibt es die Umgebung eqnarray:

% Umgebung für mehrere nummerierte Zeilen:
\begin{eqnarray}
    x^2 &=& 2 \\
    \to x &=& \pm \sqrt{2}
\end{eqnarray}

Ergebnis:

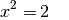
(2)¶ $x^2 =& \, 2 {\color{white};;;}\\$

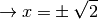
(3)¶ $\to x =& \pm \sqrt{2}$

Sollen bei verwendung einer eqnarray-Umgebung einzelne Zeilen nicht nummeriert werden, so kann man am Ende der jeweiligen Zeile die Anweisung \notag einfügen, um eine Nummerierung zu verhindern.

Sollen die einzelnen Zeilen eines Formel-Absatzes zwar eigenständig nummeriert werden und eigene Labels erhalten, aber letztlich nur als Teile einer ganzen Formel angesehen werden, so ist dies mittels der subequations-Umgebung möglich:

Beispiel:

\begin{subequations}
\label{maxwell-gleichungen}
    \begin{align}
        \text{div }(\vec{D}) &= 4 \cdot \pi \cdot \rho
        \label{coulomb-gesetz}\\
        \text{rot }(\vec{H}) &= \frac{4 \cdot \pi}{c} \cdot \vec{j}
        \label{ampere-gesetz}\\
        \text{rot }(\vec{E}) &= - \frac{1}{c} \cdot \frac{\partial \vec{B}}{\partial t}
        \label{faraday-gesetz-1} \\
        \text{div }(\vec{B}) &= 0
        \label{faraday-gesetz-2}
    \end{align}
\end{subequations}

Ergebnis:

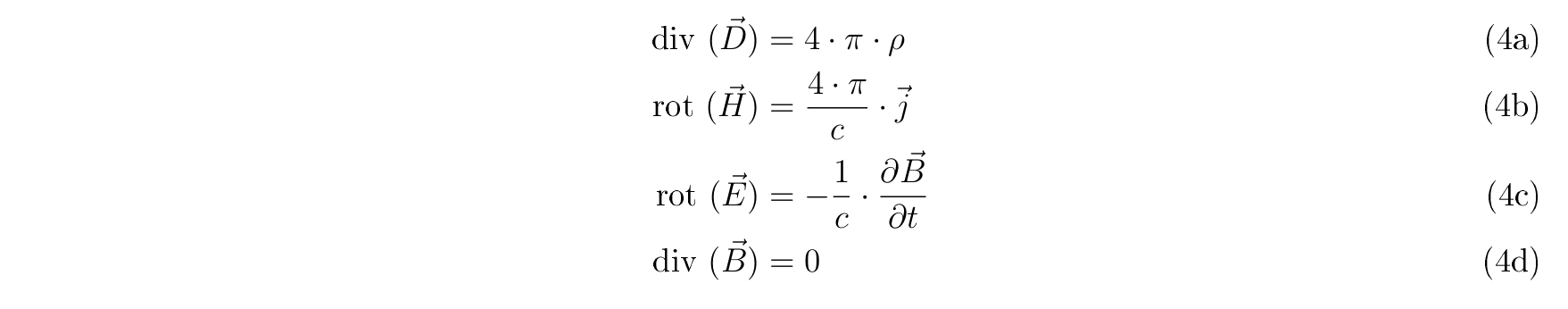
Auf einzelne Gleichungen kann dann via \eqref{} wahlweise auf ein Label der Teilgleichung oder auch auf das Label der gesamten Gleichung verwiesen werden.

Besonderheiten im Mathematik-Modus

Der Mathematik-Modus weist gegenüber normalem Text einige Besonderheiten auf:

Mathematische Formeln dürfen keine leeren Zeilen beinhalten: Jede Formel entspricht einem einzigen Absatz.
Leerzeichen innerhalb von Formeln werden ignoriert und müssen bei Bedarf manuell mittels Abstands-Anweisungen wie \, oder \; gesetzt werden. Vor und nach mathematischen Operatoren wie + oder - wird von LaTeX automatisch etwas Freiraum eingefügt.
Buchstaben werden in Formeln grundsätzlich als Namen von Variablen interpretiert und daher kursiv gedruckt. Sollen einzelne Buchstaben aufrecht gedruckt werden, so ist dies mittels \mathrm{} möglich; normale Textabschnitte (inklusive Leerzeichen) können innerhalb von Formeln mittels \text{Text} eingebettet werden.

Mathematische Symbole¶

Griechisches Alphabet

In Formeln werden sehr häufig griechische Buchstaben als Variablenbezeichnungen verwendet. In der folgenden Liste sind die griechischen Buchstaben sowie die zugehörigen LaTeX-Anweisungen für den Mathe-Modus aufgelistet.

Griechisches Alphabet¶
Aussprache	Buchstabe	LaTeX-Code	Aussprache	Buchstabe	LaTeX-Code
Alpha	$A \quad \alpha$	`A \alpha`	Ny	$N \quad \nu$	`N \nu`
Beta	$B \quad \beta$	`B \beta`	Xi	$\Xi \quad \xi$	`\Xi \xi`
Gamma	$\Gamma \quad \gamma$	`\Gamma \gamma`	Omikron	$O \quad o$	`O o`
Delta	$\Delta \quad \delta$	`\Delta \delta`	Pi	$\Pi \quad \pi$	`\Pi \pi`
Epsilon	$E \quad \varepsilon$	`E \varepsilon`	Rho	$P \quad \rho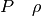$	`P \rho`
Zeta	$Z \quad \zeta$	`Z \zeta`	Sigma	$\Sigma \quad \sigma$	`\Sigma \sigma`
Eta	$H \quad \eta$	`H \eta`	Tau	$T \quad \tau$	`T \tau`
Theta	$\varTheta \quad \vartheta$	`\varTheta \vartheta`	Ypsilon	$\Upsilon \quad \upsilon$	`\Upsilon \upsilon`
Iota	$I \quad \iota$	`I \iota`	Phi	$\varPhi \quad \varphi$	`\varPhi \varphi`
Kappa	$K \quad \kappa$	`K \kappa`	Chi	$X \quad \chi$	`X \chi`
Lambda	$\Lambda \quad \lambda$	`\Lambda \lambda`	Psi	$\Psi \quad \psi$	`\Psi \psi`
My	$M \quad \mu$	`M \mu`	Omega	$\Omega \quad \omega$	`\Omega \omega`

Bei manchen griechischen Buchstaben existiert neben den oben angegebenen Varianten auch noch alternative Darstellungen. Beispielsweise wird \theta als 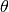$\theta$ ausgegeben, während \vartheta als 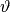$\vartheta$ gedruckt wird.

Mathematische Schriftarten

Ebenso wie Texte in normalen Textabsätzen mittels \textbf{}, \textit{} usw. hervorgehoben werden können, existieren im Mathe-Modus verschiedene Möglichkeiten, die Form oder den Typ einer Schrift zu verändern:

Ohne explizite Angabe wird \mathnormal{} als Schrifttyp verwendet. Hierbei werden Buchstaben kursiv dargestellt, Zahlen hingegen aufrecht: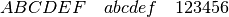

$ABCDEF \quad abcdef \quad 123456$

Mit \mathrm{} („Math Roman“) werden sowohl Buchstaben als auch Zahlen im Mathe-Modus aufrecht gedruckt. Dieser Schrifttyp wird beispielsweise geometrische Punkte, für Einheiten oder Symbole in Indizes verwendet.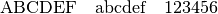

$\mathrm{ABCDEF} \quad \mathrm{abcdef} \quad \mathrm{123456}$

Mit \mathit{} („Math Italic“) werden sowohl Buchstaben als auch Zahlen im Mathe-Modus kursiv gedruckt: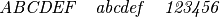

$\mathit{ABCDEF} \quad \mathit{abcdef} \quad \mathit{123456}$

Mit \mathbf{} („Math Bold Font“) werden Buchstaben und Zahlen im Mathe-Modus aufrecht und fettgedruckt ausgegeben. In manchen Lehrbüchern werden auf diese Weise Vektoren gekennzeichnet.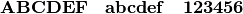

$\mathbf{ABCDEF} \quad \mathbf{abcdef} \quad \mathbf{123456}$

Mit \mathsf{} („Math Sans Serif“) werden Buchstaben und Zahlen im Mathe-Modus aufrecht und ohne Serifen ausgegeben: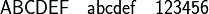

$\mathsf{ABCDEF} \quad \mathsf{abcdef} \quad \mathsf{123456}$

Mit \mathtt{} („Math Typesetter“) werden Buchstaben und Zahlen im Mathe-Modus aufrecht und nicht-proportional ausgegeben: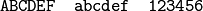

$\mathtt{ABCDEF} \quad \mathtt{abcdef} \quad \mathtt{123456}$

Mit \mathfrak{} („Math Fraktur“) werden Buchstaben und Zahlen im Mathe-Modus als Frakturschrift ausgegeben: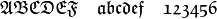

$\mathfrak{ABCDEF} \quad \mathfrak{abcdef} \quad \mathfrak{123456}$

Mit \mathbb{} („Math Blackboard Bold“) werden Großbuchstaben im Mathe-Modus als Mengensymbole ausgegeben. Hierzu muss in der Präambel das Paket amsfonts mittels \usepackage{amsfonts} geladen werden.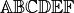

$\mathbb{ABCDEF}$

Mit \mathcal} („Math Calligraphy“) werden Großbuchstaben im Mathe-Modus kalligraphisch ausgegeben: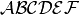

$\mathcal{ABCDEF}$

Mit \mathscr{} („Math Script“) werden Großbuchstaben im Mathe-Modus in einer weiteren Darstellungsvariante ausgegeben. Hierzu muss in der Präambel das Paket mathrsfs mittels \usepackage{mathrsfs} geladen werden.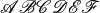

$\mathscr{ABCDEF}$

Relationszeichen

Die Relationszeichen 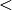$=$ , $<$ und 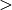$>$ können direkt mittels der Tastatur eingegeben werden. Weitere Relationszeichen sind in der folgenden Tabelle aufgelistet.

Eingabe	Ausgabe	Eingabe	Ausgabe
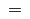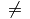`=`	${\color{white}\|}={\color{white}\|}$	`\neq`	${\color{white}\|}\neq{\color{white}\|}$
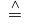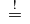`\stackrel{\wedge}=`	${\color{white}\|}\stackrel{\wedge}={\color{white}\|}$	`\stackrel{!}=`	${\color{white}\|}\stackrel{!}={\color{white}\|}$
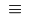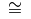`\equiv`	${\color{white}\|}\equiv{\color{white}\|}$	`\cong`	${\color{white}\|}\cong{\color{white}\|}$
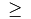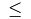`\geq`	${\color{white}\|}\geq{\color{white}\|}$	`\leq`	${\color{white}\|}\leq{\color{white}\|}$
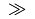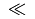`\gg`	${\color{white}\|}\gg{\color{white}\|}$	`\ll`	${\color{white}\|}\ll{\color{white}\|}$
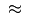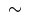`\approx`	${\color{white}\|}\approx{\color{white}\|}$	`\sim`	${\color{white}\|}\sim{\color{white}\|}$
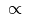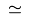`\propto`	${\color{white}\|}\propto{\color{white}\|}$	`\simeq`	${\color{white}\|}\simeq{\color{white}\|}$
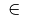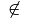`\in`	${\color{white}\|}\in{\color{white}\|}$	`\not\in`	${\color{white}\|}\not\in{\color{white}\|}$
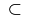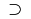`\subset`	${\color{white}\|}\subset{\color{white}\|}$	`\supset`	${\color{white}\|}\supset{\color{white}\|}$
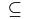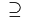`\subseteq`	${\color{white}\|}\subseteq{\color{white}\|}$	`\supseteq`	${\color{white}\|}\supseteq{\color{white}\|}$
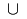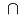`\cup`	${\color{white}\|}\cup{\color{white}\|}$	`\cap`	${\color{white}\|}\cap{\color{white}\|}$
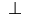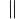`\perp`	${\color{white}\|}\perp{\color{white}\|}$	`\parallel`	${\color{white}\|}\parallel{\color{white}\|}$

Allgemein können die obigen Relationssymbole, wie am Beispiel 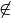$\not\in$ (\not \in) gezeigt, durch ein Voranstellen von \not invertiert werden; beispielsweise ergibt eine Eingabe von \not\ge das Zeichen 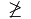${\color{white}|}\not\ge{\color{white}|}$ .

Weitere mathematische Symbole

Eingabe	Ausgabe	Eingabe	Ausgabe
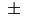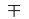`\pm`	${\color{white}\|}\pm{\color{white}\|}$	`\mp`	${\color{white}\|}\mp{\color{white}\|}$
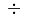`\div{}`	${\color{white}\|}\div{}{\color{white}\|}$	`\setminus`	${\color{white}\|}\setminus{\color{white}\|}$
`\cdot`	${\color{white}\|\|\!}\cdot{\color{white}\|}$	`\times`	${\color{white}\|}\times{\color{white}\|}$
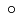`\ast`	${\color{white}\|}\ast{\color{white}\|}$	`\star`	${\color{white}\|}\star{\color{white}\|}$
`\circ`	${\color{white}\|}\circ{\color{white}\|}$	`\bullet`	${\color{white}\|}\bullet{\color{white}\|}$
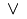`\varangle`	${\color{white}\|\|\!}\varangle{\color{white}\|}$	`\angle`	${\color{white}\|}\angle{\color{white}\|}$
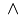`\vee`	${\color{white}\|}\vee{\color{white}\|}$	`\wedge`	${\color{white}\|}\wedge{\color{white}\|}$
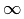`\forall`	${\color{white}\|\|}\forall{\color{white}\|}$	`\exists`	${\color{white}\|\|}\exists{\color{white}\|}$
`\infty`	${\color{white}\|}\infty{\color{white}\|}$	`\emptyset`	${\color{white}\|\|}\emptyset{\color{white}\|}$
`\partial`	${\color{white}\|\|}\partial{\color{white}\|}$	`\nabla`	${\color{white}\|}\nabla{\color{white}\|}$
`\oplus`	${\color{white}\|}\oplus{\color{white}\|}$	`\ominus`	${\color{white}\|}\ominus{\color{white}\|}$
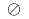`\odot`	${\color{white}\|}\odot{\color{white}\|}$	`\oslash`	${\color{white}\|}\oslash{\color{white}\|}$
`\Box`	${\color{white}\|\|}\Box{\color{white}\|}$	`\checkmark`	${\color{white}\|\|}\checkmark{\color{white}\|}$
`\clubsuit`	${\color{white}\|\|}\clubsuit{\color{white}\|}$	`\spadesuit`	${\color{white}\|\|}\spadesuit{\color{white}\|}$
`\heartsuit`	${\color{white}\|\|}\heartsuit{\color{white}\|}$	`\diamondsuit`	${\color{white}\|\|}\diamondsuit{\color{white}\|}$
`\%`	${\color{white}\|\|}\%{\color{white}\|}$	`\permil`	${\color{white}\|\|}\permil{\color{white}\|}$

Die Anweisung \permil setzt voraus, dass in der Präambel das Paket wasysym geladen wird (\usepackage{wasysym}).

Mathematische Ausdrücke¶

Indizes und Exponenten

Soll im Mathe-Modus eine einzelne Ziffer oder ein einzelner Buchstabe als Index einer Variablen gesetzt werden, so ist dies mittels x_1, x_2, ..., x_n möglich; die Ausgabe würde in diesem Fall 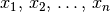$x_1,\, x_2,\, \ldots,\, x_n$ lauten. Soll der Index aus mehr als einem Zeichen bestehen, so müssen diese in geschweifte Klammern gesetzt werden, also beispielsweise x_{1,2} für 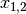$x _{1,2}$ . Lässt man die geschweiften Klammern weg, so springt LaTeX nach dem ersten Index-Zeichen wieder in den normalen Mathe-Modus zurück und druckt die restlichen Zeichen als normal große Variablennamen.

Um im Mathe-Modus eine einzelne Ziffer oder einen einzelnen Buchstaben als Exponent einer Variablen zu setzen, so ist dies mittels x^1, x^2, ..., x^n möglich; die Ausgabe würde in diesem Fall 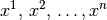$x^1,\, x^2,\, \ldots, x^n$ lauten. Auch bei Exponenten müssen geschweifte Klammern gesetzt werden, sofern diese aus mehr als einem Zeichen bestehen.

In Exponenten werden Buchstaben in LaTeX standardmäßig aufrecht gedruckt, in Indizes hingegen kursiv. Möchte man, wie es in der Textsatzung üblich ist, aufrechte Indizes erhalten, so müssen diese in geschweifte Klammern gesetzt und mittels \mathrm{} explizit in aufrechter Form ausgegeben werden (Zahlen werden auch in LaTeX stets aufrecht gedruckt).

Einheiten

In Mathe-Umgebungen können Einheiten – ebenso wie in normalen Text-Bereichen – am einfachsten mittels des units-Pakets gesetzt werden. Die Syntax dafür ist denkbar einfach:

Beispiel:

% Größe mit Einheit setzen:
\unit[1]{Liter} = \unit[1]{dm^3}

Ergebnis:

$% Größe mit Einheit setzen: \unit[1]{Liter} = \unit[1]{dm^3}$

Die units-Anweisung hat einerseits den Effekt, dass die in den geschweiften Klammern angegebene Einheit nicht wie im Mathe-Modus üblich kursiv, sondern aufrecht gedruckt wird; andererseits wird der Abstand zwischen dem Zahlenwert und der Einheit etwas reduziert. Die units{}-Anweisung kann auch ohne Angabe eines Zahlenwerts genutzt werden, beispielsweise um reine Einheits-Gleichungen zu setzen. Innerhalb der geschweiften Klammern sind auch weitere LaTeX-Anweisungen, wie beispielsweise Brüche oder Wurzeln, erlaubt.

Klammern

Runde und eckige Klammern können in LaTeX-Formeln als gewöhnliche Zeichen gesetzt werden, bei geschweiften Klammern muss ein Backslash-Zeichen vor die öffnende und schließende Klammer gesetzt werden.

Beispiel:

% Verschiedene Klammern in LaTeX:
(a)     \qquad [b] \qquad \{c\} \qquad |d| \quad \langle e \rangle

Ergebnis:

$(a) \qquad [b] \qquad \{c\} \qquad |d| \quad \langle e \rangle$

Möchte man die Größe einer Klammer anpassen, wenn beispielsweise ein Bruch innerhalb der Klammer vorkommt, so kann die Klammergröße automatisch oder manuell festgelegt werden:

Mit \left und \right wird die Größe der darauf folgenden öffnenden beziehungsweise schließenden Klammer automatisch an den Inhalt der Klammer angepasst. Für runde Klammern mit autoamtische Größenanpassung kann man also \left( beziehungsweise \right) schreiben:

Beispiel:
```
(a^{b^{c^d}}) \ne \left( d^{c^{b^a}} \right)
```
Ergebnis:

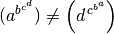
$(a^{b^{c^d}}) \ne \left( d\;\!^{c^{b^a}} \right)$

Das gleiche funktioniert auch mit eckigen und geschweiften Klammern, wobei bei letzteren \left\{ beziehungsweise \right\} geschrieben werden müssen.
Mit \big( ... \big), \Big( ... \Big), \bigg( ... \bigg) oder \Bigg( ... \Bigg) kann die Größe der öffnenden beziehungsweise schließenden runden Klammern manuell festgelegt werden. Das gleiche funktioniert ebenfalls mit vertikalen Strichen (beispielsweise Betragstrichen), die direkt mittels des Pipe-Zeichens | eingegeben werden können.

Bisweilen sind auch „liegende“ geschweifte Klammern nützlich, um beispielsweise eine Erklärung für einen auftretenden Term in die Gleichung mit aufzunehmen. Bindet man in der Präambel das Paket mathtools mit ein, so kann man dafür Anweisung die Anweisungen \underbrace{} beziehungsweise \overbrace{} nutzen:

Beispiel:

 \overbrace{n \cdot n \cdot n \cdot \ldots \cdot n}^{\text{$k$ mal} } = n^k \\
\underbrace{n \cdot n \cdot n \cdot \ldots \cdot n}_{\text{$k$ mal} } = n^k

Ergebnis:

$\overbrace{n \cdot n \cdot n \cdot \ldots \cdot n}^{\text{$k$ mal} } &= n^k \\[6pt] \underbrace{n \cdot n \cdot n \cdot \ldots \cdot n}_{\text{$k$ mal} } &= n^k$

Pfeile

Pfeile können entweder über oder zwischen mathematischen Symbolen stehen. Pfeile über mathematischen Symbolen markieren Vektoren oder gerichtete Strecken. Im Fall von Vektoren, wenn sich der Pfeil über ein einzelnes Zeichen erstreckt, kann man die Anweisung \vec{} verwenden, für Pfeile über mehreren mathematischen Symbolen muss hingegen \overrightarrow{} (oder \overline{} für Strecken ohne Richtung) verwendet werden:

Beispiel:

\begin{align*}
    \vec{a}
    \overrightarrow{\mathrm{BC}}
    \overline{\mathrm{DE}}
\end{align*}

Ergebnis:

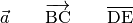
$\vec{a} \qquad \overrightarrow{\mathrm{BC}} \qquad \overline{\mathrm{DE}}$

Für Pfeile zwischen mathematischen Symbolen gibt es mehrere Anweisungen. Ein einfacher waagrechter Pfeil, wie er beispielsweise geschrieben wird, wenn eine Zahl gegen einen bestimmten Grenzwert geht, kann einfach mit \to gesetzt werden. Mehr Flexibilität bieten die Anweisungen der Art \leftarrow und \rightarrow:

LaTeX-Code	Ergebnis	Beschreibung
`\leftarrow` und `\rightarrow`	$\leftarrow \;\; \text{ und } \;\; \rightarrow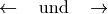$	waagrechter Pfeil
`\Leftarrow` und `\Rightarrow`	$\Leftarrow \;\; \text{ und } \;\; \Rightarrow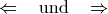$	waagrechter Pfeil mit Doppelstrich
`\longleftarrow` und `\longrightarrow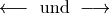`	$\longleftarrow \text{ und } \longrightarrow$	langer waagrechter Pfeil
`\Longleftarrow` und `\Longrightarrow`	$\Longleftarrow \text{ und } \Longrightarrow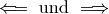$	langer waagrechter Pfeil mit Doppelstrich
`\leftrightarrow` und `\Leftrightarrow`	$\leftrightarrow \;\; \text{ und } \;\; \Leftrightarrow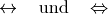$	beidseitiger Pfeil
`\longleftrightarrow` und `\Longleftrightarrow`	$\Longleftrightarrow \! \text{ und } \! \Longleftrightarrow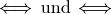$	langer beidseitiger Pfeil

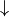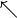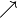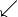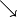Mittels \uparrow und \downarrow lassen sich entsprechend nach oben ( $\uparrow$ ) beziehungsweise nach unten ( $\downarrow$ ) zeigende Pfeile setzen; auch diese können wie \leftarrow und \rightarrow gemäß der obigen Tabelle modifiziert werden. Für diagonale Pfeile gibt es die Anweisungen \nwarrow und \nearrow ( $\nwarrow$ und $\nearrow$ ) beziehungsweise \swarrow und \searrow ( $\swarrow$ und $\searrow$ ), wobei die ersten beiden Buchstaben jeweils die Himmelsrichtung angeben, in die der Pfeil zeigen soll.

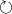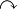Mittels \circlearrowleft und \circlearrowright lassen sich die zur Kennzeichnung von Drehmomenten verwendeten kreisförmige Pfeile ( $\circlearrowleft$ und $\circlearrowright$ ) setzen, mittels \curvearrowleft beziehungsweise \curvearrowright gebogene Pfeile ( $\curvearrowleft$ und $\curvearrowright$ ).

Beschriftete waagrechte Pfeile können zudem mittels \xleftarrow{} beziehungsweise \xrightarrow{} erstellt werden. Die Länge eines solchen Pfeils wird von LaTeX automatisch anhand der Länge des über beziehungsweise unter dem Pfeil stehenden Textes bestimmt.

Beispiel:

\mathrm{A} \quad \xleftarrow[\phantom{\text{was sonst?}}]{-1} \quad
\mathrm{B} \quad \xrightarrow[\text{was sonst?}]{+1} \quad C

Ergebnis:

$\mathrm{A} \quad \xleftarrow[\phantom{\text{was sonst?}}]{-1} \quad \mathrm{B} \quad \xrightarrow[\text{was sonst?}]{+1} \quad C$

Eine vollständige Übersicht über die verschiedenen Pfeil gibt es beispielsweise hier.

Wurzeln, Brüche und Binomialkoeffizienten

Wurzeln werden in LaTeX-Formeln mittels \sqrt{} gesetzt. Möchte man keine Quadrat-Wurzel ausgeben, sondern eine Wurzel mit einem anderen Wurzelexponenten, so kann für die 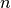$n$ -te Wurzel aus einer Zahl \sqrt[n]{Zahl} geschrieben werden.

Beispiel:

% "Normale" Quadrat-Wurzel:
\sqrt{16} = 4

% Kubische Wurzel:
\sqrt[3]{8} = 2

Ergebnis:

$\sqrt{16} = 4 \\[8pt] \sqrt[3]{8} = 2$

Innerhalb der \sqrt{}-Anweisung können auch andere Mathe-Anweisungen wie Pfeile oder Brüche gesetzt werden; Diese werden in LaTeX mittels \frac{Zähler}{Nenner} gesetzt:

Beispiel:

\begin{align*}
    \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c}
\end{align*}

Ergebnis:

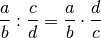
$\frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c}$

Innerhalb des Zähler und/oder Nenners können wiederum \frac{}-Anweisungen auftreten, so dass sich damit auch verschachtelte Brüche bilden lassen. Die Größe der Schriften sowie die Dicke der Bruchstriche werden dabei automatisch angepasst:

Beispiel:

\begin{align*}
    \frac{\frac{a}{b}}{\frac{c}{d}} = \frac{a \cdot d}{b \cdot c}
\end{align*}

Ergebnis:

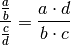
$\frac{\frac{a}{b}}{\frac{c}{d}} = \frac{a \cdot d}{b \cdot c}$

Die automatische Anpassung der Schriftgröße bei der \frac{}-Anweisung kann umgangen werden, wenn man mit ansonsten gleicher Syntax die \tfrac{} oder \dfrac{}-Anweisung verwendet:

Bei der \tfrac{}-Anweisung wird automatisch die Option \textstyle aktiviert; der Bruch wird dadurch möglichst so dimensioniert, dass er in eine normale Textzeile passt.
Bei der \dfrac{}-Anweisung wird automatisch die Option \displaystyle aktiviert; eine automatische Verkleinerung der Schriftgröße findet dabei auch bei verschachtelten Brüchen nicht statt.

In ähnlicher Weise wie Brüche lassen sich auch Binomial-Koeffizienten setzen. Auch wenn diese aus mathematischer Sicht eine andere Bedeutung haben, sind sie aus Sicht der Textsatzung den Brüchen ähnlich, nur dass der Bruchstrich zwischen der oberen und der unteren Zahl fehlt.

Beispiel:

% Binomialkoeffizient:
\begin{align*}
    \binom{n}{k} = \frac{n!}{(n - k)! \cdot k!}
\end{align*}

Ergebnis:

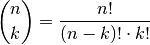
$\binom{n}{k} = \frac{n!}{(n - k)! \cdot k!}$

Summen, Produkte und Integrale

Das Summenzeichen 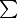$\sum$ kann im Mathe-Modus mittels \sum gedruckt werden. Üblicherweise wird dabei unterhalb des Summenzeichens die Untergrenze und oberhalb die Obergrenze der zu summierenden Größe angegeben. In LaTeX wird dazu die für Indizes und Exponenten übliche Syntax genutzt und somit \sum_{}^{} geschrieben:

Beispiel:

\begin{align*}
    \sum_{i=1}^{n} i =  \frac{n \cdot (n+1)}{2}
\end{align*}

Ergebnis:

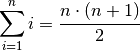
$\sum_{i=1}^{n} i = \frac{n \cdot (n+1)}{2}$

In gleicher Weise kann das (seltener vorkommende) Produkt-Zeichen 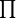$\prod$ genutzt werden:

Beispiel:

\begin{align*}
    \sum_{i=1}^{n} i =  \frac{n \cdot (n+1)}{2}
\end{align*}

Ergebnis:

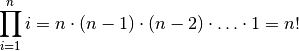
$\prod_{i=1}^{n} i = n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot 1 = n!$

Das Integralzeichen 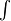$\int$ kann im Mathe-Modus mittels \int gedruckt werden. Üblicherweise wird auch hierbei unterhalb des Integralzeichens die Untergrenze und oberhalb die Obergrenze der zu integrierenden Größe angegeben. In LaTeX wird dazu wiederum die für Indizes und Exponenten übliche Syntax genutzt und somit \int_{}^{} geschrieben. Ohne weitere Voreinstellungen werden die Integralgrenzen etwas versetzt gedruckt; möchte man dies unterbinden, so kann man dies durch ein Einfügen von \limits vor den Integralgrenzen erreichen:

Beispiel:

\begin{align*}
    \int_{a}^{b}        f(x) \cdot \mathrm{d} x = F(b) - F(a) \\
    \int\limits_{a}^{b} f(x) \cdot \mathrm{d} x = F(b) - F(a)
\end{align*}

Ergebnis:

$\int_{a}^{b} f(x) \cdot \mathrm{d} x &= F(b) - F(a) \\[4pt] \int\limits_{a}^{b} f(x) \cdot \mathrm{d} x &= F(b) - F(a)$

Mehrfachintegrale (Flächen- und Volumenintegrale) können entsprechend mittels \iint, \iiint gesetzt werden, geschlossene Linien-Integrale mittels \oint.

Beispiel:

% Gaußscher Integralsatz:
\iiint_{V}^{} \text{div } \vec{E} (\vec{r}) \cdot \mathrm{d}^3 r  =
\oint\limits_{S(V)}^{} \vec{E} \cdot \mathrm{d} \vec{f}

Ergebnis:

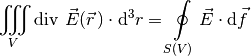
$\iiint_{V}^{} \text{div } \vec{E} (\vec{r}\,) \cdot \mathrm{d}^3 r = \oint\limits_{S(V)}^{} \vec{E} \cdot \mathrm{d} \vec{f}$

Matrizen und Determinanten

Zum Setzen von Matrizen beziehungsweise Determinanten stellt das Paket amsmath für den Mathe-Modus mehrere Umgebungen bereit:

`matrix`	Matrizen ohne Klammern
`pmatrix`	Matrizen mit runden Klammern
`bmatrix`	Matrizen mit eckigen Klammern
`vmatrix`	Matrizen mit eckigen Betragstrichen

Innerhalb einer Matrix-Umgebung werden die einzelnen Spalten, ähnlich wie bei Tabellen, durch &-Zeichen getrennt; Zeilenumbrüche lassen sich wie gewöhnlich mittels \\ erreichen.

Beispiel:

\begin{pmatrix}
    a_{11} & a_{12} & \cdots & a_{1n} \\
    a_{21} & a_{22} & \cdots & a_{2n} \\
    \vdots & \vdots & \ddots & \vdots \\
    a_{n1} & a_{n2} & \cdots & a_{nn}
\end{pmatrix}

Ergebnis:

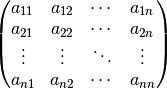
$\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix}$

Die vmatrix-Umgebung kann insbesondere zur Erzeugung von Determinanten genutzt werden; mittels der pmatrix-Umgebung hingegen können auch Vektoren als einspaltige Matrizen gesetzt werden.

Fallunterscheidungen

Fallunterscheidungen können im Mathe-Modus mittels der cases-Umgebung verwirklicht werden. Innerhalb einer solchen Umgebung können die einzelnen Elemente mittels eines &-Zeichens ausgerichtet werden; die vertikale Ausrichtung übernimmt LaTeX (bis auf manuell zu setzende Zeilenumbrüche) automatisch.

Beispiel:

| a | = \begin{cases}
    +a     & \text{ falls } a > 0 \\
    \;\;0  & \text{ falls } a = 0 \\
    -a     & \text{ falls } a < 0
\end{cases}

Ergebnis:

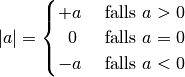
$| a | = \begin{cases} +a & \text{ falls } a > 0 \\ \;\;0 & \text{ falls } a = 0 \\ -a & \text{ falls } a < 0 \end{cases}$

Die array-Umgebung

Die array-Umgebung kann innerhalb von Formeln verwendet werden, um eine horizontale Ausrichtung der einzelnen Formel-Elemente zu erreichen. Die Syntax ist dabei der tabular-Umgebung sehr ähnlich:

Beispiel:

\begin{align*}
    \begin{array}{lcr}
        \text{Erste Zahl}   & x         &  8 \\
        \text{Zweite Zahl}  & y         & 15 \\ \hline
        \text{Summe}        & x + y     & 23 \\
        \text{Differenz}    & x - y     & -7 \\
        \text{Produkt}      & x \cdot y & 120
    \end{array}
\end{align*}

Ergebnis:

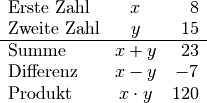
$\begin{align*} \begin{array}{lcr} \text{Erste Zahl} & x & 8 \\ \text{Zweite Zahl} & y & 15 \\ \hline \text{Summe} & x + y & 23 \\ \text{Differenz} & x - y & -7 \\ \text{Produkt} & x \cdot y & 120 \end{array} \end{align*}$

Direkt hinter \begin{align} werden in geschweiften Klammern die gewünschten Spalten-Optionen angegeben, wobei l für eine Links-Ausrichtung der Spalte, c für eine Zentrierung und r für eine Rechts-Ausrichtung steht. Die Anzahl an Spaltenoptionen muss mit der tatsächlichen Spaltenanzahl innerhalb der Tabelle übereinstimmen. In die einzelnen Felder der array-Umgebung können wiederum beliebige Formel-Elemente gesetzt werden (sogar Matrizen).

Zwischen den einzelnen Spalten-Optionen können nach Belieben |-Zeichen eingefügt werden, um (wie bei einer Tabelle) vertikale Striche zwischen den jeweiligen Spalten (oder am Rand der Tabelle) einzuzeichnen; horizontale Linien lassen sich jeweils zu Beginn einer neuen Zeile mittels der \hline-Anweisung verwirklichen.

Anmerkungen:

[1]	Anstelle mit $ ... $ können für Inline-Formeln auch mit `$ ... $` begrenzt werden. Dies wird beispielsweise vom Dokumentationssystem Sphinx für automatisch erzeugten LaTeX-Code genutzt. Anstelle mit `$$ ... $$` können eigenständige Formeln auch mit `\[ ... \]` begrenzt werden.

Inhalt

Vorheriges Thema

Nächstes Thema

Diese Seite

Mathematischer Formelsatz¶

Mathematische Symbole¶

Mathematische Ausdrücke¶