Einleitung¶
Teilbereiche der Physik¶
Die Physik kann ihrerseits in weitere Teilbereiche untergliedert werden. Hierbei unterscheidet man für gewöhnlich die „klassische“ Physik (Mechanik, Akustik, Optik und Wärmelehre) von der „modernen“ Physik. Letztere ist meist mit großem theoretischem und experimentellem Aufwand verbunden, so dass sie im Rahmen dieses Buchs nur knapp behandelt werden kann.
- Klassische Physik
Die klassische Physik ab dem 17. bis zum 19. Jahrhundert wurde stark durch Isaac Newton geprägt. Hierzu zählen unter anderem die Teilbereiche Mechanik, Akustik Optik und Wärmelehre. In diesen Bereichen sind Beobachtungen oftmals direkt mit menschlichen Sinnen möglich.
In den weiteren Teilbereichen Elektrizitätslehre und Magnetismus, die ebenfalls zur „klassischen“ Physik gezählt werden, sind viele Vorgänge trotz oft alltäglichen Erfahrungen nicht direkt mit menschlichen Sinnen wahrnehmbar.
- Moderne Physik
Durch die Arbeiten von Albert Einstein (Relativitätstheorie), Erwin Schrödinger und Werner Heisenberg (Quantentheorie) und anderen wurde im 20. Jahrhundert die „moderne“ Physik begründet.
Hierzu zählen unter anderem die Atom-, Kern- und Teilchenphysik, die Quantentheorie, die Relativitätstheorie sowie die Festkörperphysik. Direkte Beobachtungen von Vorgängen sind hierbei mit menschlichen Sinnen (meist) unmöglich; teilweise sind sehr aufwendige Experimente nötig.
Sowohl Newton als auch Einstein haben mit ihren wissenschaftlichen Arbeiten jeweils die vorherrschenden Weltbilder maßgeblich beeinflusst. Beispielsweise vertrat Newton entgegen der bis dahin vorherrschenden Meinung die Ansicht, dass die Erde sich um die Sonne bewege und nicht umgekehrt. Einstein wiederum vertrat die Ansicht, dass es kein absolutes Bezugsystem (keinen „Äther“) gebe, also nur die relative Bewegung von Objekten von Bedeutung sei; aus den daraus resultierenden Folgerungen ist unter anderem die Urknall-Theorie entstanden.
Bis heute gibt es in allen Forschungsbereichen neue Erkenntnisse. Beispielsweise haben Forscher im Jahr 2014 publiziert, dass Wasser zwei flüssige Phasen haben kann.[1] Ob dies tatsächlich so ist, welche Erklärungen hierfür gefunden werden können und welche Konsequenzen diese Erkenntnis wohl haben wird, kann bis heute niemand mit Gewissheit sagen..
Physikalisches Experimentieren¶
Um naturwissenschaftliche Zusammenhänge „mit allen Sinnen“ erfahren zu können, lassen sich zu vielen Themen gezielt Experimente durchführen. Versuche, die unter gleichen Bedingungen stets gleiche Ergebnisse liefern, bilden die Basis für das Formulieren von Gesetzmäßigkeiten und für technische Anwendungen.
In vielen Fällen laufen Experimente nach folgendem Schema ab:
- Beobachten:
Aus unseren alltäglichen Erfahrungen haben wir eine Vorstellung von Naturerscheinungen.
Beispiele:
Ein Regenbogen, ein Gewitter, das Gefrieren und Schmelzen von Wasser, das Schwimmen von Holz in Wasser, das Tönen einer Glocke, das Fallen eines Körpers… all diese Vorgänge wiederholen sich unter gleichen Bedingungen immer wieder auf die gleiche Art und Weise.
Was passiert allerdings, wenn sich einige Bedingungen ändern?
- Fragen:
Wie entsteht ein Blitz? Warum kommt ein in die Höhe geworfener Stein auf die Erde zurück? Wie funktioniert eine Glühbirne, ein Auto, oder ein Fernseher?
Wie bei einem Puzzle lassen sich viele Antworten leicht(er) finden, wenn das Wissen um die einzelnen „Bausteine“ und ihrer Zusammensetzung vorhanden ist.
- Experimentieren:
Mit Versuchen lassen sich einzelne Zusammenhänge in einer geeigneten Umgebung gezielt untersuchen. Während eines Versuchs wird sorgfältig beobachtet, gemessen und protokolliert. Die Ergebnisse eines Experiments können dann die eigene Vermutung bestätigen oder widerlegen.
In der Physik werden Zustandsänderungen von Objekten untersucht, in der Chemie Reaktionen chemischer Stoffe.
- Naturgesetz(e) formulieren:
Lassen sich physikalische Vorgänge unter gleichen Bedingungen zu jeder Zeit wiederholen, so lassen sich nach Auswertung der Ergebnisse allgemein gültige Aussagen folgender Art formulieren:
„Falls diese und jene Bedingung gegeben ist, dann wird diese und jene Wirkung eintreten!“
Die Darstellung physikalischer Gesetze (Ursache und Wirkung) kann qualitativ in Worten oder quantitativ in mathematischer Form erfolgen. Eine Darstellung in mathematischer Form ist oft aussagekräftiger, erfordert allerdings eine Messbarkeit der entsprechenden Größen.
Größen und Einheiten¶
Maßeinheiten spielen in der Physik eine wichtige Rolle:
- Jede physikalische Größe entspricht einer messbaren Eigenschaft eines Objekts oder Zustands, beispielsweise Länge, Masse, Zeit, Geschwindigkeit, Energie, Temperatur usw.
- Jede physikalische Größe setzt sich aus einem Zahlenwert und einer Maßeinheit zusammen:
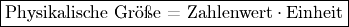
Physikalische Größen werden üblicherweise mit lateinischen oder griechischen
Buchstaben in kursiver Schrift bezeichnet, Einheiten hingegen sollten zur
optischen Unterscheidung nicht-kursiv geschrieben werden. In der
Formeldarstellung schreibt man für eine Größe  auch folgendes:
auch folgendes:
![a = \{ a \} \cdot [a]](_images/math/3126c3db46fcbd283696a25e7567d03c880c639f.png)
Handelt es sich beispielsweise bei der physikalischen Größe um die Masse
 eines Objekts, so ist
eines Objekts, so ist ![[m] = \unit{kg}](_images/math/a0cf0305b092f6b5dde213c50b4c56415c1cd47b.png) , falls die Masse in der
Einheit „Kilogramm“ angegeben wird. Wiegt das Objekt
, falls die Masse in der
Einheit „Kilogramm“ angegeben wird. Wiegt das Objekt 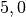 Kilogramm, so
ist für dieses Objekt
Kilogramm, so
ist für dieses Objekt 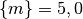 ; insgesamt kann man also in diesem
Fall
; insgesamt kann man also in diesem
Fall ![m=\unit[5,0]{kg}](_images/math/4e25c451f338a0fe6c9be7cebb63d24051505d25.png) schreiben (das Mal-Zeichen zwischen Zahlenwert und
Einheit wird üblicherweise nicht explizit geschrieben).
schreiben (das Mal-Zeichen zwischen Zahlenwert und
Einheit wird üblicherweise nicht explizit geschrieben).
- Größen können nur addiert oder subtrahiert werden, wenn sie in ihren Einheiten übereinstimmen. Zuerst müssen also einzelne Einheiten gegebenenfalls passend umgerechnet werden.
- Größen können stets miteinander multipliziert oder durcheinander dividiert werden. Das Ergebnis ergibt sich durch die Anwendung der Rechenvorschrift sowohl auf die Zahlenwerte als auch auf die Einheiten der einzelnen Größen.
Beispiele:
- Die Addition von
![\unit[1,0]{m}](_images/math/aa09fb2b807a0ab0848818db9c6c2e1844a81a80.png) plus
plus ![\unit[70]{cm}](_images/math/1f5e7d8a6bb65153dac18b9c554c7d5625f10a58.png) kann man
auch als
kann man
auch als ![\unit[1,0]{m} + \unit[0,70]{m}](_images/math/4a4224b1c87d23d23d429e53c5812a4c741bd6ea.png) schreiben; das Ergebnis ist
dann
schreiben; das Ergebnis ist
dann ![\unit[1,7]{m}](_images/math/cc95a860c90bba087b088c3224147bb514a638ca.png) .
. - Bewegt man sich um eine
![\unit[1,5]{m}](_images/math/3894017ec6f96ec977d796dee7314e9bdd6012ac.png) je
je ![\unit[1]{s}](_images/math/a69295d00e6b71b7e4e11080041344fe1df0e00c.png) weiter,
so beträgt die Geschwindigkeit
weiter,
so beträgt die Geschwindigkeit ![\unit[\frac{1,5}{1,0}]{\frac{m}{s}}=
\unit[1,5]{\frac{m}{s}}](_images/math/f7800acac028b2446290feab2bcb1d95497c10a2.png) .
. - Wirkt auf eine Kurbel eine Kraft von
![\unit[40]{N}](_images/math/e20861242c6b30b60eafcc31b715b42ac84d0724.png) im Abstand von
im Abstand von
![\unit[0,3]{m}](_images/math/5fe5ca12e8efc60162a7d4755dedd7efc1f0d7fd.png) von der Drehachse in senkrechter Richtung ein, so
bewirkt diese ein Drehmoment von
von der Drehachse in senkrechter Richtung ein, so
bewirkt diese ein Drehmoment von ![\unit[40]{N} \cdot \unit[0,3]{m} =
\unit[12]{Nm}](_images/math/68b59ac7842156717b63d10cff54456f6d4bf9d3.png) .
.
Skalare und vektorielle Größen
Manche physikalische Größen, beispielsweise Masse und Temperatur, haben keine räumliche Vorzugsrichtung, ihre Wirkung ist also in allen Richtungen des Raumes gleich. Durch die Angabe eines Zahlenwerts und der zugehörigen Maßeinheit werden solche so genannten „skalaren“ Größen hinreichend beschrieben.
Skalare Größen sind beispielsweise Masse, Temperatur, Volumen, elektrische Ladung, und andere.
Andere physikalische Größen, beispielsweise Kraft und Geschwindigkeit, besitzen stets eine eindeutige Richtung im Raum. In Zeichnungen werden derartige Größen durch Pfeile (Vektoren), in physikalischen Formeln durch einen kleinen Pfeil über dem Formelsymbol dargestellt. Im dreidimensionalen Raum sind letztlich auch drei Zahlenwerte und die zugehörige Maßeinheit nötig, um die physikalische Wirkung dieser so genannten „vektoriellen“ Größen in die jeweiligen Raumrichtungen hinreichend zu beschreiben.[2]
Vektorielle Größen sind beispielsweise Kraft, Beschleunigung, Geschwindigkeit, und andere.
Internationale Einheiten
Durch Verwendung von klar festgelegten Maßeinheiten lassen sich Messergebnisse auch zu einer anderen Zeit, an einem anderen Ort und/oder in einer anderen Sprache nachvollziehen und vergleichen.
Im Jahr 1960 wurden auf einer Fachtagung folgende sieben Einheiten als
internationales Einheitensystem festgelegt 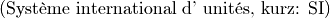 :
:
| Größe | Einheit | Einheitsbezeichnung |
| Länge | 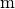 |
Meter |
| Zeit |  |
Sekunde |
| Masse | 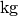 |
Kilogramm |
| Temperatur | 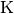 |
Kelvin |
| Elektr. Stromstärke | 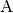 |
Ampere |
| Lichtstärke | 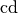 |
Candela |
| Stoffmenge | 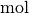 |
Mol |
Aus diesen sieben „SI-Einheiten“ lassen sich die weiteren (für die Praxis ebenso relevanten) Einheiten nur mittels Multiplikation oder Division herleiten.
Eine Übersicht zu in Deutschland und international anerkannten Einheiten und ihren Umrechnungen gibt es gratis als Broschüre (PDF) von der Physikalisch-Technischen Bundesanstalt.
Zehnerpotenzen
Je nach Untersuchungsgegenstand können sich die Zahlenwerte von Messergebnissen um etliche Größenordnungen unterscheiden – beispielsweise besitzt ein Planet eine erheblich größere Masse als ein einzelnes Atom, und ein Isolator einen um ein Vielfaches größeren elektrischen Widerstand als ein Leiter. Um dennoch die üblichen Maßeinheiten nutzen zu können – beispielsweise die Masse eines Körpers in Kilogramm anzugeben – hat man der Übersichtlichkeit halber so genannte „Zehnerpotenzen“ eingeführt. Hierbei gilt beispielsweise:
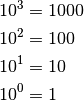
Der letzte Ausdruck 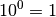 wurde willkürlich festgelegt; diese
Festlegung bringt allerdings den Vorteil mit sich, dass man die Anzahl an Nullen
des Ergebnisses unmittelbar anhand des Exponenten ablesen kann.
wurde willkürlich festgelegt; diese
Festlegung bringt allerdings den Vorteil mit sich, dass man die Anzahl an Nullen
des Ergebnisses unmittelbar anhand des Exponenten ablesen kann.
Bei der Angabe von Zehnerpotenzen sind auch negative Exponenten üblich, also beispielsweise:
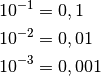
Anstelle 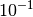 könnte man auch
könnte man auch 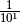 schreiben, das
Minuszeichen im Exponenten deutet somit lediglich darauf hin, dass die jeweilige
(Zehner-)Potenz im Nenner steht.[3] Die Zahl im Exponent gibt wiederum an, wie
viele Nullen im Ergebnis vorkommen; nach der ersten Null muss dabei jeweils das
Komma gesetzt werden.
schreiben, das
Minuszeichen im Exponenten deutet somit lediglich darauf hin, dass die jeweilige
(Zehner-)Potenz im Nenner steht.[3] Die Zahl im Exponent gibt wiederum an, wie
viele Nullen im Ergebnis vorkommen; nach der ersten Null muss dabei jeweils das
Komma gesetzt werden.
Für die einzelnen Zehnerpotenzen gibt es sprachliche Abkürzungen, beispielsweise
steht die Vorsilbe „kilo“ für den Faktor 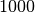 beziehungsweise
beziehungsweise
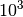 ; somit kann man beispielsweise für
; somit kann man beispielsweise für ![\unit[1000]{g}](_images/math/ccff4666a484219659ed823da2f227f17fdd4d37.png) auch
auch
![\unit[1 \cdot 10^3]{g} = \unit[1]{kg}](_images/math/a7aa3d26a7d3c65cfd08a244535a5630edeef24f.png) schreiben. Einige solcher Potenzen
sind in der folgenden Tabelle aufgelistet.
schreiben. Einige solcher Potenzen
sind in der folgenden Tabelle aufgelistet.
| Vorsilbe | Kurzzeichen | Faktor | Kurzschreibweise |
| Exa | 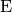 |
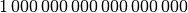 |
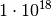 |
| Peta | 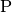 |
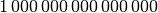 |
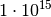 |
| Tera | 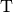 |
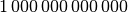 |
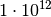 |
| Giga | 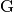 |
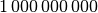 |
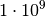 |
| Mega | 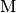 |
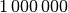 |
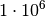 |
| Kilo | 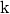 |
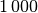 |
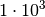 |
| Hekto | 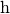 |
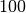 |
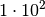 |
| Deka | 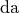 |
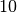 |
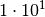 |
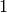 |
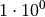 |
||
| Dezi | 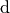 |
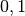 |
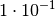 |
| Zenti |  |
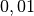 |
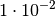 |
| Milli | 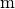 |
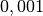 |
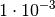 |
| Mikro | 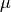 |
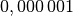 |
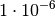 |
| Nano | 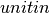 |
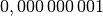 |
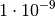 |
| Piko | 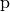 |
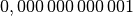 |
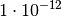 |
| Femto | 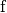 |
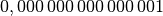 |
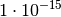 |
| Atto |  |
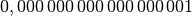 |
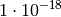 |
Ein wesentlicher Vorteil von Zehnerpotenzen liegt darin, dass sie sich aufgrund
der Beziehung 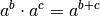 einfach miteinander
verrechnen lassen. Um beispielsweise eine Längenangabe von Dezimeter
einfach miteinander
verrechnen lassen. Um beispielsweise eine Längenangabe von Dezimeter
![(\unit{dm} = \unit[10^{-1}]{m})](_images/math/10bbca8fa8d3c0481f433fd215742b36ef7cf4c5.png) in Millimeter
in Millimeter ![(\unit{mm} =
\unit[10^{-3}]{m})](_images/math/ddf7fa1ef14dcfd748760c2619b35d948090447e.png) umzurechnen, genügt es, den jeweiligen Zahlenwert mit
umzurechnen, genügt es, den jeweiligen Zahlenwert mit
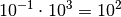 zu multiplizieren. Hierfür gibt es bei vielen
Taschenrechnern sogar eine eigene Taste, die mit
zu multiplizieren. Hierfür gibt es bei vielen
Taschenrechnern sogar eine eigene Taste, die mit 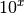 oder mit
oder mit EXP
gekennzeichnet ist, und einige Tipparbeit ersparen kann.[4] Durch die
Verwendung von Zehnerpotenzen bleibt einem auch das „Komma-Schieben“ (mitsamt
der möglichen Fehlerquelle, dass mal eine Null übersehen wird) erspart.
Ein weiterer Vorteil bei der Verwendung von Zehnerpotenzen besteht darin, dass
wegen der Beziehung 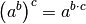 auch
Umrechnungen von quadratischen oder kubischen Einheiten leicht vorgenommen
werden können: Man ersetzt die jeweilige Vorsilbe durch die jeweilige
Zehnerpotenz, und potenziert anschließend sowohl wie Einheit wie auch den
Vorfaktor.
auch
Umrechnungen von quadratischen oder kubischen Einheiten leicht vorgenommen
werden können: Man ersetzt die jeweilige Vorsilbe durch die jeweilige
Zehnerpotenz, und potenziert anschließend sowohl wie Einheit wie auch den
Vorfaktor.
Beispiele:
Wie viele Quadrat-Millimeter entsprechen einem Quadrat-Meter?
Für die Umrechnung zwischen
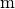 und
und 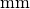 gilt:
gilt:![\unit[1]{m} = \unit[1 \cdot 10^3]{mm}](_images/math/749a71bf5e6e6e1b8ef9ccf543cd5fd2d5f059ac.png)
Somit gilt für einen Quadrat-Meter:
![\left(\unit[1]{m}\right)^2 = 1 \cdot \left(\unit[10^3]{mm} \right)^2 =
\unit[1\cdot \left(10^3\right)^2 ]{mm^2} = 1 \cdot \unit[10^6]{mm^2}](_images/math/d86392032e37be8903299b016f4ccb5b59d70a83.png)
Bei der Umwandlung wurd zunächst die umzurechnende Einheit in Klammern gesetzt und die Zehner-Vorsilbe durch die entsprechende Zehnerpotenz ersetzt; anschließend wurden sowohl die Zehnerpotenz wie auch die Einheit quadriert.
Welcher Bruchteil eines Kubik-Meters ist ein Kubik-Zentimeter?
Für die Umrechnung zwischen
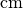 und
und 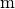 gilt:
gilt:![\unit[1]{cm} = \unit[1 \cdot 10^{-2}]{m}](_images/math/c4fa43034f438b654889a5c20e9a6e3718124973.png)
Somit gilt für einen Kubik-Meter:
![\left(\unit[1]{cm} \right)^3 = \left(\unit[10^{-2}]{m} \right)^3 =
\unit[1 \cdot \left(10^{-2}\right)^3]{m^3} = \unit[1 \cdot 10^{-6}]{m^3}](_images/math/8b597ab79fe41e2c89902e7cf49aa3c2b4690525.png)
Die Umrechnung in der jeweils anderen Richtung funktioniert ebenso; der „Umrechnungsfaktor“ bleibt gleich, der Exponent der Zehnerpotenz hat dann lediglich ein umgekehrtes Vorzeichen.
Messfehler
Physikalische Messungen erfolgen durch ein Vergleichen der zu messenden Größe mit einer in der entsprechenden Einheit geeichten Skala (Meterstab, Waage, Thermometer, Volt- und Amperemeter, usw). Häufig werden elektrische Messverfahren angewendet, welche die Messergebnisse mittels digitaler Anzeigen einfach ablesbar machen.
Dennoch muss stets beachtet werden, dass die ermittelten Messwerte fehlerhaft sein können. Man unterscheidet prinzipiell zwischen systematischen und zufälligen („statistischen“) Messfehlern:
Systematische Fehler ergeben sich aus einer falsch eingestellten Messapparatur. Ist beispielsweise ein Thermometer falsch kalibriert, so weicht die angezeigte Temperatur unweigerlich von der tatsächlichen Temperatur ab.
Systematische Fehler treten bei jeder wiederholten Messung erneut auf, oftmals sorgen sie für eine konstante Abweichung vom tatsächlichen Wert (wenn beispielsweise die Skala eines Lineal bei
![\unit[1]{mm}](_images/math/d96fa97c6d890bf9efd0b11602b0de8767afb6d5.png) statt
statt
![\unit[0]{mm}](_images/math/3cfaaf905e7fb3329d8114f1f0c0eaaac5a3c6dc.png) beginnt).
beginnt).Statistische Fehler lassen sich auf Schwankungen der zu messenden Größe bei punktuellen Messungen mit Messfühlern, Messverzögerungen sowie Ablese-Ungenauigkeiten (bei nicht-digitalen Anzeigen) beziehungsweise ungenaue elektronische Sensoren (bei digitalen Messgeräten) zurückführen.
Für jede einzelne Messung gilt also:

oder kürzer:

Eine derartige explizite Darstellung eines Messergebnisses stellt letztlich eine
Wahrscheinlichkeitsaussage dar. Üblicherweise wird damit gemeint, dass sich der
tatsächliche Wert mit einer Wahrscheinlichkeit von 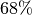 innerhalb des
Intervalls
innerhalb des
Intervalls ![[\text{Messwert} - \text{Fehler};\; \text{Messwert} +
\text{Fehler}]](_images/math/b5dff279b4d2129bc241b4df6f9377c6fd00a046.png) befindet.
befindet.
Systematische Fehler treten bei jeder Messung erneut auf; sie können durch geschickte experimentelle Methoden minimiert und teilweise sogar komplett vermieden werden. Zufällige Fehler lassen sich nie komplett vermeiden; man versucht sie durch wiederholte Messungen und statistische Methoden möglichst gering zu halten.
Anmerkungen:
| [1] | Die Original-Mitteilung (en.) stammt von einem Forscher-Team der Universität Utrecht, der zugehörige Artikel ist im renommierten Nature-Magazin erschienen. |
| [2] | Bisweilen wird die Zeit als „vierte Komponente“ einer vektoriellen Größe auch der zeitliche Verlauf mit berücksichtigt; man kann das Ergebnis dann nicht mehr als einzelnes „Bild“ in einem dreidimensionalen Koordinatensystem vorstellen, sondern vielmehr als „Film“ einer Vielzahl solcher aufeinander folgender Bilder. |
| [3] | Auch bei Einheiten wird bisweilen diese Schreibweise genutzt, also
beispielsweise 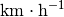 anstelle von anstelle von 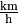 geschrieben. Der Vorteil dieser Schreibweise bei Einheiten liegt darin, dass
man somit keine „gequetschten“ Brüche in den Fließtext (oder in eine
Tabellenzeile) einfügen muss.
geschrieben. Der Vorteil dieser Schreibweise bei Einheiten liegt darin, dass
man somit keine „gequetschten“ Brüche in den Fließtext (oder in eine
Tabellenzeile) einfügen muss. |
| [4] | Die bisweilen anzutreffende Tasten-Bezeichnung EXP ist eine
Kurzschreibweise für „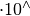 “. In noch kürzerer
Form wird diese Schreibweise auch in Programmiersprachen verwendet;
beispielsweise kann in Python die Zahl “. In noch kürzerer
Form wird diese Schreibweise auch in Programmiersprachen verwendet;
beispielsweise kann in Python die Zahl 1500 auch
als 1.5e3 eingegeben werden. |
