Regelmäßige Vielecke¶
Ein  -Eck, bei dem alle Seiten gleich lang und alle Innen-
beziehungsweise Außenwinkel gleich groß sind, wird regelmäßige Vieleck genannt.
-Eck, bei dem alle Seiten gleich lang und alle Innen-
beziehungsweise Außenwinkel gleich groß sind, wird regelmäßige Vieleck genannt.
Regelmäßige Vielecke haben folgende Eigenschaften:
- Jedes regelmäßige
 -Eck hat jeweils
-Eck hat jeweils  Ecken,
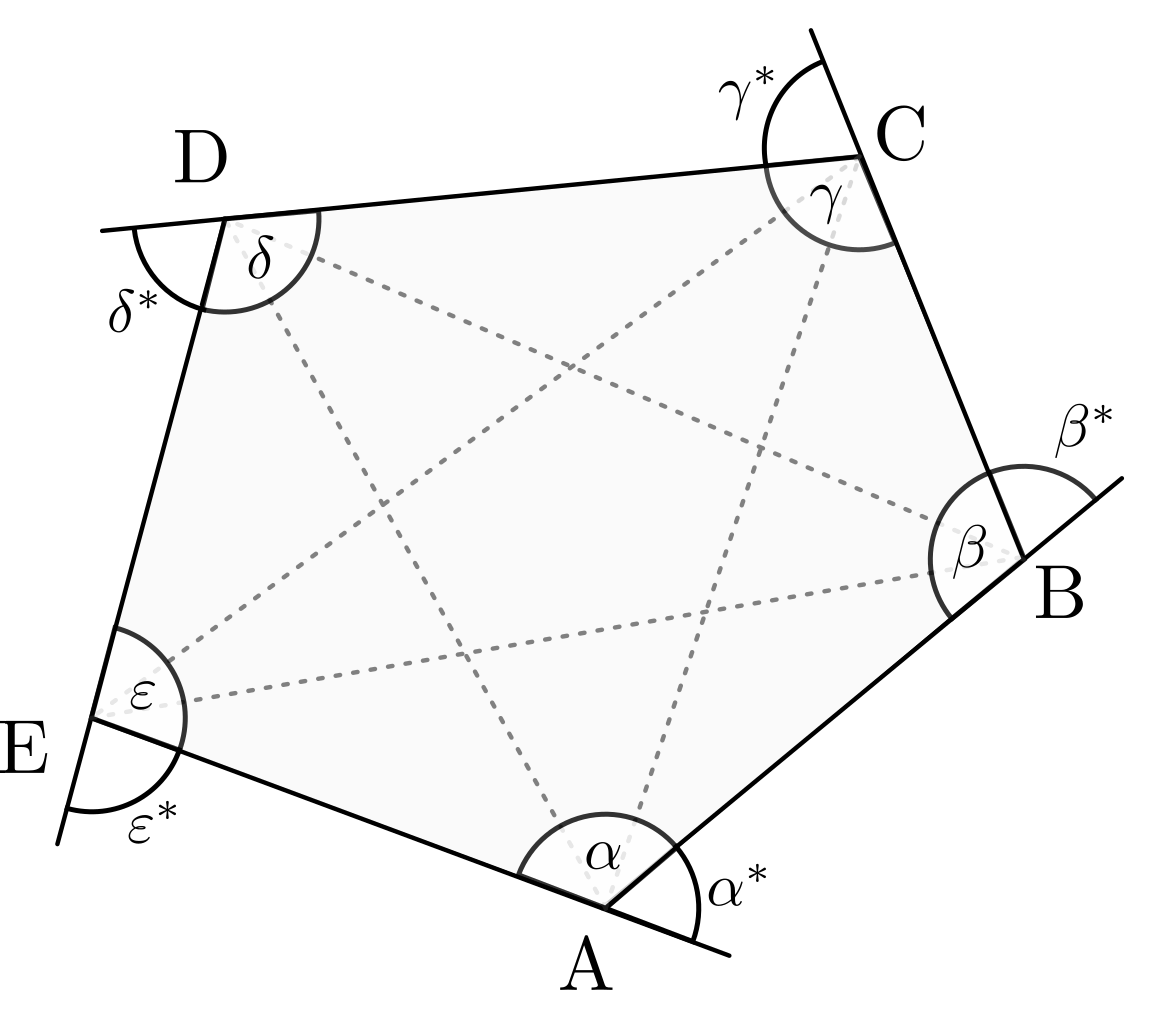
Ecken,  Seiten,
Seiten,
 Innen- beziehungsweise Außenwinkel sowie
Innen- beziehungsweise Außenwinkel sowie 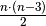 Diagonalen.
Diagonalen. - Jedes regelmäßige
 -Eck ist
-Eck ist  -fach punktsymmetrisch.
-fach punktsymmetrisch. - Um jedes regelmäßige
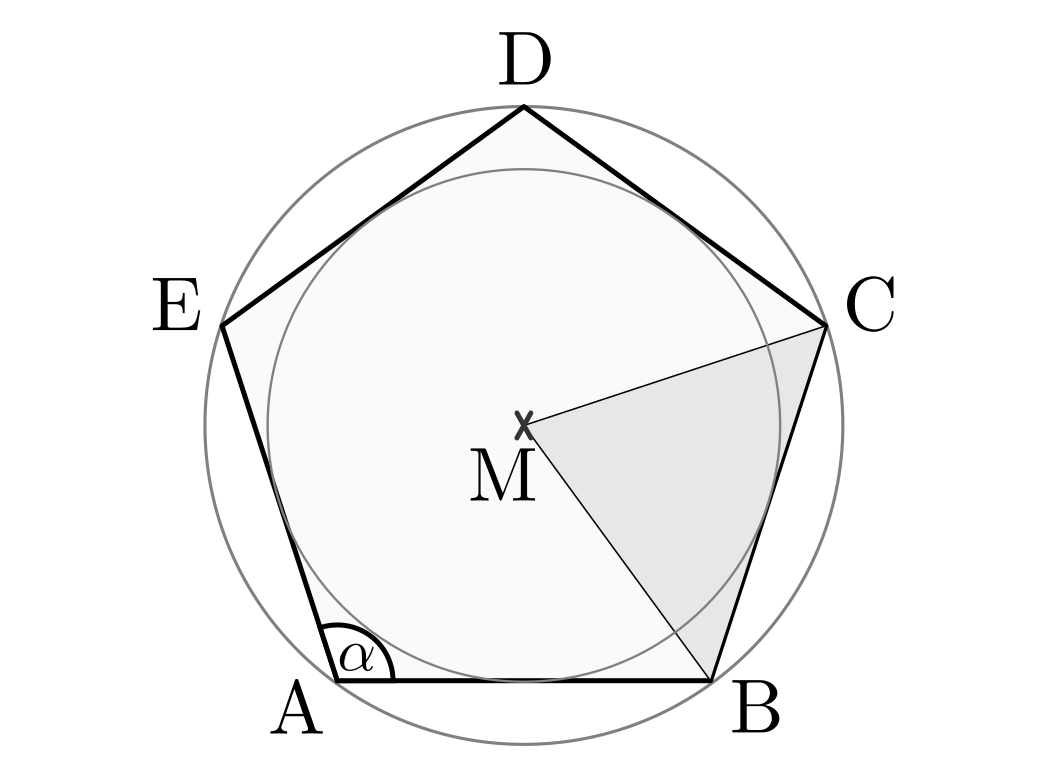
 -Eck lässt sich ein Kreis zeichnen, der durch
alle Ecken verläuft; diesen bezeichnet man als Umkreis.
-Eck lässt sich ein Kreis zeichnen, der durch
alle Ecken verläuft; diesen bezeichnet man als Umkreis. - In jedes regelmäßige
 -Eck lässt sich ein Kreis zeichnen, der alle
Seitenmitten berührt; diesen bezeichnet man als Inkreis.
-Eck lässt sich ein Kreis zeichnen, der alle
Seitenmitten berührt; diesen bezeichnet man als Inkreis. - Das gemeinsame Zentrum von Um- und Inkreis ist der Mittelpunkt des Vielecks.
- Verbindet man den Mittelpunkt mit den Ecken, so erhält man
 kongruente, gleichschenklige Dreiecke; diese werden auch „Bestimmungsdreiecke“
genannt.
kongruente, gleichschenklige Dreiecke; diese werden auch „Bestimmungsdreiecke“
genannt. - Jeder Innenwinkel eines regelmäßigen
 -Ecks beträgt
-Ecks beträgt
![\frac{n-2}{n} \cdot \unit[180]{\degree}](../../_images/math/47fb248c891f3b5a5a049186aec1fdf0afed7d27.png) .
. - Jeder Außenwinkel eines regelmäßigen
 -Ecks beträgt
-Ecks beträgt
![\frac{\unit[360]{\degree}}{n}](../../_images/math/db7f40172b694d4138620da6d7a210466c65097d.png) .
.
Bezeichnet die Seitenlänge mit  , den Radius des Inkreises mit
, den Radius des Inkreises mit
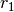 und den Radius des Umkreises mit
und den Radius des Umkreises mit 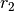 , so gilt für den Umfang
und die Fläche eines regelmäßigen
, so gilt für den Umfang
und die Fläche eines regelmäßigen  -Ecks:
-Ecks:
![\text{Fl\"ache} &= \frac{n}{2} \cdot s \cdot r_1 = \frac{n}{2} \cdot s \cdot
\sqrt{r_2^2 - \frac{s^2}{4}} \\[10pt]
\text{Umfang} &= n \cdot s](../../_images/math/04b70be5887c2fa19c4a1a5cdfa1caed4b49aa0c.png)
Beliebige (auch nicht regelmäßige) Vielecke haben zudem allgemein folgende Eigenschaften:
- Die Summe der Innenwinkel eines
 -Ecks beträgt
-Ecks beträgt ![(n-2) \cdot
\unit[180]{\degree}](../../_images/math/e562fcbddccd735b72b83a450fe597f936457b07.png) .
. - Die Summe der Außenwinkel eines
 -Ecks beträgt stets
-Ecks beträgt stets ![\unit[360]{\degree}](../../_images/math/2c253b7aac58187436afbabfadbfc9918aa9eabe.png) .
. - Ein Innenwinkel und sein zugehöriger Außenwinkel betragen in Summe stets
![\unit[180]{\degree}](../../_images/math/a62139d45d177455d34d6e27e1030722257dea2f.png) (da es sich um Nebenwinkel handelt).
(da es sich um Nebenwinkel handelt). - Die Winkelhalbierenden eines Innenwinkels und die des zugehörigen Außenwinkels sind zueinander stets senkrecht.
Per Festlegung haben  -Ecke zudem keine nach innen zeigenden Ecken sowie
keine einander schneidenden Seiten.
-Ecke zudem keine nach innen zeigenden Ecken sowie
keine einander schneidenden Seiten.