Kreis und Ellipse¶
Der Kreis¶
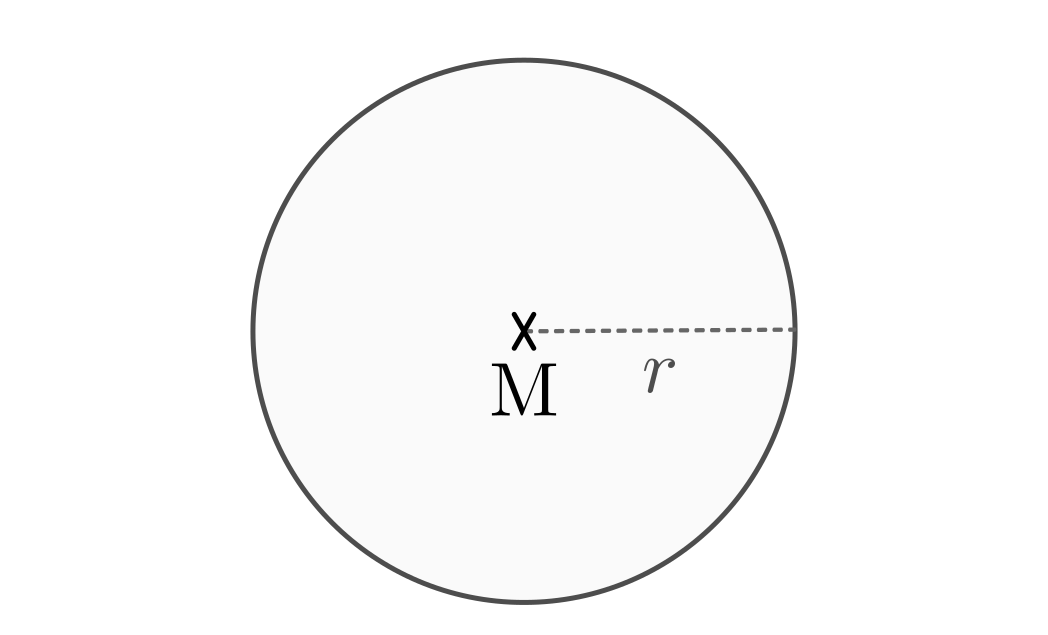
Jeder Kreis besitzt als Besonderheit, dass alle Punkte auf der Kreislinie gleich
weit vom Mittelpunkt 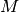 entfernt liegen.
entfernt liegen.
Für den Umfang und die Fläche eines Kreises mit Radius  gilt:
gilt:
(1)¶![\text{Umfang} &= 2 \cdot \pi \cdot r \\[4pt]
\text{Fl\"ache} &= \pi \cdot r^2](../../_images/math/2fdacc1a62590a757141c623bdcb19381041a3be.png)
Dabei wird 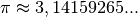 als „Kreiszahl“ bezeichnet.
als „Kreiszahl“ bezeichnet.
Der Kreisbogen¶
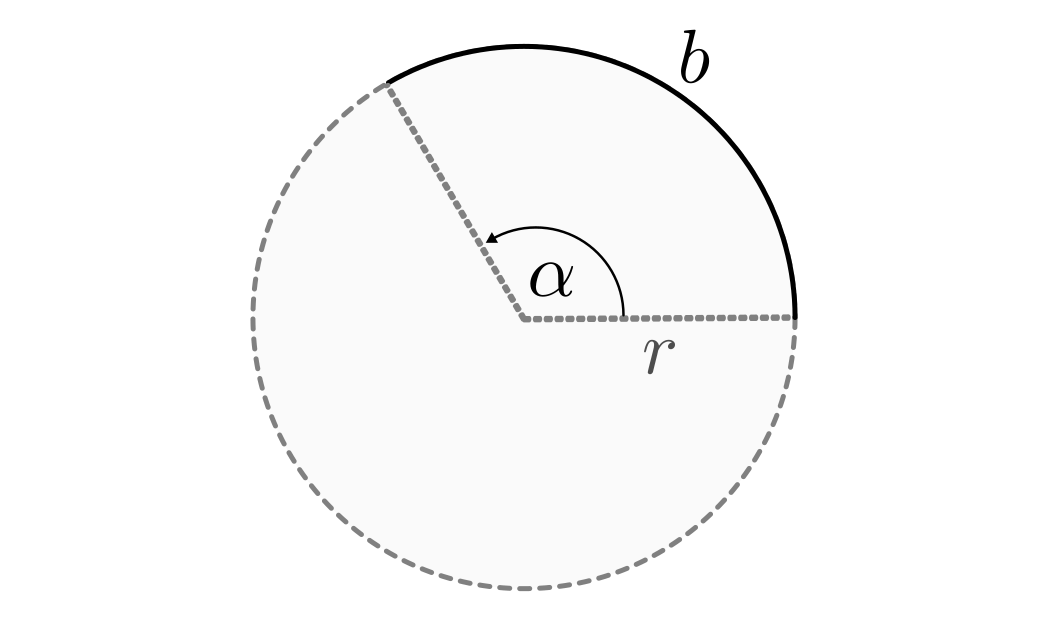
Wird anstelle eines ganzen Kreises nur ein Teil der Kreislinie gezeichnet, so bezeichnet man den entsprechenden Kreisteil als Kreisbogen.
Die Länge eines Kreisbogens hängt vom Umfang des entsprechenden Kreises ab und
davon, welchen Anteil des gesamten Kreises der Kreisbogen ausmacht. Dieser
Anteil wird durch den Mittelpunktswinkel 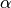 beschrieben, wobei
beschrieben, wobei
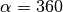 einer vollen Umdrehung entspricht. Gilt
einer vollen Umdrehung entspricht. Gilt 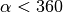 , so steht die Kreisbogenlänge
, so steht die Kreisbogenlänge  im gleichen Verhältnis zum Umfang
im gleichen Verhältnis zum Umfang
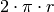 des ganzen Kreises wie
des ganzen Kreises wie 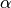 zu
zu
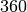 :
:
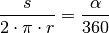
Nach dieser Gleichung, aufgelöst nach  , ergibt sich für die Länge
des Kreisbogens:
, ergibt sich für die Länge
des Kreisbogens:
(2)¶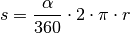
Gradmaß und Bogenma߶
Der Mittelpunktswinkel 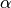 eines Kreisbogens wird gewöhnlich im
Gradmaß angegeben.
eines Kreisbogens wird gewöhnlich im
Gradmaß angegeben. 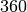 entsprechen dabei dem vollen Kreisumfang.
Betrachtet man einen Einheitskreis (Radius
entsprechen dabei dem vollen Kreisumfang.
Betrachtet man einen Einheitskreis (Radius 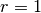 ), so hat in diesem Fall
der Kreisumfang beziehungsweise ein geschlossener Kreisbogen eine Länge von
), so hat in diesem Fall
der Kreisumfang beziehungsweise ein geschlossener Kreisbogen eine Länge von
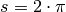 . Damit kann der Mittelpunktswinkel
. Damit kann der Mittelpunktswinkel 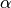 auch
durch die Länge
auch
durch die Länge  des Kreisbogens angegeben werden, wobei
des Kreisbogens angegeben werden, wobei 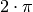 dem vollen Kreisumfang entspricht.
dem vollen Kreisumfang entspricht.
Für einen Einheitskreis kann folgende „Umrechnung“ zwischen dem Gradmaß und dem Bogenmaß verwendet werden:
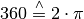
Um einen Winkel vom Gradmaß ins Bogenmaß umzurechnen, wird dieser durch
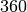 geteilt und mit
geteilt und mit 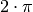 multipliziert. Im umgekehrten
Fall lässt sich ein Winkel vom Bogenmaß ins Gradmaß umrechnen, indem er durch
multipliziert. Im umgekehrten
Fall lässt sich ein Winkel vom Bogenmaß ins Gradmaß umrechnen, indem er durch
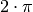 geteilt und mit
geteilt und mit 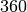 multipliziert wird.[1]
multipliziert wird.[1]
Die Grundeinheit 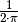 des Bogenmaßes wird auch als
„Radiant“
des Bogenmaßes wird auch als
„Radiant“ ![(\unit[1]{rad})](../../_images/math/bffb858750bf50774ac2b5451c510571f2d2d7d8.png) bezeichnet. Ein Radiant entspricht ungefähr
einem Winkelmaß von
bezeichnet. Ein Radiant entspricht ungefähr
einem Winkelmaß von 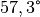 .
.
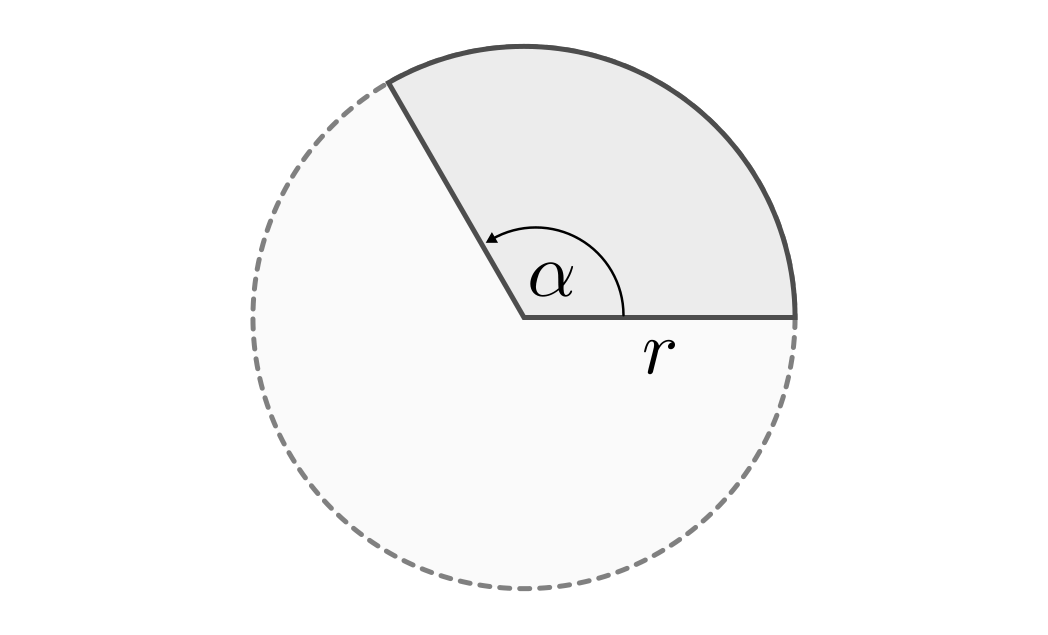
Der Kreissektor¶
Verbindet man einen Kreisbogen mit dem Mittelpunkt, so ergibt sich eine Fläche in Form eines Tortenstücks. Mathematisch wird diese Fläche als Kreissektor bezeichnet.
Der Flächeninhalt eines Kreissektors entspricht – analog zum Kreisbogen – dem
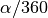 -sten Anteil der Gesamt-Kreisfläche
-sten Anteil der Gesamt-Kreisfläche 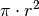 :
:
![\text{Fl\"ache des Kreissektors} &= \frac{\alpha }{\unit[360]{\degree}}
\cdot \pi \cdot r^2](../../_images/math/c64ec27b73c3d3ba46f1b7076b20f2a7892a6754.png)
Sehnen und Tangenten¶
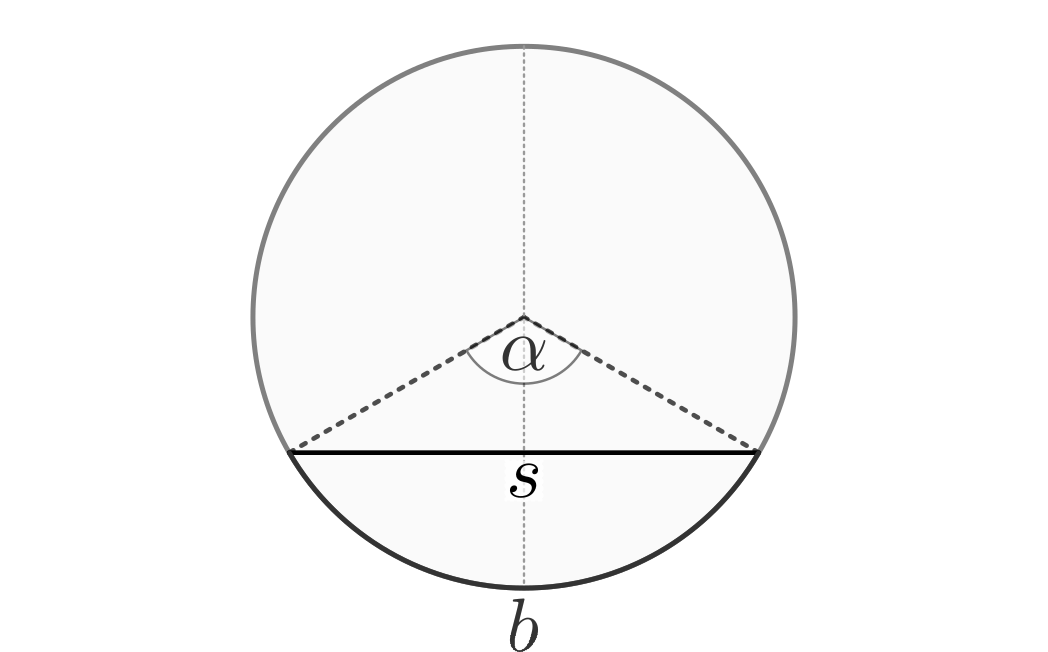
Als Kreissehne bezeichnet man eine Strecke, die zwischen zwei auf einem Kreis liegenden Punkten verläuft. Jede Kreissehne (mit Ausnahme des Durchmessers) unterteilt den Kreis in zwei verschieden große Kreisbögen; den kleineren von beiden nennt man den zur Sehne gehörenden Kreisbogen. Der Winkel zwischen dem Mittelpunkt und den beiden Endpunkten einer Sehne heißt Zentriwinkel.
Kreissehnen bringen folgende Eigenschaften mit sich:
Die durch den Mittelpunkt des Kreises und den Mittelpunkt der Sehne verlaufende Gerade halbiert die beiden Kreisbögen und den Zentriwinkel; sie ist Symmetrieachse des Dreiecks, das aus den Endpunkten der Sehne und dem Kreismittelpunkt gebildet wird.
Sind zwei Sehnen gleich lang, so sind aufgrund der Punktsymmetrie des Kreises auch die zugehörigen Kreisbögen, Zentriwinkel und Kreissektoren gleich groß.
Sind zwei Sehnen unterschiedlich lang, so gehört zur größeren Sehne der größere Kreisbogen sowie der größere Zentriwinkel.
Verschiebt man eine Sekante parallel, bis sie den Kreis nur noch in einem einzigen Punkt berührt, so spricht man von einer Tangente. Jede Tangente steht senkrecht auf der zum Berührpunkt gehörenden Radius-Linie.
Kreiswinkel¶
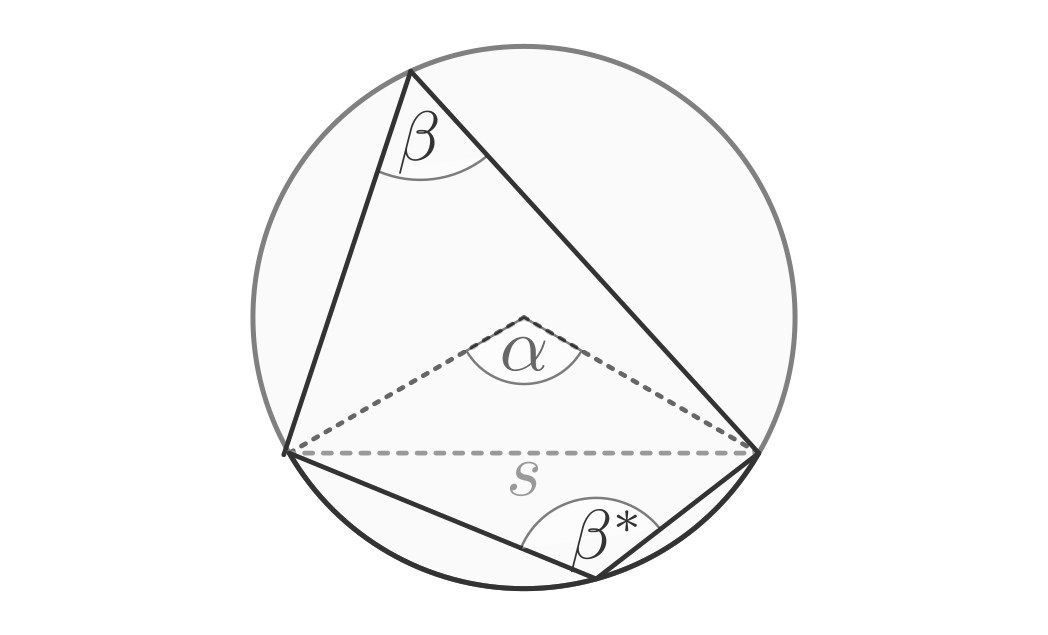
Jeder Sehne beziehungsweise jedem Kreisbogen kann eindeutig ein Zentriwinkel zugeordnet werden. Verbindet man die Endpunkte der Sehne mit einem beliebigen Punkt, der auf dem „entfernten“ (großen) Kreisbogen liegt, so erhält man so genannte „Peripherie-Winkel“. Diese Peripherie-Winkel eines Kreisbogens sind allesamt gleich groß; betraglich sind sie halb so groß wie der zum Kreisbogen gehörende Zentriwinkel:
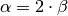
Gehören zwei Peripheriewinkel eines Kreises zur selben Sehne, aber zu
verschiedenen Kreisbögen, so beträgt die Summe beider Winkel ![\beta +
\beta^{*} = \unit[180]{\degree}](../../_images/math/66c1326392322d6ce6b5e3a430562c4a5b792650.png) . Jede Viereck, das auf diese Weise gebildet
wird (dessen vier Ecken also auf einem gemeinsamen Umkreis liegen) nennt man
„Sehnenviereck“; in einem solchen beträgt die Summe der jeweils gegenüber
liegenden Winkel je
. Jede Viereck, das auf diese Weise gebildet
wird (dessen vier Ecken also auf einem gemeinsamen Umkreis liegen) nennt man
„Sehnenviereck“; in einem solchen beträgt die Summe der jeweils gegenüber
liegenden Winkel je ![\unit[180]{\degree}](../../_images/math/a62139d45d177455d34d6e27e1030722257dea2f.png)
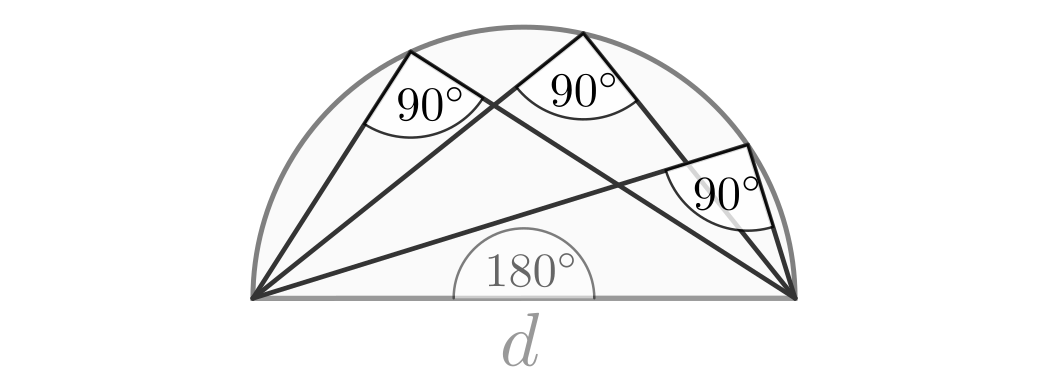
Der Satz des Thales
Beträgt der Zentriwinkel eines Kreisbogens ![\unit[180]{\degree}](../../_images/math/a62139d45d177455d34d6e27e1030722257dea2f.png) (was bei
jedem Halbkreis der Fall ist), so haben sämtliche Peripheriewinkel des einen
Betrag von
(was bei
jedem Halbkreis der Fall ist), so haben sämtliche Peripheriewinkel des einen
Betrag von ![\unit[90]{\degree}](../../_images/math/ed42da9b82869c64cf4a98987530ceace4d59e0e.png) ; sie sind also rechte Winkel.
; sie sind also rechte Winkel.
Anmerkungen:
| [1] | Gilt für den Radius eines Kreisbogens 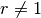 , so muss bei der
Umrechnung des Mittelpunktswinkels , so muss bei der
Umrechnung des Mittelpunktswinkels 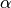 vom Grad- ins Bogenmaß die
Länge des Kreisbogens vom Grad- ins Bogenmaß die
Länge des Kreisbogens  mit dem Radius mit dem Radius  multipliziert
werden. Umgekehrt ist bei der Umrechnung des Mittelpunktswinkels vom
Bogenmaß ins Gradmaß die Kreisbogenlänge multipliziert
werden. Umgekehrt ist bei der Umrechnung des Mittelpunktswinkels vom
Bogenmaß ins Gradmaß die Kreisbogenlänge  durch den Radius durch den Radius
 zu dividieren. zu dividieren. |

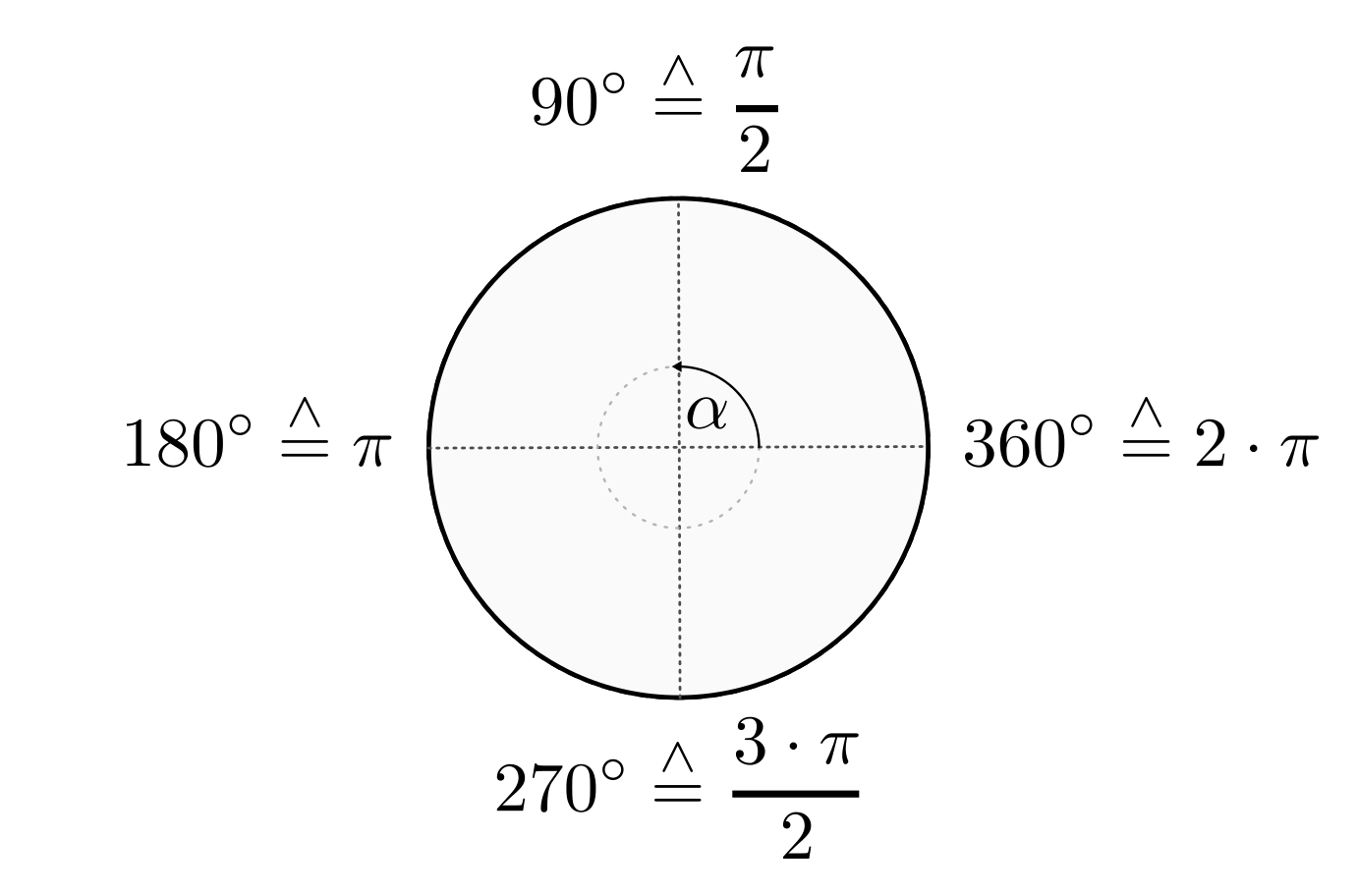
 .
.