Differentialrechnung¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Differentialrechnung.
Differenzierbarkeit setzt Stetigkeit voraus, jede an einer Stelle
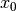 differenzierbare Funktion ist somit an dieser Stelle auch stetig.
differenzierbare Funktion ist somit an dieser Stelle auch stetig.Die Umkehrung gilt jedoch nicht: Beispielsweise ist die Funktion
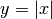 an der Stelle
an der Stelle 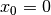 zwar stetig (weil der linksseitige und rechtsseitige
Grenzwert sowie der Funktionswert an dieser Stelle übereinstimmen), aber nicht
differenzierbar (weil die Steigungen unmittelbar links und rechts von
zwar stetig (weil der linksseitige und rechtsseitige
Grenzwert sowie der Funktionswert an dieser Stelle übereinstimmen), aber nicht
differenzierbar (weil die Steigungen unmittelbar links und rechts von
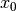 nicht übereinstimmen).
nicht übereinstimmen).
Die Ableitung der Funktion
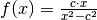 mit
mit
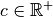 kann mittels der Quotientenregel bestimmt werden.
Mit
kann mittels der Quotientenregel bestimmt werden.
Mit 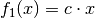 und
und 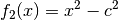 gilt:
gilt:![\left(\frac{f_1(x)}{f_2(x)} \right)' &= \frac{f_1'(x) \cdot f_2(x) -
f_1(x) \cdot f_2'(x)}{\big(f_2(x)\big)^2} \\[4pt] &= \frac{(c \cdot 1)
\cdot (x^2 - c^2) - c \cdot x \cdot (2 \cdot x - 0)}{(x^2 - c^2)^2}
\\[4pt]
&= \frac{c \cdot x^2 - c^3 - 2 \cdot c \cdot x^2 }{(x^2 - c^2)^2} =
\frac{-c \cdot x^2 - c^3}{(x^2 - c^2)^2} = \frac{-c \cdot (x^2 +
c^2)}{(x^2 - c^2)^2}](../../_images/math/2eb26dbde5966732661be9245c8353b4b174a932.png)
