Reihen- und Parallelschaltungen¶
Im folgenden wird behandelt, welche Auswirkungen sich durch eine Reihen- oder Parallelschaltung mehrerer Widerstände, Stromquellen oder Kondensatoren ergeben.
Reihen- und Parallelschaltung von Widerständen¶
In (fast) jedem Stromkreis befinden sich mehrere Verbraucher, also elektrische Widerstände. Wie diese in ihrer Gesamtheit wirken, hängt davon ab, ob sie parallel oder in Reihe geschaltet sind.
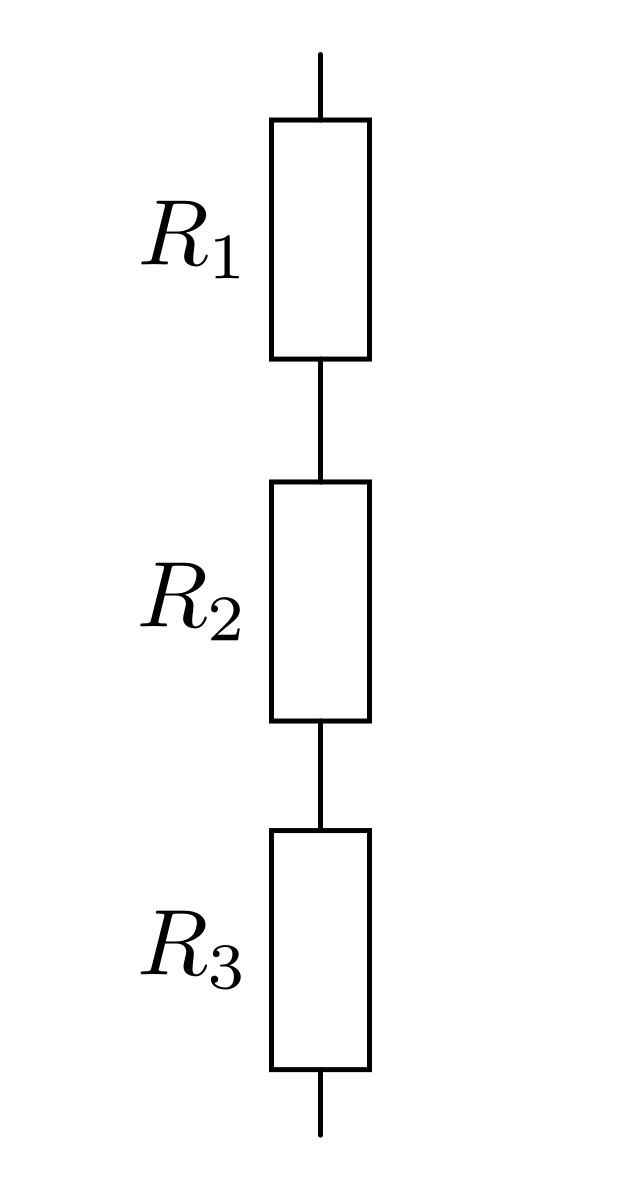
Reihenschaltung von Widerständen
Bei einer Reihenschaltung von 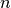 Widerständen ist der Gesamtwiderstand
Widerständen ist der Gesamtwiderstand
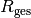 gleich der Summe der Einzelwiderstände
gleich der Summe der Einzelwiderstände 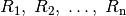 :
:
(1)¶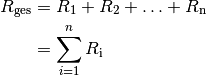
Werden beispielsweise drei Widerstände der Größe ![R = \unit[100]{\Omega }](../_images/math/c5a0c3704805185d8bb0d3ffa4fe61b5a08f412d.png) in Reihe geschaltet, so wirken sie zusammen wie ein Widerstand der Größe
in Reihe geschaltet, so wirken sie zusammen wie ein Widerstand der Größe
![R_{\mathrm{ges}} = \unit[100]{\Omega} + \unit[100]{\Omega} +
\unit[100]{\Omega} = \unit[300]{\Omega}](../_images/math/5f73bd2e873a09bd9694204ca3007652e65f9836.png) .
.
Die an einer Reihenschaltung anliegende Gesamtspannung 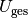 teilt sich gemäß der Maschenregel in
teilt sich gemäß der Maschenregel in 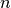 Teilspannungen
Teilspannungen 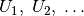 auf. Dabei ist die Gesamtspannung
gleich der Summe der einzelnen Teilspannungen:
auf. Dabei ist die Gesamtspannung
gleich der Summe der einzelnen Teilspannungen:
(2)¶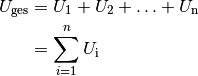
Die Stromstärke 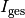 , die mehrere in Reihe geschaltete
Widerstände durchfließt, ist an allen Stellen der Reihenschaltung gleich. Somit
gilt:
, die mehrere in Reihe geschaltete
Widerstände durchfließt, ist an allen Stellen der Reihenschaltung gleich. Somit
gilt:
(3)¶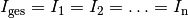
Diese Tatsache wird unter anderem zur Stromstärkemessung genutzt, indem ein Amperemeter an einer beliebigen Stelle in den zu untersuchenden (Teil-)Stromkreis als Reihenschaltung eingefügt wird.
Ist der Widerstandswert 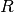 eines Widerstands einer Reihenschaltung
bekannt, kann mit Hilfe der obigen Formeln und des Ohmschen Gesetzes auf die am Widerstand anliegende Spannung
eines Widerstands einer Reihenschaltung
bekannt, kann mit Hilfe der obigen Formeln und des Ohmschen Gesetzes auf die am Widerstand anliegende Spannung 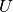 beziehungsweise auf die durch den Widerstand fließende Stromstärke
beziehungsweise auf die durch den Widerstand fließende Stromstärke 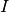 geschlossen werden:
geschlossen werden:
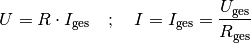
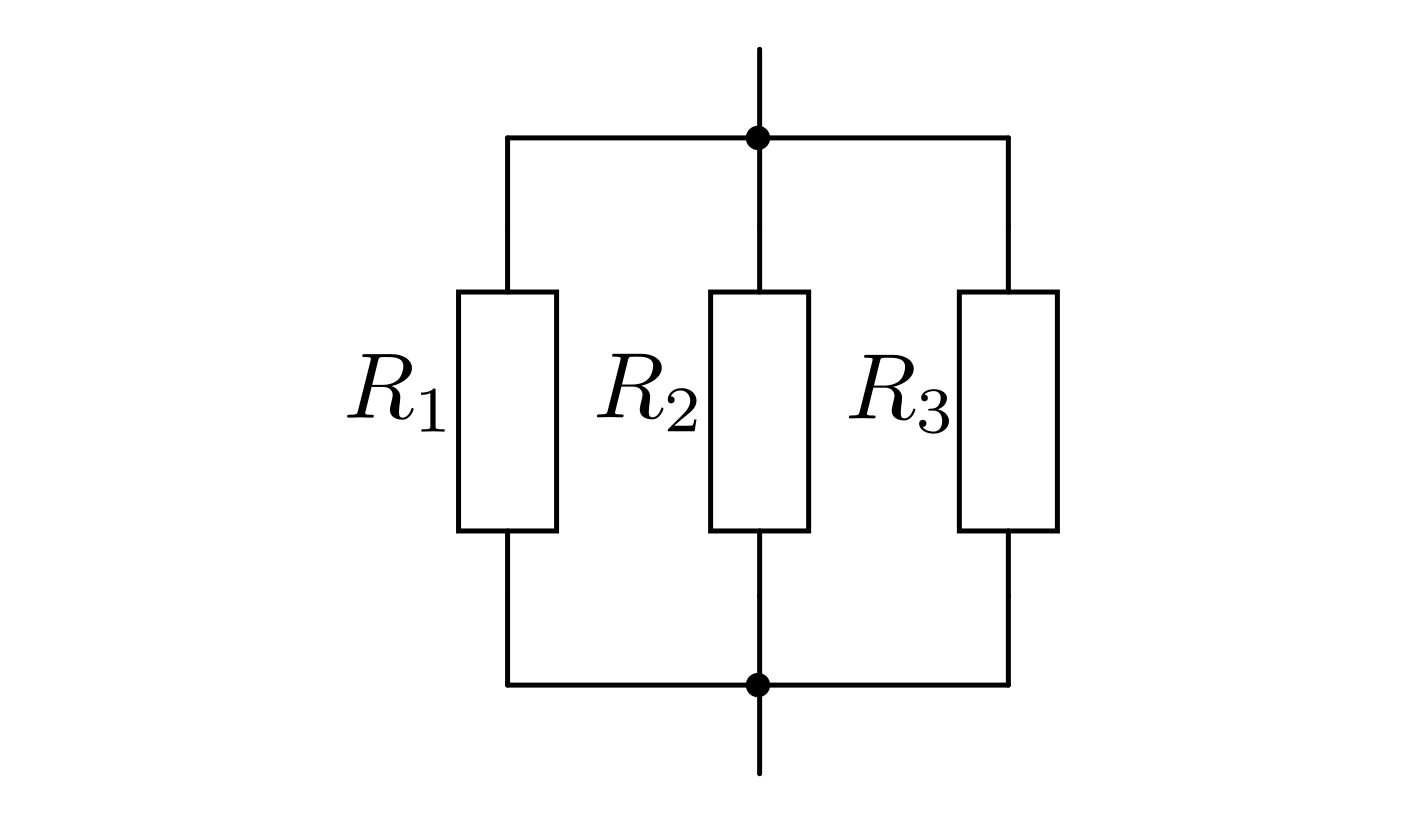
Parallelschaltung von Widerständen
Bei einer Parallelschaltung von 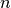 Widerständen addieren sich die
Kehrwerte der Einzelwiderstände
Widerständen addieren sich die
Kehrwerte der Einzelwiderstände 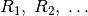 zum Kehrwert des
Gesamtwiderstandes
zum Kehrwert des
Gesamtwiderstandes 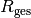 auf:
auf:
(4)¶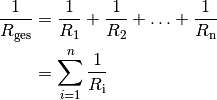
Werden beispielsweise drei Widerstände der Größe ![R = \unit[100]{\Omega}](../_images/math/7cdee5888010b1c33a53d5b8a7cbdc1ebd21a699.png) parallel zueinander geschaltet, so ergibt sich für den Kehrwert des
Gesamtwiderstands
parallel zueinander geschaltet, so ergibt sich für den Kehrwert des
Gesamtwiderstands ![\frac{1}{R_{\mathrm{ges}}} =
\unit[\frac{1}{100}]{\Omega} + \unit[\frac{1}{100}]{\Omega} +
\unit[\frac{1}{100}]{\Omega} = \unit[\frac{3}{100} ]{\Omega }](../_images/math/4224e503ad8289b9255742151e0f940638dd8f7f.png) . Der
Gesamtwiderstand beträgt somit
. Der
Gesamtwiderstand beträgt somit ![R_{\mathrm{ges}} =
\unit[\frac{100}{3}]{\Omega} \approx \unit[33,3]{\Omega}](../_images/math/da491dafc2ded7515bb5da07b9673704fcbabc43.png) .
.
An allen  Widerständen einer Parallelschaltung liegt die gleiche
Spannung an. Diese ist gleich der Gesamtspannung
Widerständen einer Parallelschaltung liegt die gleiche
Spannung an. Diese ist gleich der Gesamtspannung 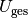 :
:
(5)¶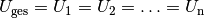
Diese Tatsache wird unter anderm zur Spannungsmessung genutzt, indem ein Voltmeter parallel zum untersuchten (Teil-)Stromkreis beziehungsweise Bauteil geschalten wird.
Die Stromstärke 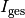 teilt sich bei einer Parallelschaltung
gemäß der Knotenregel auf
teilt sich bei einer Parallelschaltung
gemäß der Knotenregel auf 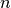 Teilstromstärken
auf:
Teilstromstärken
auf:
(6)¶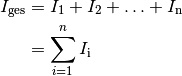
Ist der Widerstandswert 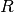 eines Widerstands einer Parallelschaltung
bekannt, kann wiederum mit Hilfe der obigen Formeln und des Ohmschen
Gesetzes auf die am Widerstand anliegende Spannung
eines Widerstands einer Parallelschaltung
bekannt, kann wiederum mit Hilfe der obigen Formeln und des Ohmschen
Gesetzes auf die am Widerstand anliegende Spannung 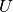 beziehungsweise auf die durch den Widerstand fließende Stromstärke
beziehungsweise auf die durch den Widerstand fließende Stromstärke 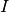 geschlossen werden:
geschlossen werden:
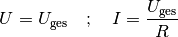
Reihen- und Parallelschaltung von Stromquellen¶
Um in einem Stromkreis eine höhere Spannung oder eine größere nutzbare Stromstärke herbeizuführen, können auch mehrere Stromquellen (z.B. Batterien, Akkumulatoren oder Solarzellen) in Reihe oder parallel zueinander geschalten werden.
Reihenschaltung von Stromquellen
Werden 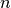 Stromquellen in Reihe geschaltet, so addieren sich ihre
einzelnen Spannungswerte
Stromquellen in Reihe geschaltet, so addieren sich ihre
einzelnen Spannungswerte 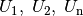 zu
einer Gesamtspannung
zu
einer Gesamtspannung 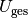 :
:
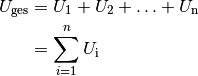
Diese Gleichung ist formal mit Gleichung (2) identisch. Der Unterschied liegt in der entgegengesetzten Wirkungsweise von Stromquellen und Widerständen:
- In einer Reihenschaltung wird durch das Hinzufügen eines zusätzlichen
Widerstands
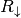 die an den übrigen Verbrauchern
anliegende Spannung auf
die an den übrigen Verbrauchern
anliegende Spannung auf 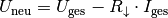 reduziert.
reduziert. - In einer Reihenschaltung wird durch das Hinzufügen einer zusätzlichen
Stromquelle
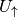 die an den übrigen Verbrauchern
anliegende Spannung auf
die an den übrigen Verbrauchern
anliegende Spannung auf 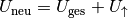 erhöht.
erhöht.
Schaltet man 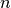 gleichartige Stromquellen in Reihe, so weist die
resultierende Stromquelle eine
gleichartige Stromquellen in Reihe, so weist die
resultierende Stromquelle eine 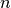 -fache Spannung auf.
-fache Spannung auf.
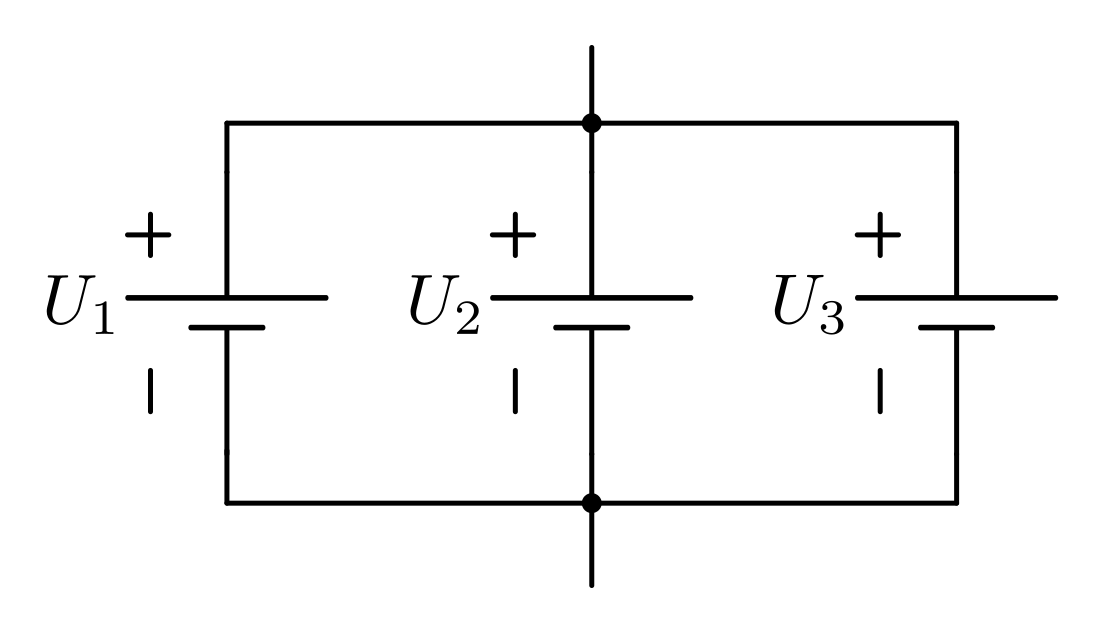
Parallelschaltung von Stromquellen
Werden 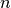 Stromquellen parallel zueinander geschaltet, so reduzieren sich
die Teilstromstärken
Stromquellen parallel zueinander geschaltet, so reduzieren sich
die Teilstromstärken 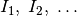 , die jede
einzelne Stromquelle zur gesamten Stromstärke
, die jede
einzelne Stromquelle zur gesamten Stromstärke 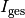 beisteuert.
beisteuert.
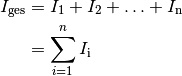
Diese Gleichung ist formal mit Gleichung (6) identisch. An dieser Stelle hat sie zweierlei gleichsam gültige Wirkungen zur Folge:
- Wird eine Stromquelle, die eine maximale Stromstärke
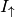 liefern kann, parallel zu einer bestehenden Stromquelle geschaltet, so erhöht
sich die insgesamt mögliche Stromstärke auf
liefern kann, parallel zu einer bestehenden Stromquelle geschaltet, so erhöht
sich die insgesamt mögliche Stromstärke auf 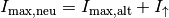 .[1]
.[1] - Wird eine weitere Stromquelle
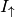 parallel zu einem
bestehenden Stromkreis geschaltet, so wird die bisherige Stromquelle auf
parallel zu einem
bestehenden Stromkreis geschaltet, so wird die bisherige Stromquelle auf
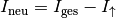 „entlastet“. Bei Stromquellen mit einem begrenzten Energiespeicher,
beispielsweise Batterien und Akkumulatoren, wird dadurch die Entladezeit
(„Lebensdauer“) entsprechend erhöht.[2]
„entlastet“. Bei Stromquellen mit einem begrenzten Energiespeicher,
beispielsweise Batterien und Akkumulatoren, wird dadurch die Entladezeit
(„Lebensdauer“) entsprechend erhöht.[2]
Bei einer Parallelschaltung von 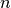 gleichartigen Stromquellen wird die
maximal mögliche Stromstärke um das
gleichartigen Stromquellen wird die
maximal mögliche Stromstärke um das 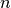 -fache erhöht beziehungsweise die
einzelnen von den Stromquellen bereitgestellten (Teil-)Stromstärken um das
-fache erhöht beziehungsweise die
einzelnen von den Stromquellen bereitgestellten (Teil-)Stromstärken um das
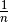 -fache reduziert.
-fache reduziert.
Reihen- und Parallelschaltung von Kondensatoren¶
Kondensatoren gehören ebenfalls zu den häufig verwendeten elektronischen
Bauteilen. Durch eine Reihen- oder Parallelschaltung mehrerer Kondensatoren
lässt sich ihre charakteristische Größe, die Kapazität 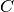 ,
beeinflussen.
,
beeinflussen.
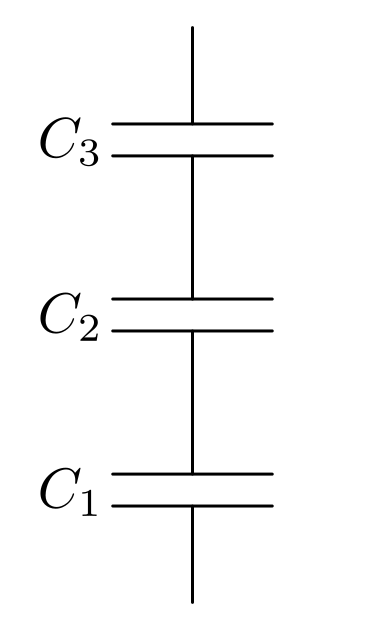
Reihenschaltung von Kondensatoren
Werden 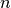 Kondensatoren in Reihe geschaltet, so werden bei Anlegen der
Spannung
Kondensatoren in Reihe geschaltet, so werden bei Anlegen der
Spannung 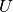 alle mit der gleichen Stromstärke
alle mit der gleichen Stromstärke 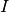 auf eine
Ladungsmenge
auf eine
Ladungsmenge 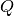 aufgeladen.
aufgeladen.
Wie bei Reihenschaltungen üblich, addieren sich dabei die an den einzelnen
Kondensatoren abfallenden Teilspannungen 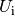 , die sich mit
Hilfe der allgemeinen Kondensator-Formel
, die sich mit
Hilfe der allgemeinen Kondensator-Formel 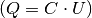 als
als
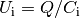 ausdrücken lassen:
ausdrücken lassen:
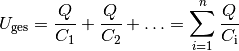
Um herauszufinden, wie mehrere Kondensatoren in ihrer Gesamtheit wirken, d.h.
welche Gesamt-Kapazität 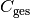 sich aus der Reihenschaltung
der
sich aus der Reihenschaltung
der 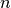 einzelnen Kondensatoren
einzelnen Kondensatoren 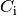 ergibt, muss man
beide Seiten der obigen Gleichung durch die konstante Ladung
ergibt, muss man
beide Seiten der obigen Gleichung durch die konstante Ladung 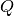 teilen.
Die linke Seite der Gleichung entspricht dann der Gesamtkapazität
teilen.
Die linke Seite der Gleichung entspricht dann der Gesamtkapazität
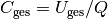 , die rechte Seite der Summe
aller Kehrwerte der einzelnen Kondensatoren:
, die rechte Seite der Summe
aller Kehrwerte der einzelnen Kondensatoren:
(7)¶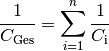
Wird zu einem bestehenden Kondensator ein weiterer in Reihe geschaltet, so nimmt die Gesamtkapazität ab. Kondensatoren verhalten sich in einer Reihenschaltung somit ähnlich wie Widerstände in einer Parallelschaltung.
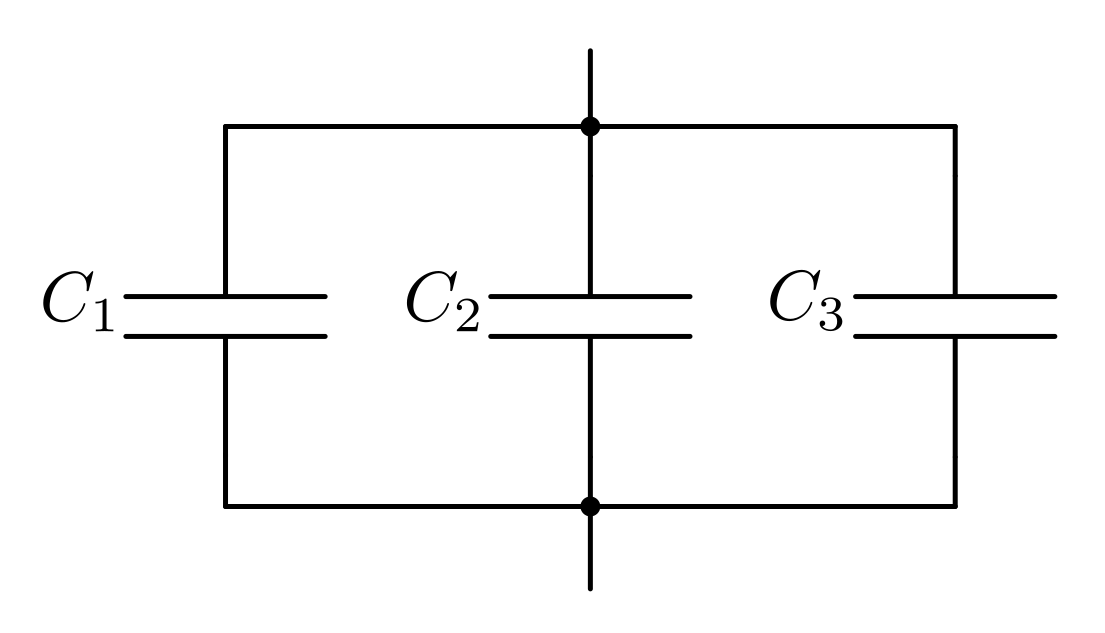
Parallelschaltung von Kondensatoren
Werden 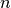 Kondensatoren parallel zueinander geschaltet, so liegt an
allen die gleiche Spannung
Kondensatoren parallel zueinander geschaltet, so liegt an
allen die gleiche Spannung 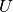 an. Der Gesamtstrom
an. Der Gesamtstrom 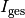 teilt sich in
teilt sich in 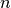 Teilströme auf, wodurch die einzelnen Kondensatoren mit
unterschiedlichen Ladungen
Teilströme auf, wodurch die einzelnen Kondensatoren mit
unterschiedlichen Ladungen 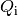 geladen werden.
geladen werden.
Mit Hilfe der allgemeinen Kondensator-Formel 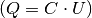 lässt sich
die Gesamt-Kapazität
lässt sich
die Gesamt-Kapazität 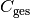 direkt ausdrücken:
direkt ausdrücken:
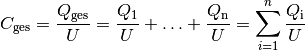
Die einzelnen Quotienten 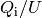 entsprechen dabei den einzelnen
Kapazitäten
entsprechen dabei den einzelnen
Kapazitäten 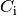 der parallel zueinander geschalteten
Kondensatoren. Somit gilt:
der parallel zueinander geschalteten
Kondensatoren. Somit gilt:
(8)¶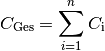
Eine Parallelschaltung zweier oder mehrerer Kondensatoren gleicht somit einem einzigen Kondensator mit einer entsprechend größeren Kapazität. Kondensatoren verhalten sich in einer Parallelschaltung somit ähnlich wie Widerstände in einer Reihenschaltung.
Stern-Dreieck-Umwandlung¶
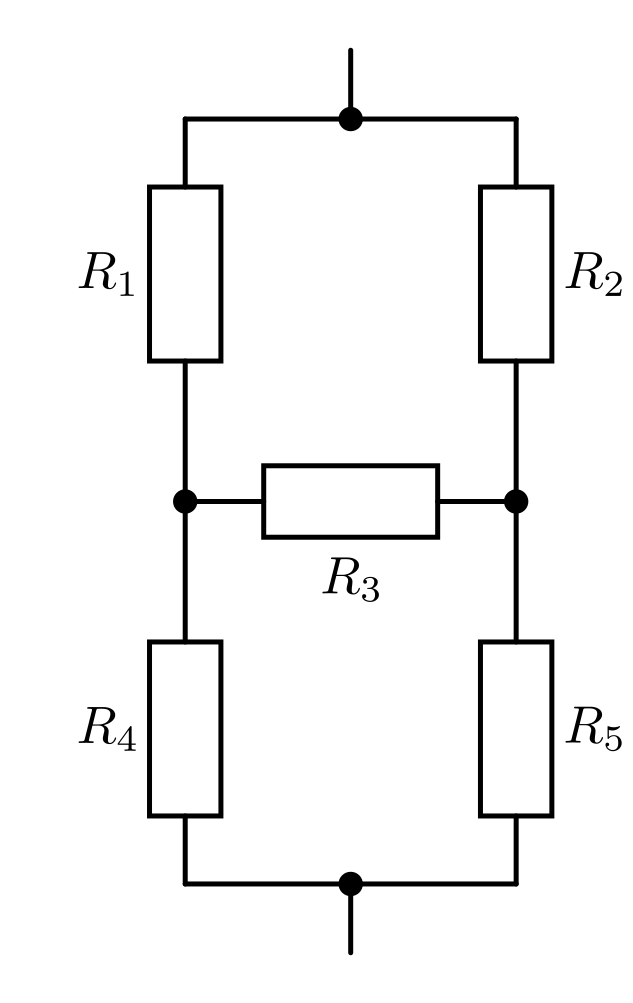
Um in einem Stromkreis mit mehreren Widerständen die einzelnen auftretenden Stromstärken und Spannungen zu bestimmen, können diese schrittweise durch Ersatz-Widerstände für Reihen- und Parallelschaltungen von Widerständen ersetzt werden. Bisweilen können allerdings auch Schaltungen auftreten, bei denen eine solche Ersetzung nicht unmittelbar möglich ist. Eine solche Schaltung ist in der folgenden Abbildung beispielhaft gezeigt:
Bei der obigen Beispiel-Schaltung kann man beispielsweise nicht unmittelbar
sagen, ob der Widerstand 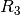 nun in Reihe oder parallel zu den übrigen
Widerständen geschaltet ist. In so einem Fall ist es jedoch möglich, eine
„dreieckige“ Schaltung in eine „sternförmige“ umzuwandeln:
nun in Reihe oder parallel zu den übrigen
Widerständen geschaltet ist. In so einem Fall ist es jedoch möglich, eine
„dreieckige“ Schaltung in eine „sternförmige“ umzuwandeln:
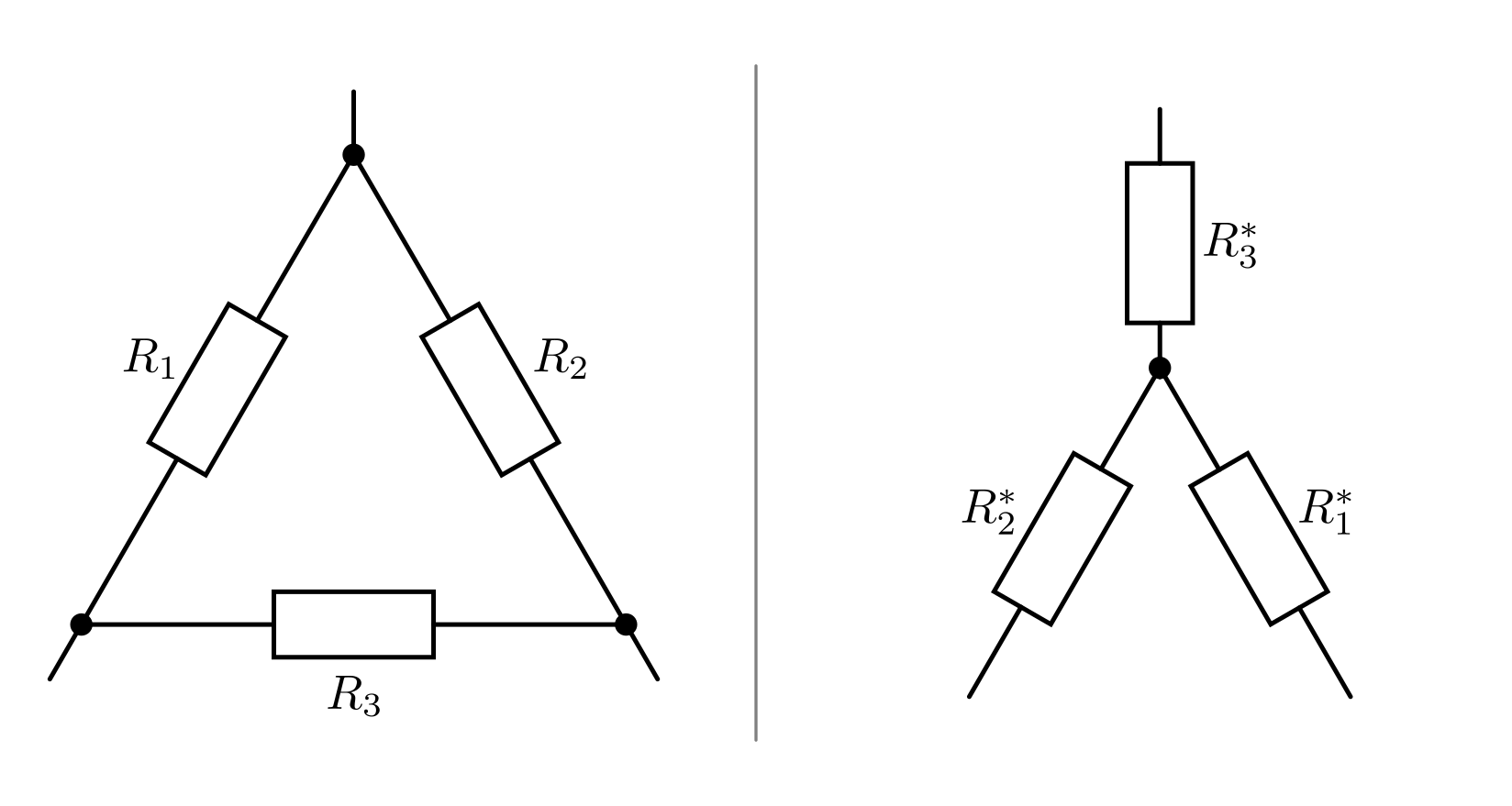
Bei einer derartigen „Dreieck-Stern-Umwandlung“ werden sowohl die Anordnungen
wie auch die Bezeichnungen der Widerstände geändert. Die Zuordnung geschieht
dabei wie bei einem geometrischen Rechteck, bei dem beispielsweise die
Dreieck-Seite  dem Punkt
dem Punkt 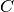 gegenüberliegt.
gegenüberliegt.
Die Werte der durch eine Dreieck-Stern-Umwandlung resultierenden Widerstände können folgendermaßen berechnet werden:
![R_1^{*} &= \frac{R_2 \cdot R_3}{R_1 + R_2 + R_3} \\[4pt]
R_2^{*} &= \frac{R_1 \cdot R_3}{R_1 + R_2 + R_3} \\[4pt]
R_3^{*} &= \frac{R_1 \cdot R_2}{R_1 + R_2 + R_3}](../_images/math/2bb53d5aa78c27b8845e321ee0989c334daae297.png)
Die resultierenden Widerstandswerte sind somit jeweils gleich dem Produkt der beiden anliegenden Widerstände, geteilt durch die Summe aller drei Widerstände.
Die Umwandlung kann bei Bedarf auch in der umgekehrten Richtung vorgenommen werden. Für die Werte der durch eine Stern-Dreieck-Umwandlung resultierenden Widerstände gilt entsprechend:
Beispiel:
In der am Anfang dieses Abschnitts abgebildeten Stern-Dreieck-Beispielschaltung soll für
![R_1 = R_2 = \unit[10]{\Omega}](../_images/math/bec07445572e0f0953fa08efad9931fef77bf3bc.png) ,
, ![R_3 =
\unit[20]{\Omega}](../_images/math/111fcdd3c28ebbcdf4b4eedb1470422ae2e847f3.png) und
und ![R_4 = R_5 = \unit[50]{\Omega}](../_images/math/a841281659797286b9448c7180483469ed478802.png) gelten. Wie groß
ist in diesem Fall der Gesamtwiderstand
gelten. Wie groß
ist in diesem Fall der Gesamtwiderstand 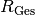 dieser
Schaltung?
dieser
Schaltung?Nimmt man für Anordnung der Widerstände
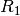 ,
, 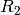 und
und
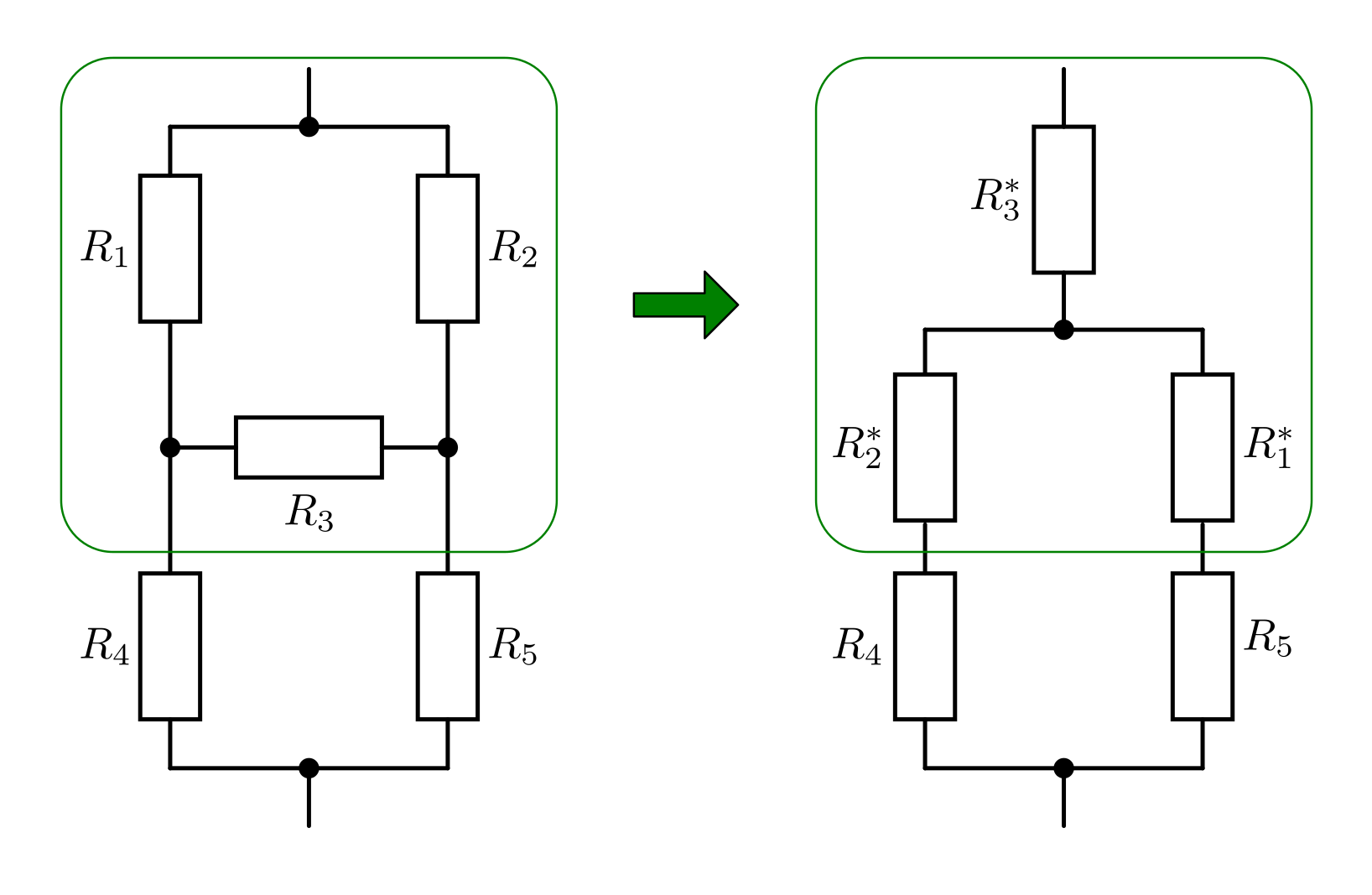
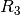 eine Dreieck-Stern-Umwandlung vor, so erhält man eine Schaltung,
die sich auf eine Reihen- und Parallelschaltung von Widerständen zurückführen
lässt. Für die „neuen“ Widerstandswerte
eine Dreieck-Stern-Umwandlung vor, so erhält man eine Schaltung,
die sich auf eine Reihen- und Parallelschaltung von Widerständen zurückführen
lässt. Für die „neuen“ Widerstandswerte 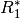 ,
, 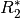 und
und
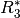 gilt dabei:
gilt dabei:![R_1^{*} &= \frac{R_2 \cdot R_3}{R_1 + R_2 + R_3} = \unit[\frac{10 \cdot
20}{10 + 10 + 20}]{\Omega} = \unit[5,0]{\Omega} \\[4pt] R_2^{*} &=
\frac{R_1 \cdot R_3}{R_1 + R_2 + R_3} = \unit[\frac{10 \cdot 20}{10 + 10 +
20}]{\Omega} = \unit[5,0]{\Omega} \\[4pt] R_3^{*} &= \frac{R_1 \cdot
R_2}{R_1 + R_2 + R_3} = \unit[\frac{10 \cdot 10}{10 + 10 + 20}]{\Omega} =
\unit[2,5]{\Omega}](../_images/math/6866900b91bbe27a2f2a8825600770173cf75f6f.png)
Nach der Umwandlung sind die Widerstände
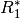 und
und 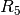 sowie
die Widerstände
sowie
die Widerstände 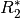 und
und 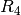 in Reihe geschalten. Da in
diesem Fall
in Reihe geschalten. Da in
diesem Fall 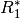 und
und 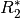 beide den Wert
beide den Wert
![\unit[5,0]{\Omega}](../_images/math/dbf11ccfdb61e649cfcc860650828d55132135fa.png) sowie
sowie 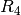 und
und 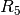 beide den Wert
beide den Wert
![\unit[50]{\Omega}](../_images/math/dbbdd04e545a0717df4d872fbaa7324b9d6575fd.png) haben, ergibt sich für die beiden Ersatzwiderstände
haben, ergibt sich für die beiden Ersatzwiderstände
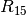 und
und 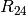 :
:![R_{\mathrm{15}} &= R_1^{*} + R_5 = \unit[5,0]{\Omega} + \unit[50]{\Omega} =
\unit[55]{\Omega} \\
R_{\mathrm{25}} &= R_2^{*} + R_5 = \unit[5,0]{\Omega} + \unit[50]{\Omega} =
\unit[55]{\Omega} \\](../_images/math/8b8c98f5d883d692f3832130e9aaffc0aa3bc407.png)
Die Ersatz-Widerstände
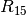 und
und 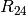 sind parallel zueinander geschaltet; für den zugehörigen Ersatz-Widerstand
sind parallel zueinander geschaltet; für den zugehörigen Ersatz-Widerstand
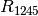 ergibt sich damit:
ergibt sich damit:![R_{\mathrm{1245}} = \frac{1}{\frac{1}{R_{24}} + \frac{1}{R_{35}} } =
\unit[\frac{1}{\frac{1}{55} + \frac{1}{55}}]{\Omega} = \unit[27,5]{\Omega}](../_images/math/acd0e2f7f56d96ec02b3853012cc5b0eca1b4391.png)
Dieser Ersatzwiderstand ist schließlich in Reihe mit
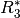 geschaltet; somit ergibt sich als Gesamt-Widerstand
geschaltet; somit ergibt sich als Gesamt-Widerstand ![R_{\mathrm{Ges}} =
R_3^{*} + R_{\mathrm{1245}} = \unit[(2,5+ 27,5)]{\Omega} =
\unit[30]{\Omega}](../_images/math/ef5276169ff75d411dbca94660f68701cc5a727e.png) .
.
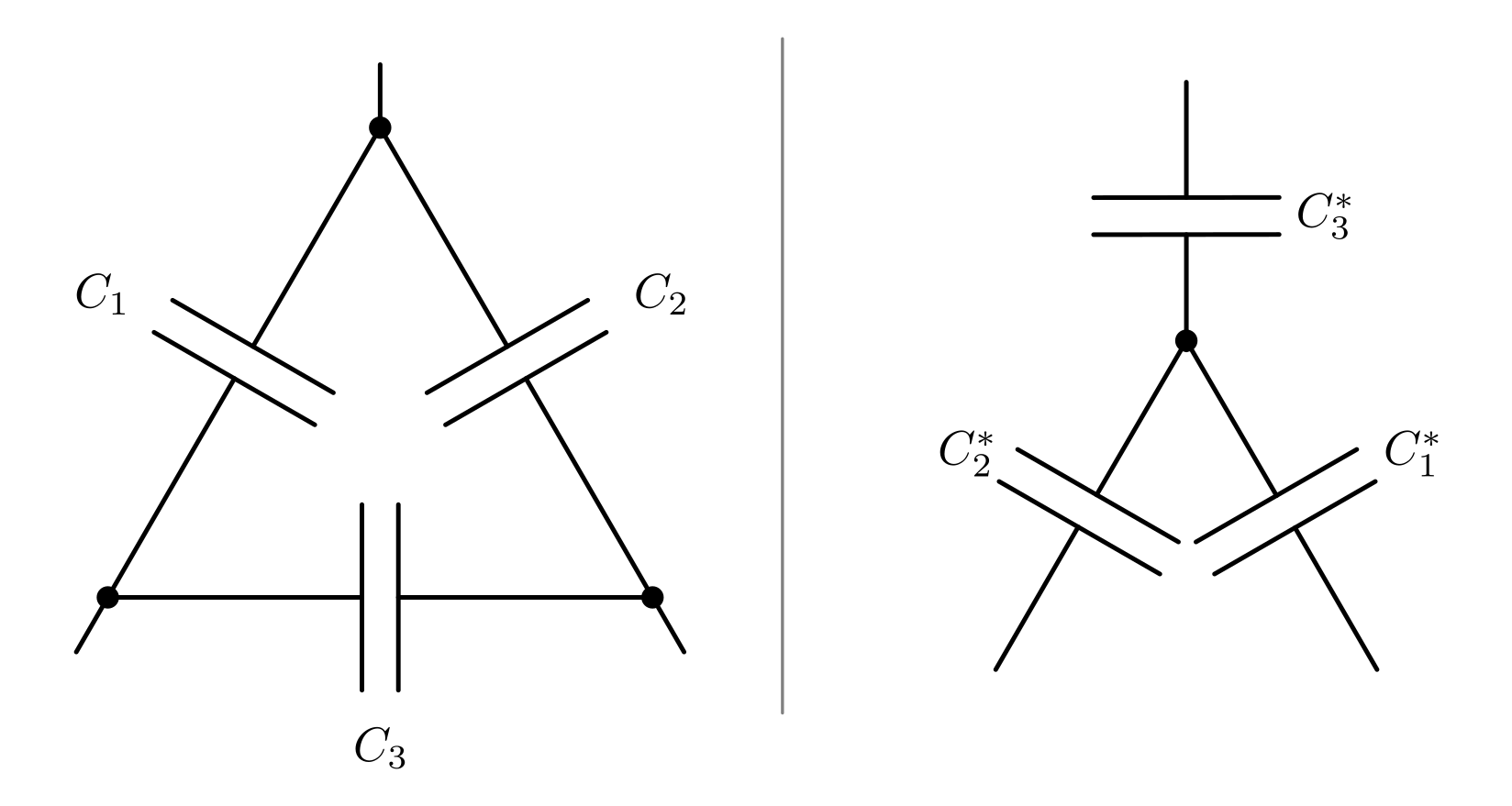
Stern-Dreieck-Umwandlung bei Kondensatoren
Kondensatoren verhalten sich bei Reihen- beziehungsweise Parallelschaltungen genau umgekehrt wie Widerstände: Bei Parallelschaltungen addieren sich ihre Kapazitätswerte, bei Reihenschaltungen hingegen die Kehrwerte ihrer Kapazitäten.
Man kann dennoch das Prinzip der Stern-Dreieck-Umwandlung auch auf Kondensatoren
übertragen, wenn man mit den Kehrwerten ihrer Kapazitäten beziehungsweise mit
den entsprechenden Blindwiderständen
rechnet 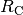 der einzelnen Kondensatoren rechnet.[3] Man
erhält dabei folgende Umrechnungen:
der einzelnen Kondensatoren rechnet.[3] Man
erhält dabei folgende Umrechnungen:
Bei einer Dreieck-Stern-Umwandlung von Kondensatoren können die resultierenden Werte der Kapazitäten folgendermaßen berechnet werden:
![C_1^{*} &= \frac{C_1 \cdot C_2 + C_1 \cdot C_3 + C_2 \cdot C_3}{C_1}
\\[4pt]
C_2^{*} &= \frac{C_1 \cdot C_2 + C_1 \cdot C_3 + C_2 \cdot C_3}{C_2}
\\[4pt]
C_3^{*} &= \frac{C_1 \cdot C_2 + C_1 \cdot C_3 + C_2 \cdot C_3}{C_3}](../_images/math/2b1c0720bd89a0e4572e6c07dd1df39106c06c7d.png)
Für die Werte der durch eine Stern-Dreieck-Umwandlung resultierenden Kapazitäten gilt entsprechend:
![C_1 &= \frac{C_2^{*} \cdot C_3^{*}}{C_1^{*} + C_2^{*} + C_3^{*}} \\[4pt]
C_2 &= \frac{C_1^{*} \cdot C_3^{*}}{C_1^{*} + C_2^{*} + C_3^{*}} \\[4pt]
C_3 &= \frac{C_1^{*} \cdot C_2^{*}}{C_1^{*} + C_2^{*} + C_3^{*}}](../_images/math/373b105b41b4dd374053b9cf1f9bb5b8d5a5fd60.png)
Auch bei Kondensatoren werden Stern-Dreieck- beziehungsweise Dreieck-Stern-Umwandlungen so lange durchgeführt, bis sich aus den resultierenden Ersatz-Kapazitäts-Werten eine Schaltung ergibt, die nur noch aus Reihen- und/oder Parallelschaltungen von Kondensatoren besteht.
Anmerkungen:
| [1] | Dies ist in der Praxis von Nutzen, wenn weitere (Verbraucher-)Widerstände
parallel zu einem bestehenden Stromkreis geschaltet werden: Die Spannung
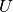 bleibt dabei unverändert, der Gesamt-Widerstand nimmt ab und die
nötige Stromstärke steigt. Um eine Batterie beziehungsweise einen
Akkumulator nicht zu überlasten, wird auch die bestehende Stromquelle um
eine oder mehrere (meist gleichartig gebaute) parallel geschaltene
Stromquellen erweitert. bleibt dabei unverändert, der Gesamt-Widerstand nimmt ab und die
nötige Stromstärke steigt. Um eine Batterie beziehungsweise einen
Akkumulator nicht zu überlasten, wird auch die bestehende Stromquelle um
eine oder mehrere (meist gleichartig gebaute) parallel geschaltene
Stromquellen erweitert. |
| [2] | Die gespeicherte Energiemenge einer Batterie oder eines Akkumulators ist
gleich 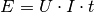 , wobei , wobei 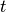 die Entladungszeit
angibt. Bei einer Parallelschaltung bleibt die Spannung die Entladungszeit
angibt. Bei einer Parallelschaltung bleibt die Spannung 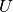 unverändert. Die gleiche Energiemenge
unverändert. Die gleiche Energiemenge 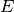 entlädt sich somit aufgrund
der niedrigeren Stromstärke entlädt sich somit aufgrund
der niedrigeren Stromstärke 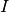 über einen entsprechend längeren
Zeitraum über einen entsprechend längeren
Zeitraum 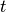 . . |
| [3] | Für den Blindwiderstand
Die Frequenz |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

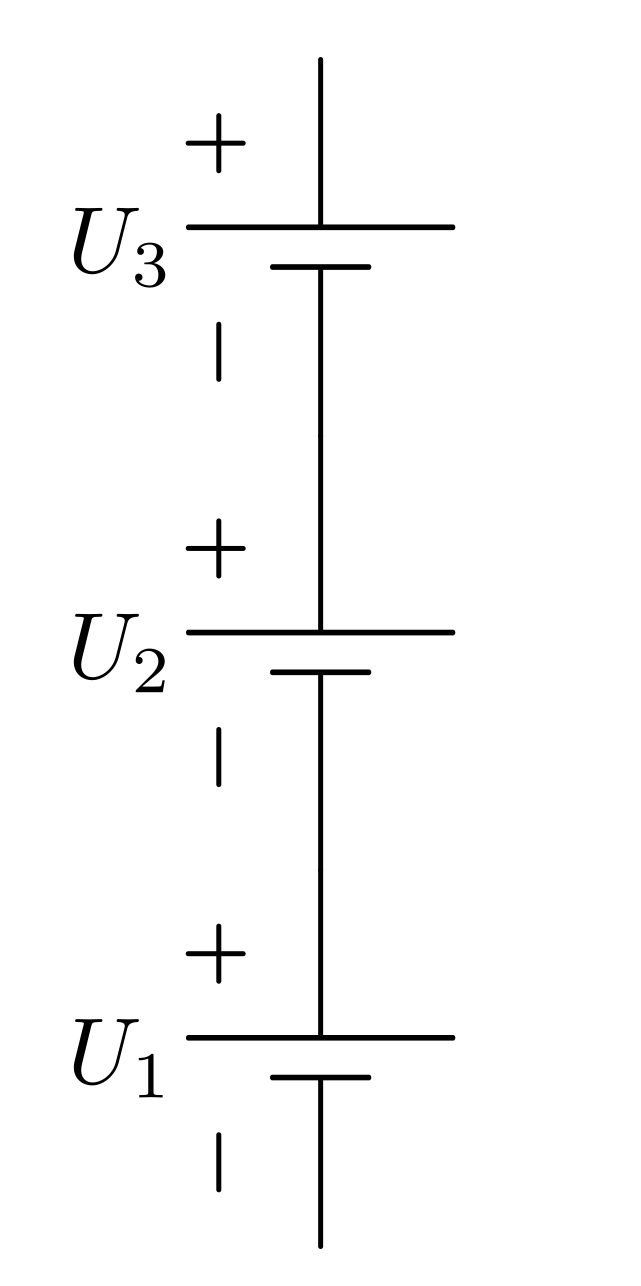
![R_1 &= R_2^{\,*} + R_3^{*} + \frac{R_2^{*} \cdot R_3^{*}}{R_1^{*}} \\[4pt]
R_2 &= R_1^{\,*} + R_3^{*} + \frac{R_1^{*} \cdot R_3^{*}}{R_2^{*}} \\[4pt]
R_3 &= R_1^{\,*} + R_2^{*} + \frac{R_1^{*} \cdot R_2^{*}}{R_3^{*}}](../_images/math/38e7004703b4df42401874a52b8cf453bd90ac12.png)
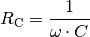
 des Wechselstroms ist bei einer
Stern-Dreieck-Umwandlung eine Konstante und kann bei der Umwandlung
„ausgeklammert“ werden.
des Wechselstroms ist bei einer
Stern-Dreieck-Umwandlung eine Konstante und kann bei der Umwandlung
„ausgeklammert“ werden.