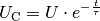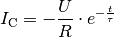Kondensatoren¶
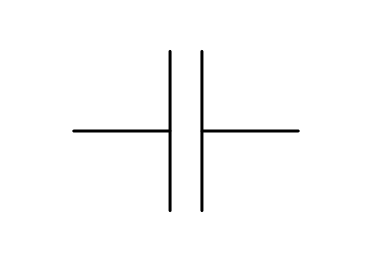
Ein Kondensator ist ein kleiner Ladungsspeicher. Er besteht im wesentlichen aus zwei Metallflächen, die sich im Bauteil – durch einen Isolator voneinander getrennt – gegenüber liegen. Kondensatoren stellen somit technische Verwirklichungen von Plattenkondensatoren dar.
Kondensatoren werden in elektrischen Schaltkreisen zu vielerlei Zwecken eingesetzt: Sie können beispielsweise elektrische Energie zwischenspeichern, Schwankungen in Gleichspannungs-Netzteilen ausgleichen, Frequenzen filtern oder das Verhalten von Kippschaltungen beeinflussen. Sie sind daher als elementares Bauteil in fast jeder Schaltung zu finden.
„Normale“ Kondensatoren¶
Ohne eine anliegende Spannung verteilen sich die Elektronen im Kondensator gleichmäßig über die Metallplatten und die Verbindungsleitungen. Liegt an einem Kondensator eine Gleichspannung an, so fließen kurzzeitig zusätzliche Elektronen auf die mit dem Minus-Pol verbundene Metallfläche, von der mit dem Plus-Pol verbundenen Metallfläche werden Elektronen weggezogen – die Kondensator-Platten laden sich elektrisch auf.
Während sich der Kondensator durch den externen Stromfluss auflädt, erhöht sich die Spannung, die zwischen seinen Metallplatten anliegt – der Kondensator wird selbst zu einer kleinen Spannungsquelle. Allerdings ist die Menge an elektrischer Ladung, die der Kondensator bei einer anliegenden externen Spannung speichern kann, begrenzt.
- Definition:
- Das Verhältnis aus maximal speicherbarer Ladung
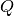 bei einer externen
Spannung
bei einer externen
Spannung 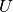 wird als Kapazität
wird als Kapazität 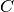 des Kondensators bezeichnet:
des Kondensators bezeichnet:
(1)¶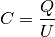
- Einheit:
- Die Kapazität eines Kondensators wird in Farad
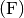 angegeben.
angegeben.
![\unit[1]{F} = \frac{\unit[1]{C}}{\unit[1]{V}}](../_images/math/a5e24ef25c2145ca4209f2561e8f6a0f0d43b866.png)
Beispiele:
- Ein Kondensator, der durch eine Stromstärke von einem Ampere in einer Sekunde auf eine Spannung von einem Volt aufgeladen wird, hat eine Kapazität von einem Farad. Eine derartige Kapazitätsmenge ist enorm hoch.
- Die Werte von normalen Folien- und Keramik-Kondensatoren liegen im Bereich
einiger
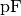 - oder
- oder 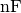 , maximal einiger
, maximal einiger
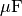 . Der Kapazitätswert ist auf jedem Kondensator mit
der unten genannten Notation aufgedruckt.
. Der Kapazitätswert ist auf jedem Kondensator mit
der unten genannten Notation aufgedruckt.
![\unit[1]{pF} &= \unit[10 ^{-12}]{F} =
\unit[\frac{1}{1\,000\,000\,000\,000}]{F} = \unit[0,000\,000\,000\,001]{F}
\\[4pt]
\unit[1]{nF} &= \unit[10 ^{-9}]{F} =
\unit[\frac{1}{1\,000\,000\,000}]{F} = \unit[0,000\,000\,001]{F} \\[4pt]
\unit[1]{\mu F} &= \unit[10 ^{-6}]{F} =
\unit[\frac{1}{1\,000\,000}]{F} = \unit[0,000\,001]{F}](../_images/math/5db3e8989abf2a6d8e77518783679db89bbb0370.png)
Notation von Kondensatorwerten
Auf jedem Kondensator ist aufgedruckt, welche Kapazität er besitzt und welche elektrische Spannung maximal an ihm anliegen darf. Die Werte werden – ähnlich wie Widerstandswerte – mit folgenden Besonderheiten angegeben:
Der Kapazitätswert eines Kondensators, beispielsweise
![\unit[10]{nF}](../_images/math/935bc283c44f0e4790caba95c645b6cb669425b0.png) ,
wird in Schaltplänen und auf Bauteilen oft in Klarschrift angegeben
(
,
wird in Schaltplänen und auf Bauteilen oft in Klarschrift angegeben
(![\unit[10]{n}](../_images/math/25f48849510f6683ed404ab58c985b57ee241b6f.png) , das „F“ wird weggelassen). Teilweise findet man den
Kapazitätswert eines Kondensators jedoch auch in Potenzschreibweise
(
, das „F“ wird weggelassen). Teilweise findet man den
Kapazitätswert eines Kondensators jedoch auch in Potenzschreibweise
(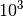 ) aufgedruckt. Hierbei geben die ersten beiden Ziffern den
Kondensator-Wert
) aufgedruckt. Hierbei geben die ersten beiden Ziffern den
Kondensator-Wert 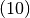 und die dritte Ziffer die Zehnerpotenz
und die dritte Ziffer die Zehnerpotenz 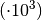 an. Die Wertangabe bezieht sich
dabei auf Pikofarad als kleinste Kapazität handelsüblicher Kondensatoren. Es
gilt:
an. Die Wertangabe bezieht sich
dabei auf Pikofarad als kleinste Kapazität handelsüblicher Kondensatoren. Es
gilt:![\unit[1]{nF} &= \unit[1\,000]{pF} = \unit[1 \cdot 10^3]{pF} \\[4pt]
\unit[1]{\mu F} &= \unit[1\,000]{nF} = \unit[1 \cdot 10^6]{pF}](../_images/math/fd0747b8ea3d32f1113214d6c190c96510968e30.png)
Ähnlich wie bei Widerständen werden Nachkommastellen stets hinter den Potenzfaktor geschrieben; eine Kapazitätsangabe von
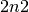 entspricht
somit einem Kapazitätswert von
entspricht
somit einem Kapazitätswert von ![\unit[2,2]{nF}](../_images/math/968140278d098ffef4d909be2de8219e483b2c50.png) . Auf diese Weise ist
ausgeschlossen, dass man eine Kommastelle aus Versehen „überlesen“ könnte.
. Auf diese Weise ist
ausgeschlossen, dass man eine Kommastelle aus Versehen „überlesen“ könnte.Nach der Kapazitätsangabe ist auf Kondensatoren meist direkt ein einzelner Buchstabe aufgedruckt, der die Toleranzklasse des Kondensators angibt.
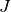 bedeutet beispielsweise eine Toleranz von
bedeutet beispielsweise eine Toleranz von 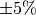 .
.Schließlich ist noch der Wert der maximalen Spannung aufgedruckt, die an den Kondensator angelegt werden darf (beispielsweise
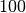 für
für
![\unit[100]{Volt}](../_images/math/2c4a1a7401046228108675b93de5dd27d9f42a3e.png) ).
).
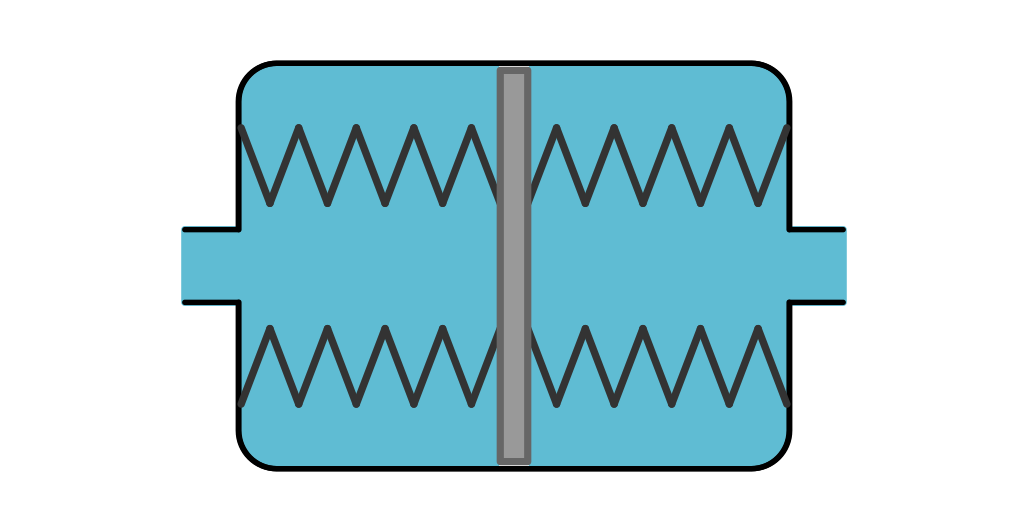
Anschauliches Modell für Kondensatoren
Ein einfaches physikalisches Modell zur Beschreibung von Stromstärke, Spannung und Widerstand ist es, sich einen elektrischen Stromfluss wie einen Wasserstrom vorzustellen. Bleibt man bei diesem Modell, so kann man sich für einen Kondensator etwa folgendes Modell vorstellen: Bilden die Leitungen ein Röhrensystem, so kann man sich einen Kondensator als Hohlzylinder vorstellen, in dem sich ein genau passender, aber frei beweglicher Kolben befindet; dieser soll also einerseits den Hohlzylinder in zwei voneinander getrennte Halbkammern unterteilen, andererseits jedoch ohne nennenswerte Reibung beweglich sein. Im Ruhezustand soll der Kolben durch zwei an den Seitenwänden befestigten Schraubenfedern in einer mittigen Position gehalten werden.
Wird in diesem Modell beispielsweise auf die linke Seite des Kolbens eine größerer Druck ausgeübt als auf die rechte, so verschiebt sich der Kolben nach rechts. Man erhält dabei scheinbar einen „Stromfluss“ durch den Kondensator, denn links fließt ebenso viel (Wasser) in ihn hinein wie auf der rechten Seite herausfließt. Es handelt sich zwar nicht um die selben Wasser-Teilchen, da die beiden Halb-Kammern voneinander isoliert sind, aber rein quantitativ kann man trotz des Kolbens als Trennschicht einen Transport an Wasserteilchen „durch“ den Kondensator beobachten.
Wird der Kolben durch das zufließende Wasser aus seiner Ruhelag ausgelenkt, so baut sich in den Schraubenfedern zunehmend eine (mechanische) Gegen-Spannung auf. Der Kolben wird solange verschoben, bis die Gegenspannung in den Federn den an einer Seite anliegenden Überdruck ausgleicht. Liegt kein einseitiger Überdruck mehr an, kehrt der Kolben in den Ruhezustand zurück, wodurch es wiederum zum Ladungstransport „durch“ den Kondensator kommt.
Kondensatoren im Gleichstromkreis
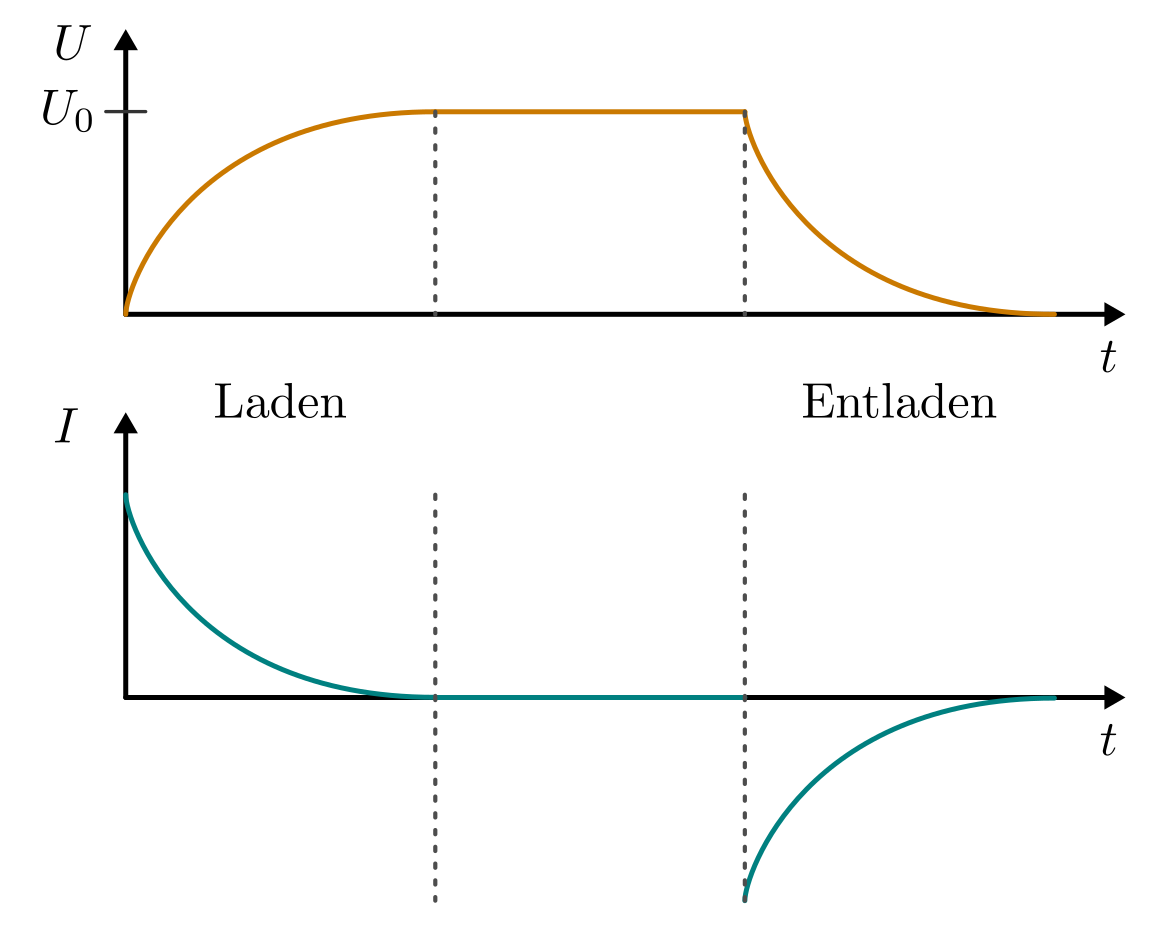
Um einen Kondensator komplett aufzuladen, sind je nach Kapazität des Kondensators und der Stärke des Ladestroms oft nur wenige Sekunden oder sogar Sekundenbruchteile nötig. Durch das Aufladen des Kondensators und die sich dabei aufbauende Spannung zwischen den Kondensatorplatten verläuft der Aufladevorgang anfangs schnell und dann zunehmend langsamer.
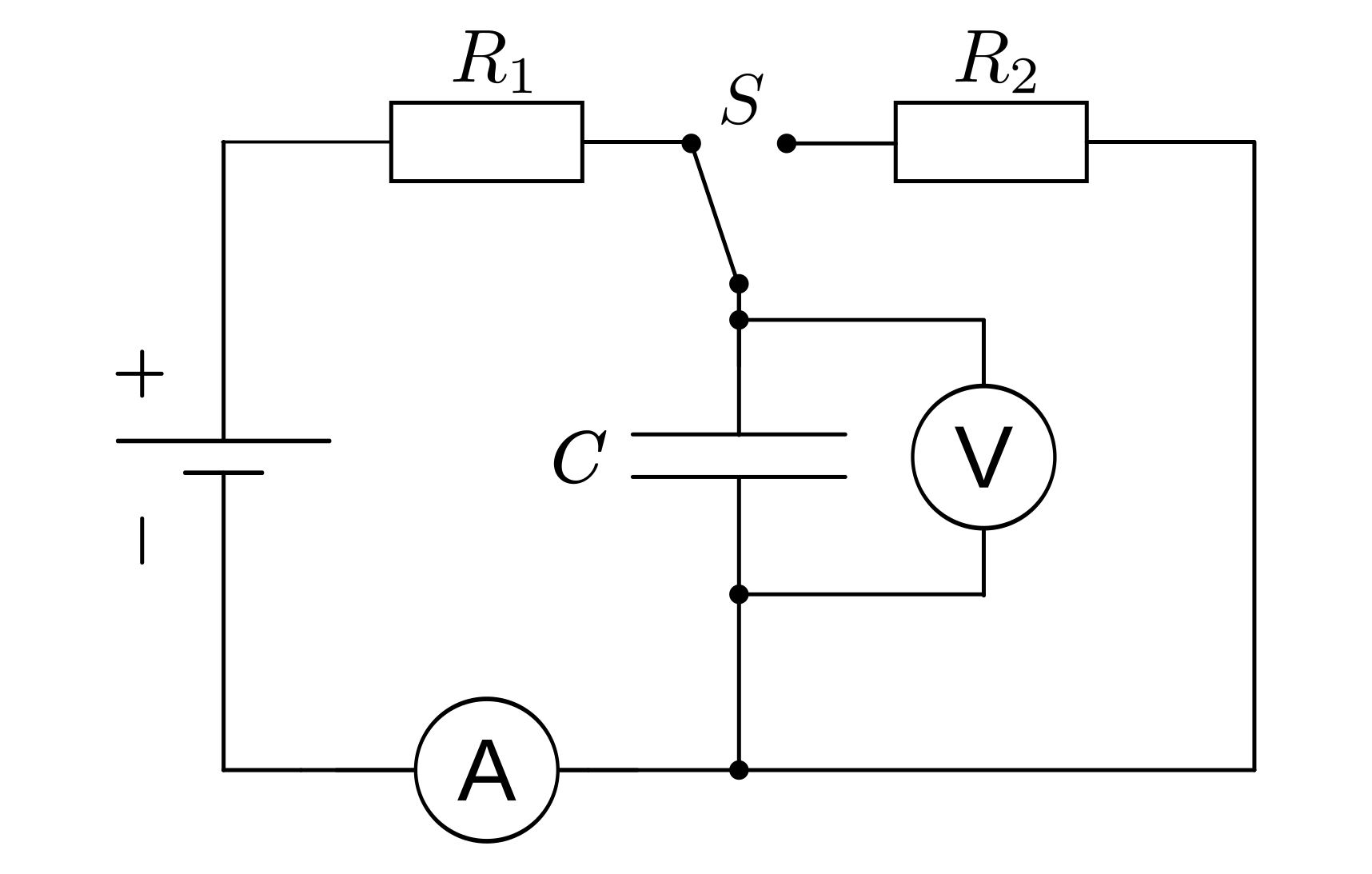
Prinzipieller Aufbau einer Schaltung zur Bestimmung der Ladekurve eines Kondensators mit Vorwiderstand.
Der Ladevorgang kommt dann zum Stillstand, wenn die Spannung
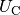 zwischen den beiden Kondensator-Platten gleich der
Ladespannung
zwischen den beiden Kondensator-Platten gleich der
Ladespannung 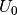 ist; der Kondensator ist dann geladen, und es kann kein
weiterer Strom mehr „durch“ den Kondensator fließen. Als Diagramm erhält man für
den Lade- beziehungsweise Entladevorgang eines Kondesators etwa folgende
Kennlinie:
ist; der Kondensator ist dann geladen, und es kann kein
weiterer Strom mehr „durch“ den Kondensator fließen. Als Diagramm erhält man für
den Lade- beziehungsweise Entladevorgang eines Kondesators etwa folgende
Kennlinie:
Aus mathematischer Sicht kann der zeitliche Verlauf der Spannung
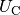 zwischen den Kondensator-Platten folgendermaßen
beschrieben werden:
zwischen den Kondensator-Platten folgendermaßen
beschrieben werden:
(2)¶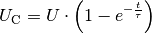
Für den Ladestrom 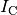 gilt entsprechend:
gilt entsprechend:
(3)¶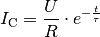
Hierbei ist 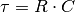 die sogenannte Zeitkonstante. Nach einer
Zeit von
die sogenannte Zeitkonstante. Nach einer
Zeit von 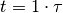 hat die Kondensator-Spannung
hat die Kondensator-Spannung
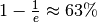 ihres Endwerts erreicht; der Ladestrom fällt
nach der gleichen Zeit auf auf
ihres Endwerts erreicht; der Ladestrom fällt
nach der gleichen Zeit auf auf 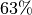 seines Anfangswertes ab.[1]
seines Anfangswertes ab.[1]
Kondensatoren im Wechselstromkreis
Legt man an einen Kondensator eine Wechselspannung an, so fließt wechselnd ein Lade- beziehungsweise Entladestrom. Ein Kondensator wirkt in einem Wechselstromkreis wie ein Widerstand.
Während der Auflade-Vorgänge wird elektrische Energie auf den Kondensator übertragen, die während der Entlade-Vorgänge wieder vom Kondensator abgegeben wird; im zeitlichen Durchschnitt ist daher der Mittelwert der auftretenden elektrischen Leistungen an einem (idealen) Kondensator gleich Null. Man spricht in diesem Zusammenhang auch von „Blindleistung“; den Kondensator bezeichnet man in einem Wechselstromkreis als „Blindwiderstand“ oder „kapazitativen Scheinwiderstand“.
Der kapazitative Scheinwiderstand ist von der Kapazität des
Kondensators und der Frequenz des Wechselstroms abhängig; je größer die
Kapazität 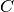 und je höher die Frequenz
und je höher die Frequenz 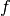 des Wechselstroms ist,
desto, desto niedriger ist der kapazitative Scheinwiderstand des Kondensators:
des Wechselstroms ist,
desto, desto niedriger ist der kapazitative Scheinwiderstand des Kondensators:
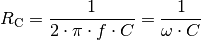
Hierbei wird mit 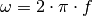 die Kreisfrequenz des
Wechselstroms bezeichnet.
die Kreisfrequenz des
Wechselstroms bezeichnet.
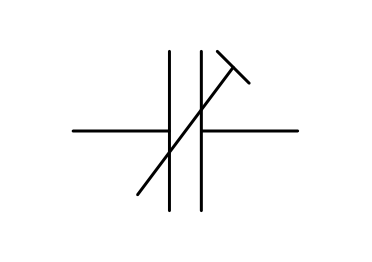
Trimmkondensatoren¶
Als Trimmkondensator (auch Dreh-Kondensator oder kurz „Drehko“ genannt) bezeichnet man einen Kondensator mit einer einstellbaren Kapazität; diese reicht von Null bis zum angegebenen Höchstwert.
Der Kapazitätswert von Drehkondensatoren kann üblicherweise mittels eines
Drehknopfs eingestellt werden. Da sich bei den meisten Drehkondensatoren Luft
zwischen den Kondensatorplatten befindet, liegen die maximalen Kapazitätswerte
meist unter ![\unit[500]{pF}](../_images/math/ed6a224ef93255980d6ad03baa0c244000e05c38.png) . Derartige Kondensatoren werden
beispielsweise in Radios eingesetzt, um den Empfänger auf verschiedene
Senderfrequenzen einstellen zu können.
. Derartige Kondensatoren werden
beispielsweise in Radios eingesetzt, um den Empfänger auf verschiedene
Senderfrequenzen einstellen zu können.
Elektrolyt-Kondensatoren¶
Elektrolyt-Kondensatoren („Elkos“) haben meist hohe Kapazitätwerte von etwa
![\unit[0,1]{\mu F}](../_images/math/c86172624eeb4412491b9bb1d34caa9df09af45a.png) bis
bis ![\unit[1000]{\mu F}](../_images/math/e9b8ee1d0c1618f8d38057ca27fde9a3d3fa2c45.png) , oder sogar mehr.
Elektrolyt-Kondensatoren sind allerdings polarisiert, sie besitzen also jeweils
einen Plus- und einen Minus-Anschluss, die man nicht vertauschen darf. Die
Anschlüsse sind deutlich gekennzeichnet, meist durch aufgedruckte Minus-Zeichen
am Minus-Anschluss. Bei neuen Elkos kann man den Pluspol zusätzlich am längeren
Anschlussdraht erkennen.
, oder sogar mehr.
Elektrolyt-Kondensatoren sind allerdings polarisiert, sie besitzen also jeweils
einen Plus- und einen Minus-Anschluss, die man nicht vertauschen darf. Die
Anschlüsse sind deutlich gekennzeichnet, meist durch aufgedruckte Minus-Zeichen
am Minus-Anschluss. Bei neuen Elkos kann man den Pluspol zusätzlich am längeren
Anschlussdraht erkennen.
Bei der Verwendung von Elektrolyt-Kondensatoren muss man nicht nur auf richtige Polung achten, sondern auch berücksichtigen, dass ihre Kapazität im Laufe der Zeit beachtlich abnehmen kann. Elektrolyt-Kondensatoren sollten folglich nur an Stellen verbaut werden, an denen eine Abweichung des Kapazitätswerts für die Schaltung keine allzu große Rolle spielt.
Anmerkungen:
| [1] | Wird der Kondensator von der Spannungsquelle getrennt und über einen
Widerstand (4)¶ Für den Entladestrom (5)¶ |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

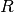 entladen, so gilt folgende Gleichung für die Spannung
entladen, so gilt folgende Gleichung für die Spannung