Grundschaltungen¶
Die folgenden Schaltungen dienen dem Kennenlernen der einzelnen Bauteile und
ihrer Grundfunktionen. Die Schaltungen im folgenden Abschnitt sind stets auf
eine ![\unit[9]{V}](../_images/math/d72464e9d3f0af08777997e0da6e5a1148bb200d.png) - Gleichspannung ausgelegt. Eine solche Spannung kann
beispielsweise mittels eines regelbaren Labornetzteils, einer Blockbatterie,
oder näherungsweise auch durch einen wiederaufladbaren und daher
umweltfreundlicheren Block-Akku bereitgestellt werden.
- Gleichspannung ausgelegt. Eine solche Spannung kann
beispielsweise mittels eines regelbaren Labornetzteils, einer Blockbatterie,
oder näherungsweise auch durch einen wiederaufladbaren und daher
umweltfreundlicheren Block-Akku bereitgestellt werden.
Spannungsteiler¶
Als Spannungsteiler bezeichnet man Schaltungen aus zwei oder mehr Widerständen, mit dem Ziel, eine anliegende Spannung gezielt in bestimmte Verhältnisse aufzuteilen.
Unbelastete Spannungsteiler¶
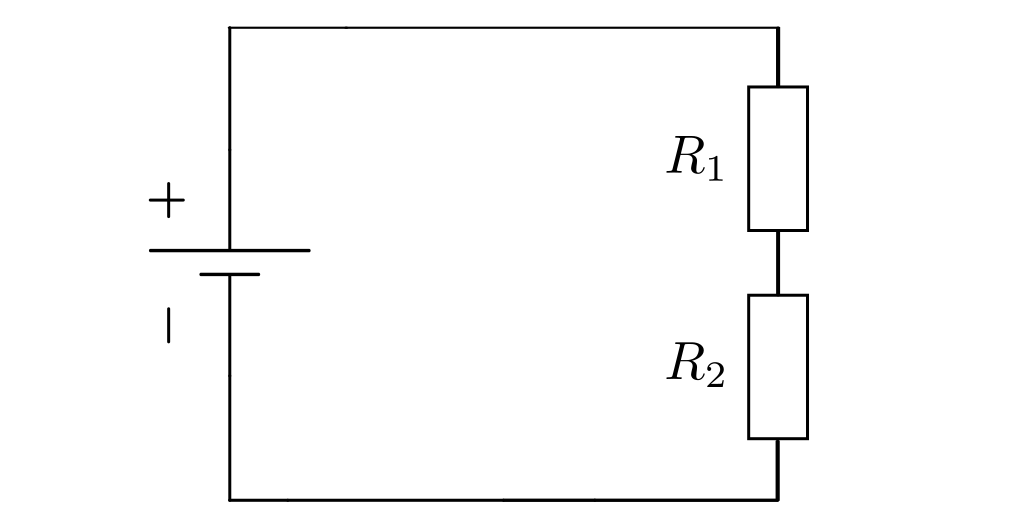
Eine sehr einfache, aber dennoch wichtige Grundschaltung besteht aus einer Reihenschaltung zweier Widerstände:
Eine solche Anordnung wird als „unbelasteter Spannungsteiler“ bezeichnet. Da es
sich um eine Reihenschaltung handelt, ist die Stromstärke 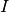 innerhalb
der Schaltung an allen Stellen gleich, während die Teilspannungen
innerhalb
der Schaltung an allen Stellen gleich, während die Teilspannungen 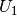 und
und 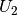 an den Widerständen
an den Widerständen 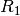 und
und 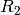 in Summe gleich
der anliegenden Gesamtspannung
in Summe gleich
der anliegenden Gesamtspannung 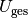 sind:
sind:
![I_{\mathrm{ges}} = I_1 = I_2 \\[6pt]
U_{\mathrm{ges}} = U_1 + U_2](../_images/math/dfddac9e86802028bd2fd57a6f63fbbac8569470.png)
Aus den beiden obigen Formeln sowie dem Ohmschen Gesetz 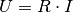 kann beispielsweise eine Formel zur Berechnung von
kann beispielsweise eine Formel zur Berechnung von
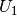 in Abhängigkeit von der Gesamtspannung
in Abhängigkeit von der Gesamtspannung 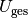 und
den beiden Widerständen
und
den beiden Widerständen 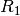 und
und 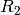 angegeben werden. Setzt man
in die zweite Gleichung
angegeben werden. Setzt man
in die zweite Gleichung 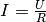 ein, so erhält man:
ein, so erhält man:
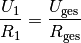
Diese Gleichung kann unmittelbar nach 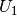 aufgelöst werden. Setzt man
für zudem
aufgelöst werden. Setzt man
für zudem 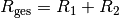 ein (Reihenschaltung!), so erhält
man schließlich:
ein (Reihenschaltung!), so erhält
man schließlich:
(1)¶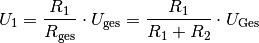
Am ersten Widerstand fällt somit der Anteil 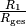 der Gesamtspannung ab. In gleicher Weise kann gezeigt werden, dass am zweiten
Widerstand die Spannung
der Gesamtspannung ab. In gleicher Weise kann gezeigt werden, dass am zweiten
Widerstand die Spannung 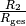 abfällt:
abfällt:
(2)¶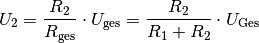
Die zwei Spannungen 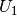 und
und 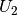 an den beiden Widerständen
stehen also zueinander im gleichen Werte-Verhältnis wie die Widerstände selbst.
an den beiden Widerständen
stehen also zueinander im gleichen Werte-Verhältnis wie die Widerstände selbst.
Beispiel:
Ein Stromkreis, der als Spannungsquelle eine
![\unit[9]{V}](../_images/math/d72464e9d3f0af08777997e0da6e5a1148bb200d.png) -Batterie hat,
besteht aus den zwei Widerständen
-Batterie hat,
besteht aus den zwei Widerständen ![R_1 = \unit[10]{\Omega}](../_images/math/41d726883444e0495fad57d8232cee58e5a05c18.png) und
und
![R_2 = \unit[90]{\Omega}](../_images/math/aa0e11d72bc90d5dd9e687e63cbe3000f7026d5d.png) . Wie groß sind die Spannungen
. Wie groß sind die Spannungen 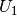 und
und
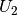 , die an
, die an 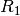 beziehungsweise
beziehungsweise 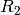 anliegen?
anliegen?Der Gesamtwiderstand der Schaltung beträgt
![R_{\mathrm{ges}} = R_1 + R_2
= \unit[100]{\Omega}](../_images/math/ce4c4222022469d141cdb55bee81d73ccf8c78c9.png) . Am den Widerständen liegen damit folgende Spannungen an:
. Am den Widerständen liegen damit folgende Spannungen an:![U_1 &= \frac{R_1}{R_{\mathrm{ges}}} \cdot U_{\mathrm{ges}}=
\frac{\unit[10]{\Omega}}{\unit[100]{\Omega}} \cdot \unit[9]{V} =
\unit[0,9]{V} \\[4pt]
U_2 &= \frac{R_2}{R_{\mathrm{ges}}} \cdot U_{\mathrm{ges}}=
\frac{\unit[90]{\Omega}}{\unit[100]{\Omega}} \cdot \unit[9]{V} =
\unit[8,1]{V}](../_images/math/31812fd1553516275e9559d92439c4f71528c748.png)
Das gleiche Spannungsverhältnis stellt sich ein, wenn man als Widerstandswerte beispielsweise
![R_1=\unit[100]{\Omega}](../_images/math/c898a7ae10155066e1652d79d8ec4dfc7a8f5b70.png) und
und ![R_2 =
\unit[900]{\Omega}](../_images/math/0b086402019a1af607c75bde1657a9635885d25a.png) wählt; in diesem Fall ist lediglich die Stromstärke in der
Schaltung um ein
wählt; in diesem Fall ist lediglich die Stromstärke in der
Schaltung um ein 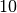 -faches geringer. Die Spannungen hängen hingegen
nicht von den konkreten Werten der Widerständen, sondern nur von ihrem
Größenverhältnis ab.
-faches geringer. Die Spannungen hängen hingegen
nicht von den konkreten Werten der Widerständen, sondern nur von ihrem
Größenverhältnis ab.
Belastete Spannungsteiler¶
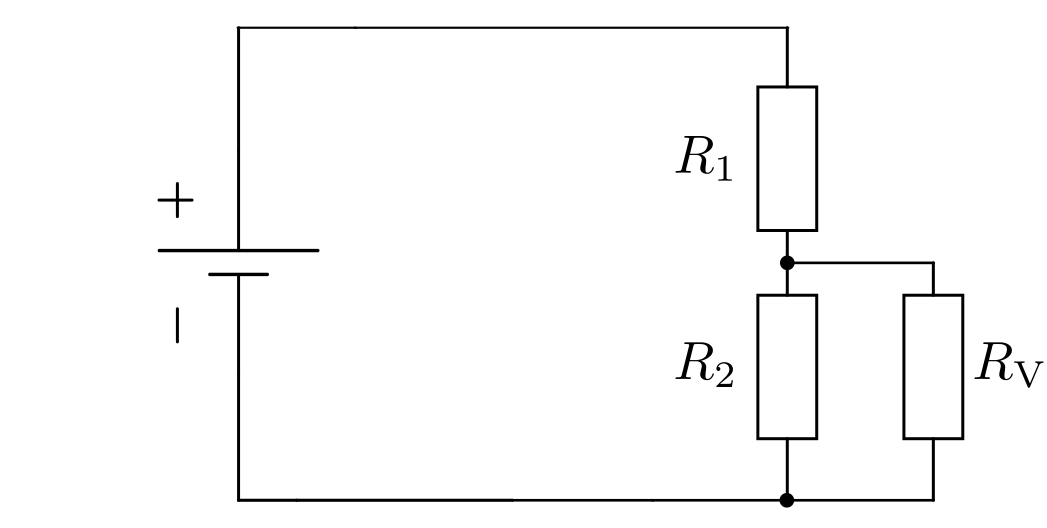
Bei einer Parallelschaltung zweier Widerstände ist die an beiden Widerständen anliegende Spannung gleich; zudem
hat sich im letzten Abschnitt gezeigt, dass man mittels eines Spannungsteilers
die anliegende Gesamtspannung in beliebig große Teilspannungen aufteilen kann.
Könnte man also nicht durch ein Parallelschalten eines Spannungsteilers zu einem
Verbraucher-Widerstand 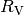 auch dort eine gewünschte
(geringere) Teilspannung erhalten?
auch dort eine gewünschte
(geringere) Teilspannung erhalten?
Die Antwort ist ein klares „Jain“, da sich beispielsweise durch das
Parallelschalten von 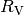 zum Widerstand
zum Widerstand 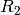 des
Spannungsteilers ein neuer Widerstandswert
des
Spannungsteilers ein neuer Widerstandswert 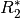 ergibt.
Für die Parallelschaltung dieser zwei Widerstände gilt nämlich:[1]
ergibt.
Für die Parallelschaltung dieser zwei Widerstände gilt nämlich:[1]
(3)¶
- Ist
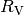 gegenüber
gegenüber 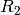 vergleichsweise groß, so ist
der Wert von
vergleichsweise groß, so ist
der Wert von 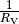 vergleichsweise gering, und es
ergibt sich
vergleichsweise gering, und es
ergibt sich 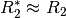 . Die am Verbraucher
anliegende Spannung entspricht in diesem Fall also in guter Näherung der am
Widerstand
. Die am Verbraucher
anliegende Spannung entspricht in diesem Fall also in guter Näherung der am
Widerstand 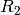 des unbelasteten Spannungsteilers anliegenden Spannung
des unbelasteten Spannungsteilers anliegenden Spannung
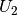 .
. - Je geringer der Wert von
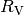 im Vergleich zum Wert von
im Vergleich zum Wert von
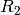 wird, desto geringer wird auch der Wert von
wird, desto geringer wird auch der Wert von 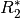 . Die
nun am Widerstand
. Die
nun am Widerstand 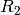 des belasteten Spannungsteilers anliegende
Spannung
des belasteten Spannungsteilers anliegende
Spannung 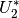 und damit auch die am Verbraucher anliegende Spannung
sinkt folglich gegenüber der Spannung
und damit auch die am Verbraucher anliegende Spannung
sinkt folglich gegenüber der Spannung 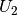 beim unbelasteten
Spannungsteiler ab.
beim unbelasteten
Spannungsteiler ab.
Für die Spannung 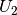 am belasteten Spannungsteiler gilt also:
am belasteten Spannungsteiler gilt also:
(4)¶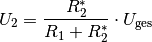
Um einer starken Änderung von 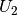 entgegenzuwirken, muss man bei einen
einen niederohmigen Spannungsteiler einsetzen; damit erhöht sich allerdings auch
der ungenutzte „Querstrom“ durch den Widerstand
entgegenzuwirken, muss man bei einen
einen niederohmigen Spannungsteiler einsetzen; damit erhöht sich allerdings auch
der ungenutzte „Querstrom“ durch den Widerstand 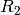 .
.
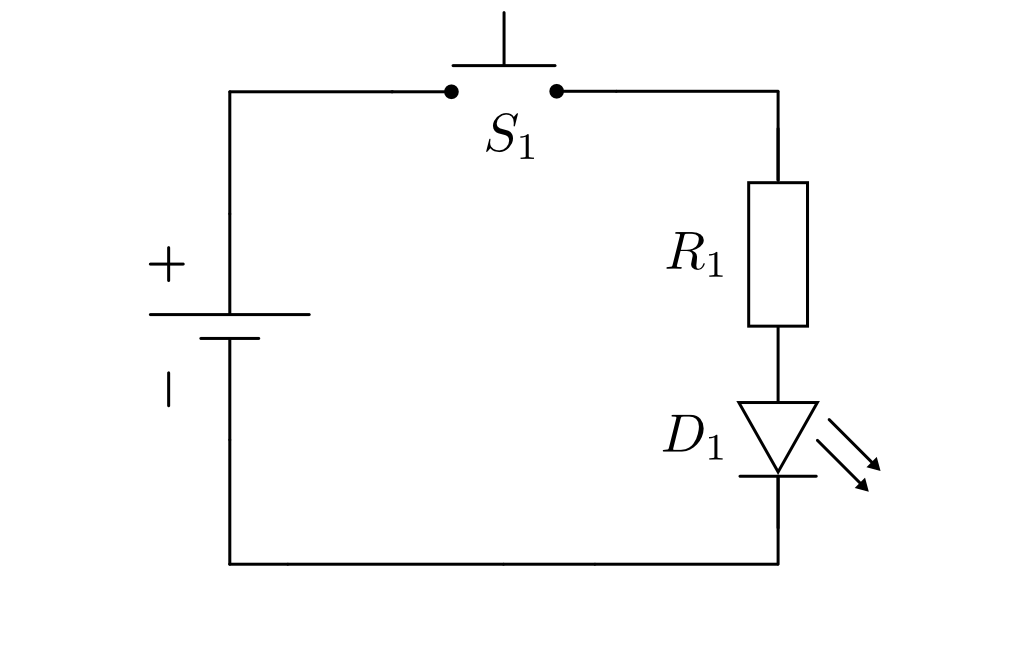
Leuchtdiode mit Vorwiderstand¶
Leuchtdioden („LEDs“) werden beim Experimentieren gerne
eingesetzt, um auf den ersten Blick zu erkennen, ob an einer bestimmten Stelle
Strom fließt oder nicht. Damit beispielsweise eine rote Leuchtdiode mit
„normaler“ Helligkeit aufleuchtet, benötigt sie eine Gleichspannung von etwa
![U = \unit[1,9]{V}](../_images/math/e420c01a0abb8c94b574b634a3668e0d954cedbf.png) .
.
Da zu hohe Spannungen (![U > \unit[2,5]{V}](../_images/math/57b5ffbf302c7abc7b201f2ff522c667514766ef.png) ) das Bauteil zum Überhitzen
bringen können, schaltet man vor eine Leuchtdiode
) das Bauteil zum Überhitzen
bringen können, schaltet man vor eine Leuchtdiode 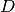 bei Bedarf stets
einen so genannten Vorwiderstand
bei Bedarf stets
einen so genannten Vorwiderstand 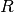 in Reihe. Damit hat man letztlich
einen Spannungsteiler mit einem Widerstand und einer Diode gebaut, was zur Folge
hat, dass an der LED nur noch ein Teil der Gesamt-Spannung anliegt.
in Reihe. Damit hat man letztlich
einen Spannungsteiler mit einem Widerstand und einer Diode gebaut, was zur Folge
hat, dass an der LED nur noch ein Teil der Gesamt-Spannung anliegt.
Bei einer Versorgungsspannung von ![U = \unit[9]{V}](../_images/math/3ee4ddce6280e2707c96845d95a394815f2bbcfc.png) muss am Vorwiderstand
eine Spannung von
muss am Vorwiderstand
eine Spannung von ![U_{\mathrm{R}} = \unit[7,1]{V}](../_images/math/b90808a0914948750b77f914c226075da6014124.png) abfallen, um eine
typische Betriebsspannung von
abfallen, um eine
typische Betriebsspannung von ![U_{\mathrm{LED}} = \unit[1,9]{V}](../_images/math/b209716e77acd20210181fdd3ff520b3f8aa0bb2.png) an der
Leuchtdiode zu erreichen. Beträgt der Wert des Vorwiderstandes beispielsweise
an der
Leuchtdiode zu erreichen. Beträgt der Wert des Vorwiderstandes beispielsweise
![R = \unit[470]{\Omega }](../_images/math/2956102bc0a2922b1929b29fb4995c9a72c4afad.png) , so ergibt sich nach dem Ohmschen Gesetz für die Schaltung folgende Stromstärke:
, so ergibt sich nach dem Ohmschen Gesetz für die Schaltung folgende Stromstärke:
![I = \frac{U_{\mathrm{R}}}{R} = \frac{\unit[7,1]{V}}{\unit[470]{\Omega }}
\approx \unit[0,015]{A} = \unit[15]{mA}](../_images/math/bd940d4f5d9014ecd4a2d7a7e1a4459cb906dfb7.png)
Diese Stromstärke fließt, da der Vorwiderstand und die Leuchtdiode als
Reihenschaltung vorliegen, auch durch die LED. Normale LEDs werden üblicherweise
mit Stromstärken von knapp ![\unit[20]{mA}](../_images/math/363d7fee9882e8356537c82e4e6944546447668c.png) betrieben, so dass ein
betrieben, so dass ein
![\unit[470]{\Omega}](../_images/math/99a5dca672a5de7c9c802b4175dc8eddf793edf4.png) -Widerstand bei einer anliegenden Spannung von
-Widerstand bei einer anliegenden Spannung von
![\unit[9]{V}](../_images/math/d72464e9d3f0af08777997e0da6e5a1148bb200d.png) keine schlechte Wahl ist.
keine schlechte Wahl ist.
Beispiel:
Wie groß müsste der Vorwiderstand einer LED allerdings exakt sein, wenn an dort bei einer anliegenden Spannung von
![\unit[1,9]{V}](../_images/math/ff0c3f041cbe3f458da501d2e4e7007dc5a5da6a.png) die Stromstärke
die Stromstärke
![\unit[20]{mA}](../_images/math/363d7fee9882e8356537c82e4e6944546447668c.png) betragen soll?
betragen soll?Die LED wird ab
![\unit[1,9]{V}](../_images/math/ff0c3f041cbe3f458da501d2e4e7007dc5a5da6a.png) leitfähig; bei nur geringfügig höheren
Spannungen steigt die Stromstärke gemäß der gewöhnlichen Diodenkennlinie sehr
schnell an. Man kann folglich damit rechnen, dass der Spannungsabfall an der LED
immer rund
leitfähig; bei nur geringfügig höheren
Spannungen steigt die Stromstärke gemäß der gewöhnlichen Diodenkennlinie sehr
schnell an. Man kann folglich damit rechnen, dass der Spannungsabfall an der LED
immer rund ![\unit[1,9]{V}](../_images/math/ff0c3f041cbe3f458da501d2e4e7007dc5a5da6a.png) beträgt, unabhängig von der Stromstärke. Am
Vorwiderstand muss somit bei einer anliegenden Gesamtspannung von
beträgt, unabhängig von der Stromstärke. Am
Vorwiderstand muss somit bei einer anliegenden Gesamtspannung von
![\unit[9]{V}](../_images/math/d72464e9d3f0af08777997e0da6e5a1148bb200d.png) eine Teilspannung von
eine Teilspannung von ![U_1=\unit[7,1]{V}](../_images/math/bb09d99bc84014ba4ca686f73a6ee9a25a66d811.png) abfallen.
abfallen.Da zudem die Stromstärke im Vorwiderstand
![I_1 = I_{\mathrm{ges}} =
\unit[20]{mA}](../_images/math/b5a61d00ea0b98d765b2146a6755a42094e17eb2.png) betragen soll, kann der Wert
betragen soll, kann der Wert 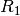 des Vorwiderstands
gemäß dem Ohmschen Gesetz berechnet werden:
des Vorwiderstands
gemäß dem Ohmschen Gesetz berechnet werden:![R_1 = \frac{U_1}{I_1} = \frac{\unit[7,1]{V}}{\unit[0,02]{A}} \approx
\unit[355]{\Omega}](../_images/math/d8b7a3c03bc819c6c792886906b648179d2140f4.png)
Hat man einen solchen Widerstand nicht als Bauteil vorliegen, so kann man entweder den nächst größeren wählen, oder einen regelbaren Widerstand (ein Potentiometer) verwenden.
Man kann in Schaltung LED mit Vorwiderstand
den Taster 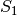 auch durch zwei offene Leiter-Enden ersetzen, um einen
„Durchgangsprüfer“ zu erhalten. Hält man diese an die Kontaktstellen eines
anderen leitenden Bauteils, beispielsweise an eine andere Leuchtdiode, einen
(nicht zu großen) Widerstand oder an eine kleine Glühbirne, so leuchtet die
Leuchtdiode
auch durch zwei offene Leiter-Enden ersetzen, um einen
„Durchgangsprüfer“ zu erhalten. Hält man diese an die Kontaktstellen eines
anderen leitenden Bauteils, beispielsweise an eine andere Leuchtdiode, einen
(nicht zu großen) Widerstand oder an eine kleine Glühbirne, so leuchtet die
Leuchtdiode 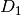 auf, sofern das Bauteil intakt ist. Bei zu großen
Widerständen oder unterbrochenen Kontaktstellen – beispielsweise einem intakten
Kondensator oder einer durchgebrannten Sicherung – bleibt
auf, sofern das Bauteil intakt ist. Bei zu großen
Widerständen oder unterbrochenen Kontaktstellen – beispielsweise einem intakten
Kondensator oder einer durchgebrannten Sicherung – bleibt 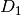 hingegen
dunkel.
hingegen
dunkel.
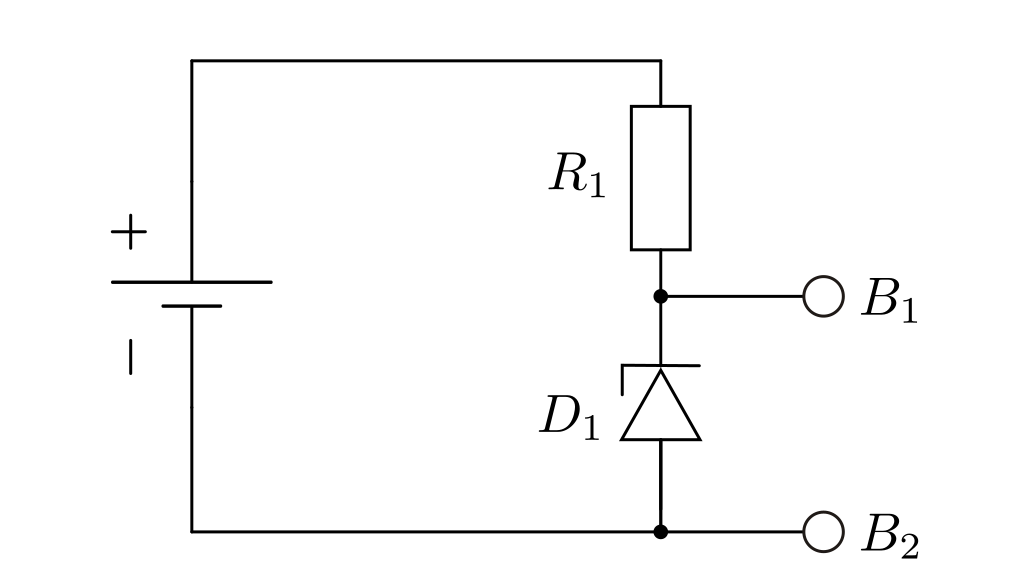
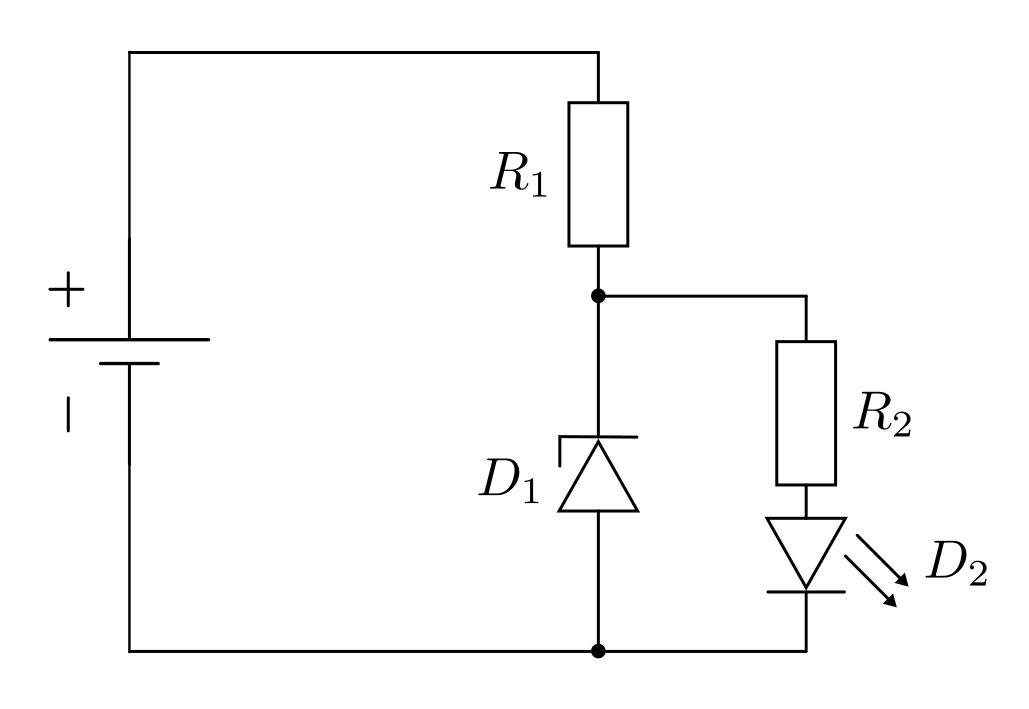
Spannungsregelung mit Z-Dioden¶
Solange die Quellspannung 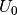 unterhalb der Durchbruchspannung der
Zenerdiode
unterhalb der Durchbruchspannung der
Zenerdiode 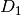 bleibt, liegt zwischen den Anschlüssen
bleibt, liegt zwischen den Anschlüssen 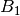 und
und
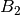 ebenfalls die Spannung
ebenfalls die Spannung 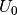 an. Steigt
an. Steigt 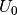 hingegen
über die Durchbruchspannung von
hingegen
über die Durchbruchspannung von 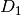 , so bleibt die Spannung zwischen
, so bleibt die Spannung zwischen
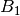 und
und 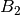 beim Wert der Durchbruchspannung von
beim Wert der Durchbruchspannung von 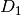 ;
die restliche Spannung fällt am Widerstand
;
die restliche Spannung fällt am Widerstand 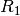 ab.
ab.
Der Grund dafür liegt darin, dass 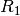 und
und 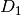 einen
Spannungsteiler bilden, wobei an
einen
Spannungsteiler bilden, wobei an 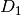 maximal die Durchbruchspannung und
an
maximal die Durchbruchspannung und
an 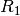 die restliche Spannung abfällt.
die restliche Spannung abfällt.
Allgemein gilt bei der Verwendung von 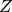 -Dioden:
-Dioden:
- Die Ausgangsspannung wird durch die Durchbruchspannung der
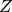 -Diode
bestimmt.
-Diode
bestimmt. - Die Eingangsspannung muss größer als die Ausgangsspannung sein.
- Je größer die Differenz zwischen Eingangs- und Ausgangsspannung ist, desto weniger wird die Ausgangsspannung durch Schwankungen der Eingangsspannung beeinflusst.
- Die Verlust-Leistung
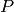 an einer
an einer 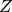 -Diode ist am größten, wenn
sich diese im Leerlauf befindet (also kein Verbraucher angeschlossen ist).
-Diode ist am größten, wenn
sich diese im Leerlauf befindet (also kein Verbraucher angeschlossen ist).
Anhand des folgenden Beispiels soll gezeigt werden, inwiefern sich eine
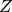 -Diode als Spannungs-Stabilisator einsetzen lässt. Betrieben werden
soll eine eine rote LED mit einer Betriebsspannung von
-Diode als Spannungs-Stabilisator einsetzen lässt. Betrieben werden
soll eine eine rote LED mit einer Betriebsspannung von ![U_{\mathrm{LED}} =
\unit[1,9]{V}](../_images/math/2806b57cefe8f207915ccf723a0cb96681434c83.png) und einer Soll-Stromstärke von
und einer Soll-Stromstärke von ![\unit[20]{mA}](../_images/math/363d7fee9882e8356537c82e4e6944546447668c.png) ; die
; die
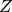 -Diode habe eine Durchbruch-Spannung von
-Diode habe eine Durchbruch-Spannung von ![U_{\mathrm{ZD}} =
\unit[5,6]{V}](../_images/math/fb4f75e9359dab467f2a423bd5fce4ff855de849.png) .
.
Am Widerstand 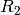 muss die Differenz dieser beider Spannungen abfallen,
also
muss die Differenz dieser beider Spannungen abfallen,
also ![\unit[3,7]{V}](../_images/math/97b9d912e7ac130b82afa375aa985a7724d3b383.png) . Für den Wert des Widerstands
. Für den Wert des Widerstands 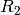 ergibt sich
damit:
ergibt sich
damit:
![R_2 = \frac{U_{\mathrm{ZD}} - U_{\mathrm{LED}}}{I_{\mathrm{LED}}} =
\frac{\unit[5,6]{V} - \unit[1,9]{V}}{\unit[0,02]{A}} \approx
\unit[185]{\Omega}](../_images/math/1cc6bd590a00f714ae65d374bf0d79a8b8c28d35.png)
Damit die LED keinen Schaden nehmen kann, wird man sich für den nächst größeren
verfügbaren Widerstand entscheiden, also beispielsweise
![R_2=\unit[220]{\Omega}](../_images/math/31319dc80dfc62d8a15723c323253696f4d9e43a.png) wählen. Um die Größe es Widerstands
wählen. Um die Größe es Widerstands 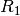 berechnen zu können, muss man die Gesamt-Stromstärke kennen; diese setzt sich
zusammen aus dem Strom
berechnen zu können, muss man die Gesamt-Stromstärke kennen; diese setzt sich
zusammen aus dem Strom ![I_{\mathrm{LED}} = \unit[0,02]{A}](../_images/math/f850c78c45a0fcf40919614c7122f2bd230b8d11.png) und dem
Mindeststrom durch die
und dem
Mindeststrom durch die 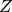 -Diode. Letzterer kann aus dem Datenblatt der
Diode entnommen werden, oder gemäß folgender Formel abgeschätzt werden, wenn man
zusätzlich zur Spannung
-Diode. Letzterer kann aus dem Datenblatt der
Diode entnommen werden, oder gemäß folgender Formel abgeschätzt werden, wenn man
zusätzlich zur Spannung 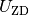 auch die Leistung
auch die Leistung
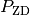 der
der 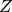 -Diode kennt:
-Diode kennt:
![I_{\mathrm{ZD,min}} = 10\% \cdot \frac{P_{\mathrm{ZD}}}{U_{\mathrm{ZD}}} =
0,1 \cdot \frac{\unit[0,5]{W}}{\unit[5,6]{V}} \approx \unit[9]{mA}](../_images/math/7063f90ead2cdd436d1fe31c15da5fa0aa9ac073.png)
Hat die 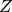 -Diode beispielsweise eine angegebene Leistung von
-Diode beispielsweise eine angegebene Leistung von
![\unit[0,5]{W}](../_images/math/6eaee0b732f47d228b167a991b1fb2eea375a6bb.png) , so erhält man nach obiger Abschätzung einen Mindeststrom
von
, so erhält man nach obiger Abschätzung einen Mindeststrom
von ![\unit[0,009]{A}](../_images/math/926e9346e26797a340de36de908b33098e12721d.png) durch die
durch die 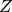 -Diode; für den Gesamtstrom
erhält man somit
-Diode; für den Gesamtstrom
erhält man somit ![I_{\mathrm{ges}} \ge \unit[29]{mA}](../_images/math/80170afcc94dcd2c6855224aa375686e99bee2b4.png) .
.
Angenommen, die maximale Eingangs-Spannung beträgt ![\unit[15]{V}](../_images/math/b785155c106d74127e2ee32a2869918300202e0c.png) . Diese
Spannung würde bedeuten, dass am Widerstand
. Diese
Spannung würde bedeuten, dass am Widerstand 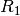 eine Spannung von
eine Spannung von
![U_1=\unit[(15-5,6)]{V}](../_images/math/0dff7b68cee1c8a4ca91b75bcdb4a2763d929446.png) abfallen muss. Für den Wert des Widerstands
abfallen muss. Für den Wert des Widerstands
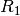 ergibt sich damit:
ergibt sich damit:
![R_1 = \frac{U_1}{I_{\mathrm{ges}}} =
\frac{\unit[(15,0-5,6)]{V}}{\unit[0,029]{A}} \approx \unit[324]{\Omega}](../_images/math/5fe36843349673146f8e86ac8d1f08cbe5dd80d8.png)
Ein üblicher ![\unit[330]{\Omega}](../_images/math/13a16258e14d477e33261ad50332f2d7fd4f2f51.png) -Widerstand sollte also als Wahl für
-Widerstand sollte also als Wahl für
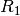 geeignet sein. Bei einer Betriebspannung von
geeignet sein. Bei einer Betriebspannung von ![\unit[15]{V}](../_images/math/b785155c106d74127e2ee32a2869918300202e0c.png) wird der Widerstand
wird der Widerstand 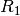 allerdings stark belastet; die an
allerdings stark belastet; die an 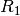 in
Wärme umgesetzte Leistung
in
Wärme umgesetzte Leistung 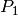 beträgt in diesem Fall:
beträgt in diesem Fall:
![P_1 = U_1 \cdot I_{\mathrm{ges}} = \unit[(15,0-5,6)]{V} \cdot \unit[0,029]{A}
\approx \unit[0,273]{W}](../_images/math/c46ba82645e2a208eb607de6bcc01b28c2a95cff.png)
Sicherheitshalber sollte also anstelle eines normalen
![\unit[1/4]{W}](../_images/math/01840ecaacd1a6c1181a31f154e9cd78e1415794.png) -Widerstands ein stärker belastbarer
-Widerstands ein stärker belastbarer
![\unit[1/2]{W}](../_images/math/ca7bc704be53237bf82411c703d14381fe290440.png) -Widerstand verwendet werden.
-Widerstand verwendet werden.
Durch die Verwendung der 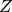 -Diode kann die LED mit den übrigen oben
berechneten Bauteilen nun mit einer Versorgungsspannung zwischen
mindestens
-Diode kann die LED mit den übrigen oben
berechneten Bauteilen nun mit einer Versorgungsspannung zwischen
mindestens ![\unit[5,6]{V}](../_images/math/4cb82bd147c7387851431ce80d35079c2550d836.png) (der Mindest-Spannung der
(der Mindest-Spannung der 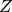 -Diode) und
maximal
-Diode) und
maximal ![\unit[15,0]{V}](../_images/math/4161438c3156aa9ac1c08ae687701c036f46c4f3.png) betrieben werden.[2]
betrieben werden.[2]
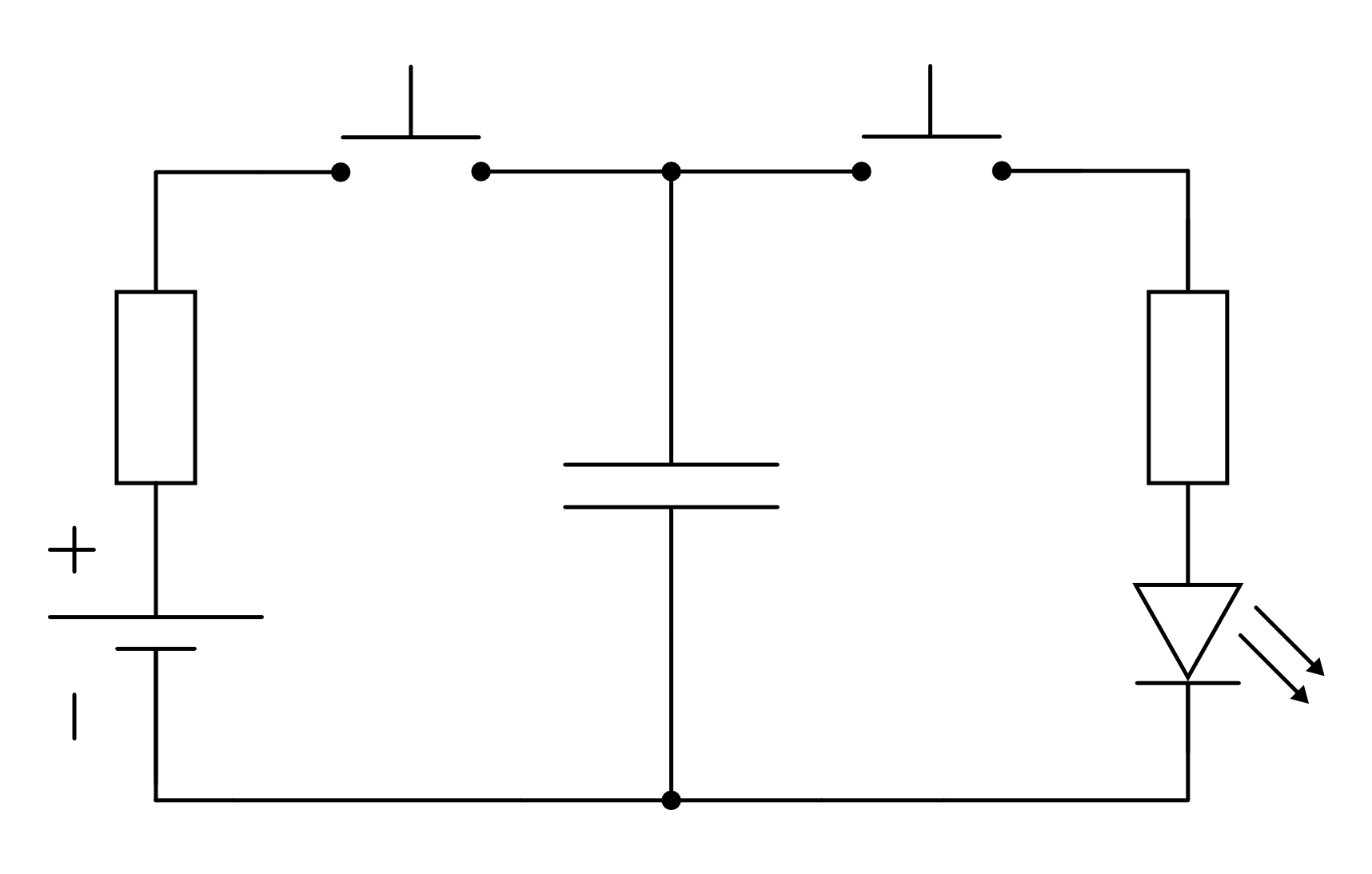
Kondensator-Grundfunktion¶
Kondensatoren haben die Fähigkeit elektrische Ladung zu speichern und sie langsam wieder abzugeben. Eine einfache Schaltung, die diese Funktionsweise veranschaulicht, ist folgende:
Die Schaltung funktioniert folgendermaßen:
- Betätigt man nur den linken Taster, so lädt sich der Kondensator auf. Ist er vollständig geladen, fließt (fast) kein weiterer Strom.[3]
- Betätigt man nur den rechten Taster, so kann sich der Kondensator über die Leuchtdiode und ihren Vorwiderstand entladen. Die LED leuchtet kurzzeitig auf, wobei ihre Leuchtstärke ebenso wie der Entladestrom des Kondensators beständig abnimmt.
Betätigt man beide Taster, oder sind keine Taster vorhanden, so wird der Kondensator geladen und die LED leuchtet. Wird die Stromquelle abgetrennt, so erlischt die LED je nach Kapazität des eingebauten Kondensators mehr oder weniger schnell.
Transistor-Grundschaltungen¶
Ein Transistor kann, je nach Schaltungsart, als elektronischer Schalter oder als regelbarer Verstärker eingesetzt werden.
Darlington-Schaltung¶
Bei einer Darlington-Schaltung werden zwei Transistoren so eingesetzt, dass der
erste als „Vorverstärker“ für den zweiten wirkt. Auf diese Weise multiplizieren
sich ihre Verstärkungsfaktoren; es genügt folglich bereits eine extrem kleine
Stärke an der Basis von 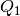 bereits aus, um über
bereits aus, um über 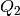 eine Last
(in diesem Fall die LED
eine Last
(in diesem Fall die LED 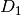 mit dem Vorwiderstand
mit dem Vorwiderstand 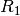 ) zu
schalten.
) zu
schalten.
Beträgt die Versorgungsspannung ![U=\unit[9]{V}](../_images/math/9a932c6c6e70a67ced791c8b82c9ac1dcdb6a8a7.png) , so sind
, so sind
![R_1=\unit[470]{\Omega}](../_images/math/1970ba664a1e38a78e32b0df7a79db2bf6b9eea7.png) und
und ![R_2 \ge \unit[1]{k \Omega}](../_images/math/78e0e9009ca61845d29ea2c5d55af99a2d700ad0.png) geeignete
Widerstandswerte. Anstelle des Tasters kann man auch einen (oder sogar zwei
separate) Finger sowie verschiedene Materialproben zum Schließen der Kontakte
verwenden.
geeignete
Widerstandswerte. Anstelle des Tasters kann man auch einen (oder sogar zwei
separate) Finger sowie verschiedene Materialproben zum Schließen der Kontakte
verwenden.
Hat beispielsweise der erste Transistor 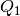 einen Verstärkungsfaktor von
einen Verstärkungsfaktor von
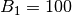 , so bewirkt der dort hinein fließende Basis-Strom einen
, so bewirkt der dort hinein fließende Basis-Strom einen
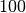 -fach größeren Kollektor-Emitter-Strom in
-fach größeren Kollektor-Emitter-Strom in 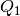 ; dieser
wiederum entspricht dem Basis-Strom von
; dieser
wiederum entspricht dem Basis-Strom von 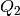 . Hat auch der Transistor
. Hat auch der Transistor
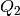 einen Verstärkungsfaktor von
einen Verstärkungsfaktor von 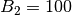 , so ergibt sich
insgesamt ein Verstärkungsfaktor von
, so ergibt sich
insgesamt ein Verstärkungsfaktor von 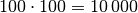 .
.
Dadurch, dass beide Kollektoren miteinander verbunden sind, benötigt der
Transistor 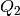 keinen Strom begrenzenden Widerstand. Wird nämlich der
Kollektor-Emitter-Strom
keinen Strom begrenzenden Widerstand. Wird nämlich der
Kollektor-Emitter-Strom  von
von 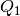 sehr hoch, dann
schaltet der zweite Transistor
sehr hoch, dann
schaltet der zweite Transistor 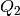 komplett durch; ist dies der Fall, so
beträgt die Spannung zwischen dessen Kollektor
komplett durch; ist dies der Fall, so
beträgt die Spannung zwischen dessen Kollektor 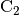 und Emitter
und Emitter
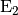 nur noch etwa
nur noch etwa ![\unit[0,2]{V}](../_images/math/ba5239b7b6dd44ad959eb036e7f124d6cf596bb2.png) . Dies wiederum hat zur
Folge dass nicht mehr die erforderlichen
. Dies wiederum hat zur
Folge dass nicht mehr die erforderlichen ![\unit[0,6]{V}](../_images/math/6294a750ecd796fdd4e09d8751db6e77ee20e80e.png) an der Basis von
an der Basis von
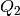 anliegen können.
anliegen können.
Der Transistor 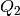 wird somit nie komplett durchschalten: Die Schaltung
reguliert sich vielmehr von selbst, so dass zwischen
wird somit nie komplett durchschalten: Die Schaltung
reguliert sich vielmehr von selbst, so dass zwischen 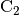 und
und
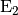 ein Spannungsabfall von etwa
ein Spannungsabfall von etwa ![\unit[0,8]{V}](../_images/math/8ab3e1436dad8f6e884d6d436bafc55e2d984ff6.png) bestehen
bleibt (
bestehen
bleibt (![\unit[0,6]{V}](../_images/math/6294a750ecd796fdd4e09d8751db6e77ee20e80e.png) für die
für die 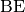 -Strecke von
-Strecke von
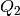 und
und ![\unit[0,2]{V}](../_images/math/ba5239b7b6dd44ad959eb036e7f124d6cf596bb2.png) für die
für die 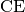 -Strecke von
-Strecke von
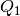 ).
).
Es gibt auch so genannte „Darlington-Transistoren“, in denen die obige Anordnung
der beiden Transistoren 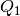 und
und 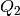 bereits in einem einzigen
Bauteil vereint ist.
bereits in einem einzigen
Bauteil vereint ist.
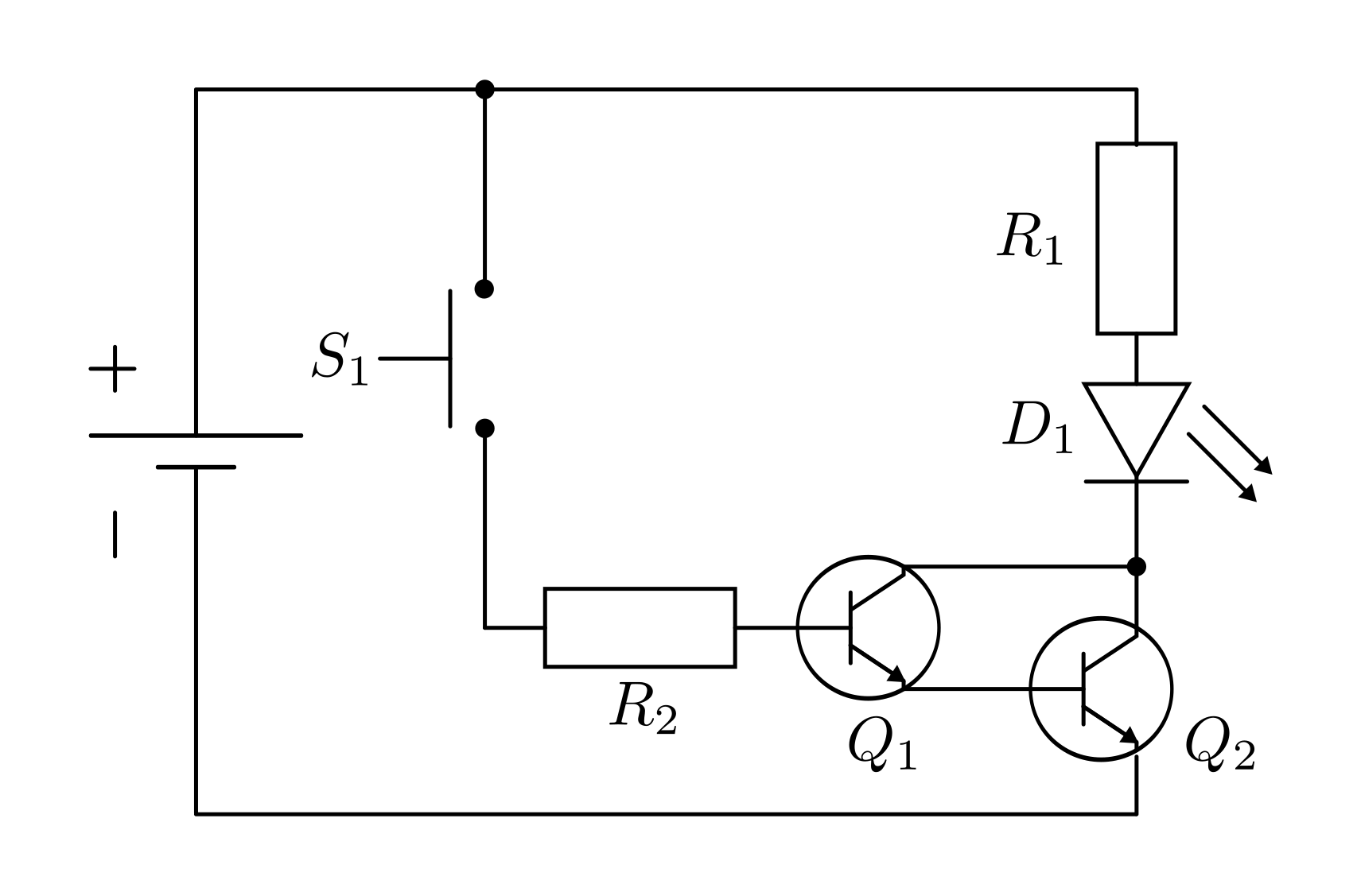
Transistor als Aus-Schalter¶
Der folgende Schaltplan zeigt, wie man einen Transistor auch als Aus-Schalter (Öffner) verwenden kann.
Beträgt die Versorgungsspannung ![U=\unit[9]{V}](../_images/math/9a932c6c6e70a67ced791c8b82c9ac1dcdb6a8a7.png) , so sind
, so sind
![R_1=\unit[470]{\Omega}](../_images/math/1970ba664a1e38a78e32b0df7a79db2bf6b9eea7.png) und
und ![R_2 = R_3 = \unit[1]{k \Omega}](../_images/math/6b4a0156c6db27330553026bb768d242694a7c2c.png) geeignete Widerstandswerte.
geeignete Widerstandswerte.
Wird der Taster 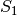 nicht gedrückt, so erhält der Transistor
nicht gedrückt, so erhält der Transistor 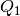 keinen Strom an der Basis. Der Transistor
keinen Strom an der Basis. Der Transistor 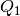 sperrt in diesem Fall, und
die LED
sperrt in diesem Fall, und
die LED 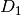 leuchtet (da der Transistor
leuchtet (da der Transistor 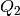 einen Basis-Strom
durch
einen Basis-Strom
durch 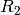 erhält). Drückt man hingegen den Taster
erhält). Drückt man hingegen den Taster 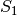 , so geht
die LED aus.
, so geht
die LED aus.
Durch das Drücken des Tasters 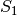 schaltet der Transistor
schaltet der Transistor 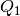 durch; der Spannungsabfall gegenüber dem Ground-Niveau (
durch; der Spannungsabfall gegenüber dem Ground-Niveau (GND) beträgt somit
nur noch ![\unit[0,2]{V}](../_images/math/ba5239b7b6dd44ad959eb036e7f124d6cf596bb2.png) . An der Basis von
. An der Basis von 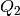 liegt somit
ebenfalls nur noch eine Spannung von
liegt somit
ebenfalls nur noch eine Spannung von ![\unit[0,2]{V}](../_images/math/ba5239b7b6dd44ad959eb036e7f124d6cf596bb2.png) (gegenüber
(gegenüber GND)
an; dies genügt jedoch nicht, um einen signifikanten Stromfluss durch die
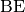 -Diode von
-Diode von 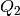 zu erreichen. Der Strom durch
zu erreichen. Der Strom durch
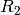 fließt somit über
fließt somit über 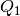 an
an GND abgeleitet, und 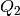 sperrt.[4]
sperrt.[4]
Emitterschaltung¶
Bei der so genannten Emitter-Schaltung ist der Emitter des Transistors direkt mit dem Ground-Anschluss verbunden. Bei einer derartigen Schaltung wird der Transistor nicht als Schalter, sondern als Verstärker eingesetzt.
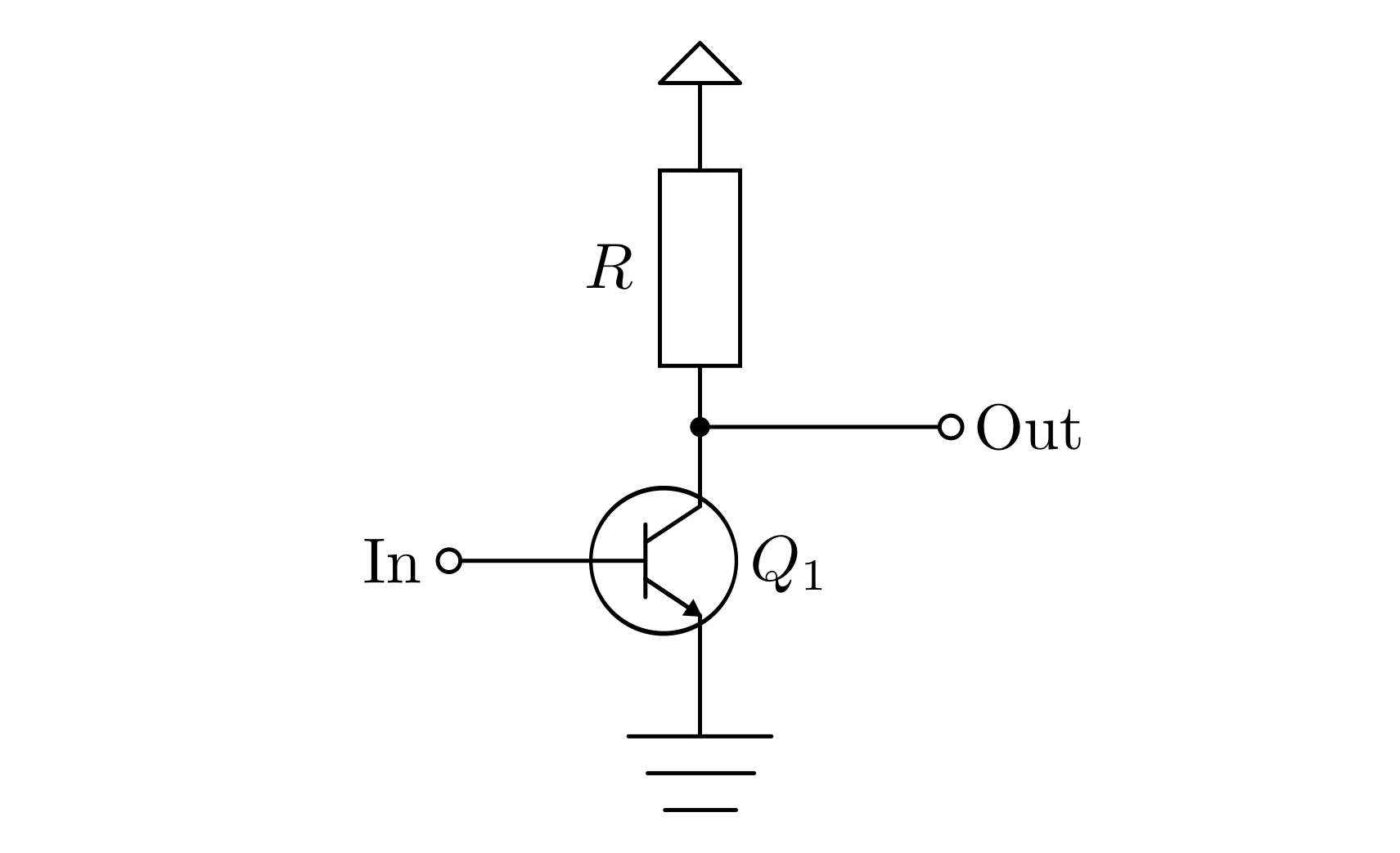
Eine einfache Emitter-Schaltung, wie sie in der folgenden Abbildung dargestellt ist, stellt einen invertierenden Verstärker dar. Wird am Eingang (der Basis des Transistors) die anliegende Spannung etwas erhöht, so geht die am Ausgang anliegende Spannung stark zurück. Die verstärkende Wirkung liegt darin, dass eine kleine Änderung am Eingang eine große Änderung am Ausgang bewirkt; die invertierende Wirkung liegt darin, dass eine Erhöhung des Potentials am Eingang eine Reduzierung des Potentials am Ausgang zur Folge hat.
In diesem Schaltplan wird das nach oben zeigende Dreieck als Symbol für den Anschluss der Spannungsversorgung verwendet. Die Funktionsweise der Schaltung ist folgendermaßen zu erklären:
- Liegt an der Basis des Transistors eine verhältnismäßig hohe Spannung an, so
wird die Kollektor-Emitter-Strecke des Transistors leitend. Es fließt dadurch
viel Strom durch den Transistor und somit auch durch den Widerstand
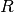 ;
an diesem ergibt sich als Folge davon aufgrund des Ohmschen Gesetzes
;
an diesem ergibt sich als Folge davon aufgrund des Ohmschen Gesetzes 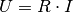 auch ein hoher Spannungsabfall. Am Ausgang ist die Spannung
gegenüber dem Spannungsanschluss deutlich verringert.
auch ein hoher Spannungsabfall. Am Ausgang ist die Spannung
gegenüber dem Spannungsanschluss deutlich verringert. - Liegt an der Basis des Transistors keine Spannung an, so sperrt der
Transistor; es fließt somit kein Strom durch die Kollektor-Emitter-Strecke und
folglich auch nur verhältnismäßig wenig Strom durch den Widerstand
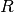 (abhängig von der restlichen Schaltung am Ausgang). Folglich entspricht die
Spannung weitgehend der Spannung am Spannungsanschluss.
(abhängig von der restlichen Schaltung am Ausgang). Folglich entspricht die
Spannung weitgehend der Spannung am Spannungsanschluss.
Eine leichte Änderung der Basis-Spannung bewirkt bei einem Transistor sehr große
Änderungen bezüglich der fließenden Stromstärke; wird beispielsweise bei einem
BC547 die Basis-Spannung um 1/6 erhöht, so ergibt sich ein rund 20-fach größerer
Kollektor-Strom; man nutzt den Transistor also als Spannungs-Strom-Wandler. Den
Widerstand 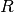 hingegen kann man wiederum als Strom-Spannungs-Wandler
ansehen: Schickt man einen Strom durch einen Widerstand hindurch, so erhält man
eine Spannung beziehungsweise einen Spannungsabfall. Da das Zahlen-Verhältnis
hingegen kann man wiederum als Strom-Spannungs-Wandler
ansehen: Schickt man einen Strom durch einen Widerstand hindurch, so erhält man
eine Spannung beziehungsweise einen Spannungsabfall. Da das Zahlen-Verhältnis
 (in Standard-Einheiten) üblicherweise deutlich größer als
(in Standard-Einheiten) üblicherweise deutlich größer als
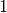 ist, kann man mittels des Widerstands wiederum aus einigen Miliampere
an Stromfluss ein paar Volt als Spannungsänderung hervorrufen.
ist, kann man mittels des Widerstands wiederum aus einigen Miliampere
an Stromfluss ein paar Volt als Spannungsänderung hervorrufen.
Die oben beschriebene Emitter-Schaltung funktioniert nur dann sinnvoll, wenn nur ein vernachlässigbar geringer Strom durch den Ausgang fließt; die am Ausgang angebrachte Schaltung muss also „hochohmig“ sein. Emitter-Schaltungen werden am Häufigsten zur Verstärkung von Audio-Signalen verwendet, beispielsweise als Vorverstärker für Mikrophone. Zur Weiterverarbeitung der Signale werden dann beispielsweise Operationsverstärker genutzt.
… to be continued …
Anmerkungen:
| [1] | Diese Formel erhält man für eine Parallelschaltung zweier Widerstände, indem man die Brüche auf der rechten Seite der Gleichung durch Erweitern zusammenfasst:
Auf beiden Seiten der Gleichung steht nun je ein einzelner Bruchterm. Da beide gleich sind, müssen auch die jeweiligen Kehrbrüche zueinander gleich sein. Man erhält damit für die Parallelschaltung zweier Widerstände:
Für drei oder mehr Widerstände ist diese Berechnungs-Formel hingegen nicht gültig! |
| [2] | Bei einer Versorgungsspannung von nur ![\unit[5,6]{V}](../_images/math/4cb82bd147c7387851431ce80d35079c2550d836.png) leuchtet die
LED allerdings nur noch sehr schwach: Die Z-Diode spielt bei diesem Wert
nämlich, so dass leuchtet die
LED allerdings nur noch sehr schwach: Die Z-Diode spielt bei diesem Wert
nämlich, so dass 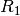 und und 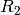 als Reihenschaltung einen
Gesamt-Vorwiderstand von als Reihenschaltung einen
Gesamt-Vorwiderstand von 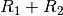 , also rund , also rund
![\unit[500]{\Omega}](../_images/math/91bf304b1715b3d1a913fbf6ef235374bd475e7e.png) haben. Das bedeutet bei einem angenommenen
Spannungsabfall von haben. Das bedeutet bei einem angenommenen
Spannungsabfall von ![\unit[1,9]{V}](../_images/math/ff0c3f041cbe3f458da501d2e4e7007dc5a5da6a.png) an der LED einen Spannungsabfall
von an der LED einen Spannungsabfall
von ![\unit[(5,6-1,9)]{V}= \unit[3,7]{V}](../_images/math/7072f4b86f1c827363c2ca9283d43e74c800faf0.png) am Vorwiderstand, so dass sich
eine Stromstärke von nur am Vorwiderstand, so dass sich
eine Stromstärke von nur ![\unit[3,7]{V} / \unit[500]{\Omega} \approx
\unit[7,4]{mA}](../_images/math/3211316438e7514d9887543fce8fb255f403ede6.png) einstellen wird. Diese Stromstärke ist, verglichen mit einer
„normalen“ LED-Stromstärke von einstellen wird. Diese Stromstärke ist, verglichen mit einer
„normalen“ LED-Stromstärke von ![\unit[20]{mA}](../_images/math/363d7fee9882e8356537c82e4e6944546447668c.png) , verhältnismäßig
gering. , verhältnismäßig
gering. |
| [3] | Da es keinen perfekten Isolator gibt, weisen Kondensatoren stets eine gewisse Selbstentladung auf, wobei Ladung von der einen Plattenseite zur anderen fließt. Ist der Kondensator noch mit einer Stromquelle verbunden, so fließt diese Ladung von der Stromquelle auf den Kondensator nach. |
| [4] | Für Um doch einen Darlington-Transistor verwenden zu können, müsste man zwischen
dem Emitter von |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.

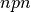 -Transistoren.
-Transistoren.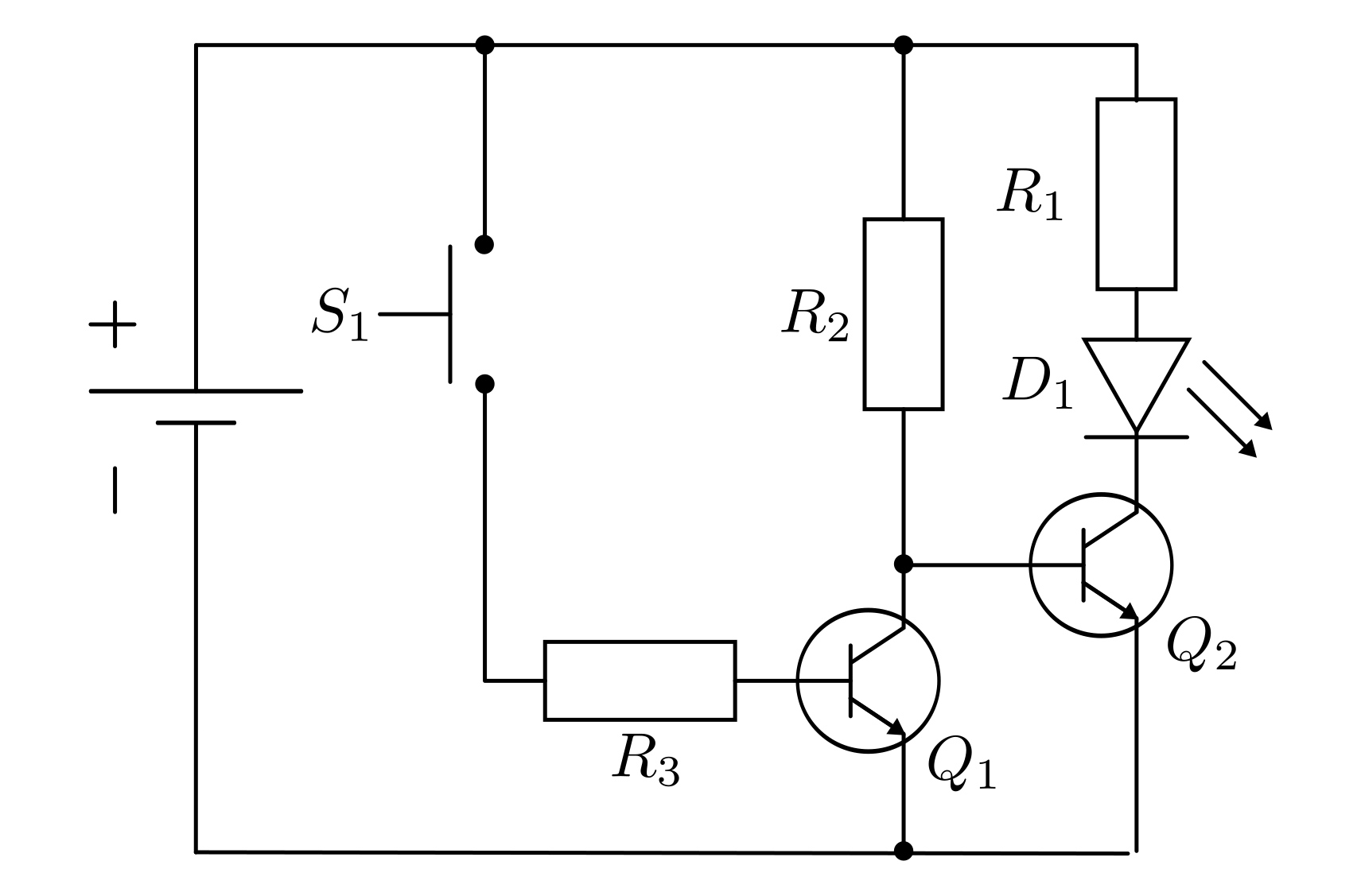
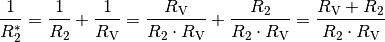
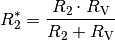
![\unit[1,2]{V}](../_images/math/a663599199c66db83de898860ec11ed39153df12.png) an der
Basis von
an der
Basis von