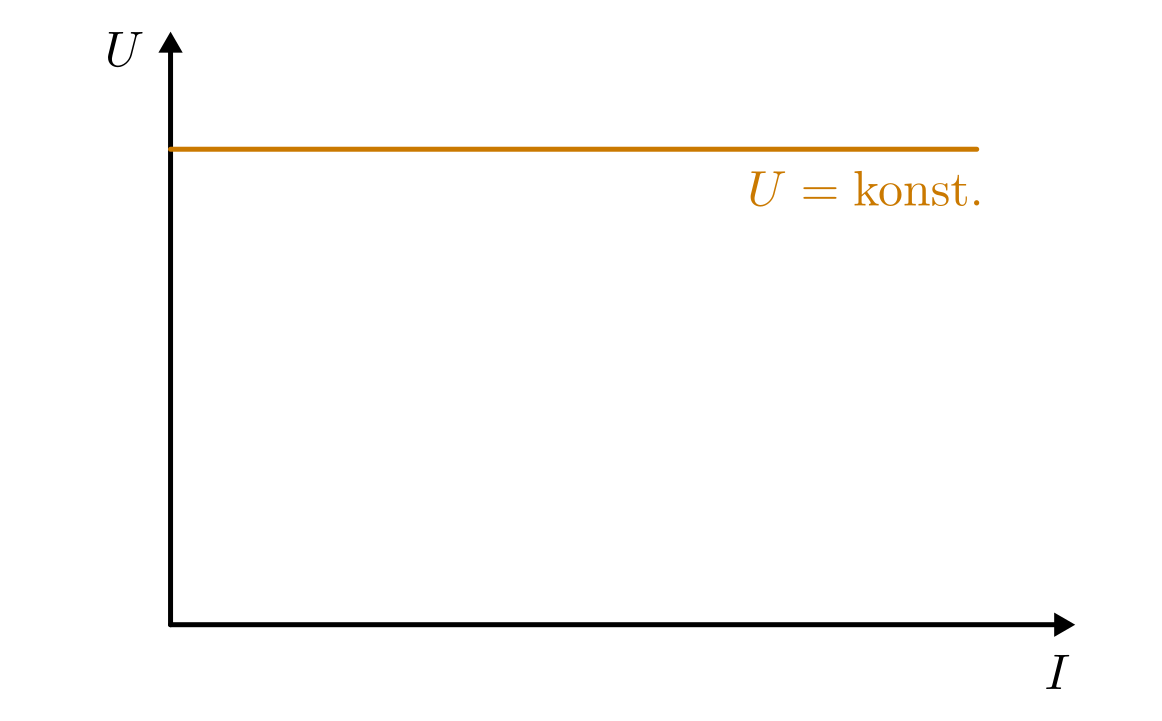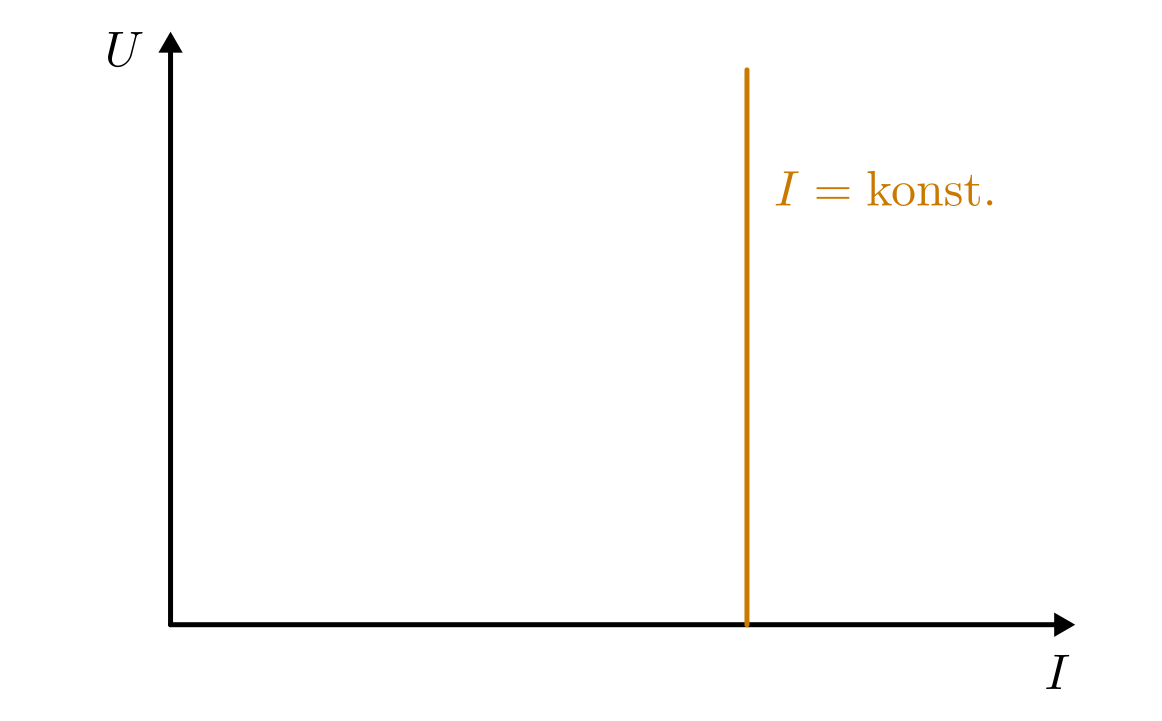Spannungs- und Stromquellen¶
Damit in einem Stromkreis ein elektrischer Strom fließen kann, muss eine elektrische Spannung anliegen. Umgangssprachlich wird diese von einer „Stromquelle“ bereitgestellt; in der Elektronik unterscheidet man hingegen zwischen „Spannungsquellen“ und „Stromquellen“:
Eine ideale Spannungsquelle liefert eine konstanten Spannungswert, unabhängig von der Größe der Stromstärke, die der Quelle entnommen wird.
Eine ideale Stromquelle liefert stets die gleiche Stromstärke; die zum Liefern dieser Stromstärke nötige Spannung wird von der Stromquelle automatisch geregelt.
Beide Typen sind idealisierte Modelle, die es in der Realität so nicht geben
kann: Könnte beispielsweise bei einer idealen Spannungsquelle tatsächlich ein
beliebig großer Strom entnommen werden, so würde auch die bereitgestellte
Leistung gemäß der Formel 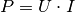 beliebig groß werden. Bei realen
Spannungsquellen sinkt daher die Spannung, wie unten im Exkurs:
Innenwiderstand realer Spannungsquellen näher beschrieben wird, bei zunehmend größeren Stromstärken
ab; gleichermaßen können reale Stromquellen keine beliebig großen Spannungswerte
liefern, die bei großen Last-Widerständen nötig wären, um die Soll-Stromstärke
aufrecht zu erhalten.
beliebig groß werden. Bei realen
Spannungsquellen sinkt daher die Spannung, wie unten im Exkurs:
Innenwiderstand realer Spannungsquellen näher beschrieben wird, bei zunehmend größeren Stromstärken
ab; gleichermaßen können reale Stromquellen keine beliebig großen Spannungswerte
liefern, die bei großen Last-Widerständen nötig wären, um die Soll-Stromstärke
aufrecht zu erhalten.
Die idealen Modelle werden aufgrund ihrer Einfachheit dennoch verwendet, da sie oftmals die realen Vorgänge bereits gut genug beschreiben können; ergeben sich bei Verwendung dieser einfachen Modelle Widersprüche oder (bei Rechnungen) unrealistische Werte, so müssen diese – wie am am Ende dieses Kapitels näher beschrieben – nachgebessert werden.
Spannungsquellen mit Gleichspannung¶
Am Minuspol einer Spannungsquelle besteht ein Elektronenüberschuss, am Pluspol ein Elektronenmangel. Beide Zustände werden durch Vorgänge im Inneren der Spannungsquelle erzeugt beziehungsweise aufrecht erhalten.
Batterien
Batterien haben chemische Energie im Inneren gespeichert und sind in der Lage, diese in Form von elektrischer Energie freizusetzen. Entladene Batterien, deren gespeicherte Energiemenge verbraucht ist, müssen an einer Wertstoff-Sammelstelle abgegeben oder in speziell dafür aufgestellte Container geworfen werden.[1] Auf diese Weise können die Bestandteile der Batterie (weitgehend) wieder verwertet werden, und es gelangen zumindest weitaus weniger Giftstoffe in die Umwelt.
Batterien können nicht wieder aufgeladen werden und weisen somit gegenüber Akkumulatoren sowohl aus wirtschaftlicher wie aus ökologischer Sicht erhebliche Nachteile auf. Sie werden normalerweise nur dann in mobilen Bereichen eingesetzt, wenn eine vergleichsweise höhere Speicherkapazität und/oder eine geringfügig höhere Leistungsabgabe zwingend erforderlich sind.
Akkumulatoren
Akkumulatoren (auch „Akkus genannt) sind „wiederaufladbare Batterien“. Beim Aufladen wird elektrische Energie in Form von chemischer Energie durch die Umwandlung von Stoffen im Inneren des Akkus gespeichert. Beim Entladen läuft der chemische Prozess in umgekehrter Richtung ab, und es wird elektrische Energie freigegeben.
Beispiele:
Blei-Akkumulator:
Im ungeladenen Zustand bestehen die Platten aus Bleisulfat
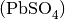 . Beim Aufladen reagiert die positive Elektrode zu
Bleioxid
. Beim Aufladen reagiert die positive Elektrode zu
Bleioxid 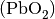 und die negative Elektrode zu Blei
und die negative Elektrode zu Blei
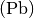 . Als Elektrolyt wird verdünnte Schwefelsäure verwendet.
. Als Elektrolyt wird verdünnte Schwefelsäure verwendet.Die Spannung je Zelle beträgt etwa
![\unit[2]{V}](../_images/math/162814019d4f082b76b6a6d75cacbb2a11431a3f.png) . In handelsüblichen
Blei-Akkumulatoren sind meistens sechs Zellen in einer Reihenschaltung
miteinander verbunden, so dass an den Anschlüssen eine Spannung von
. In handelsüblichen
Blei-Akkumulatoren sind meistens sechs Zellen in einer Reihenschaltung
miteinander verbunden, so dass an den Anschlüssen eine Spannung von
![\unit[12]{V}](../_images/math/6727cf2261a87b8820671c96ceb116cfe26cc0e4.png) abgegriffen werden kann.
abgegriffen werden kann.Nickel-Eisen-Akkumulator:
Als Elektrolyt wird verdünnte Kali-Lauge verwendet; die Spannung je Zelle beträgt etwa
![\unit[1,2]{V}](../_images/math/a663599199c66db83de898860ec11ed39153df12.png) .
.
Bei geringen Stromstärken können Batterien und Akkumulatoren in guter Näherung als ideale Spannungsquellen angesehen werden.
Netzteile
Für stationäre Anwendungen haben (kabelgebundene) Netzteile mehrere Vorteile gegenüber Batterien oder Akkumulatoren: Sie müssen nicht ausgetauscht werden, und liefern stets zuverlässig (ohne Entladungs-Erscheinungen) die gewünschte Spannung.
Gleichspannungs-Netzteile („DC“ beziehungsweise „Direct Current“) bestehen normalerweise aus einem Transformator, einem (Brücken-)Gleichrichter, einem Spannungsregler und einigen Kondensatoren. Je nach Typ des eingebauten Spannungsreglers liefern Netzteile eine feste oder einstellbare Ausgangs-Spannung.
Spannungsquellen mit Wechselspannung¶
Haushalts-Steckdosen stellen eine Wechselspannung von ![\unit[230]{V}](../_images/math/f45328704ecbfd14e332c696b0fbee26dec78ddf.png) bereit, wobei die zulässige Stromstärke durch Sicherungen meist auf
bereit, wobei die zulässige Stromstärke durch Sicherungen meist auf
![\unit[16]{Ampere}](../_images/math/98ccdafcb22065196d7b4eb8402c577858fc63bd.png) begrenzt ist – es kann somit eine maximale
elektrische Leistung von
begrenzt ist – es kann somit eine maximale
elektrische Leistung von ![\unit[230]{V} \cdot \unit[16]{A} =
\unit[3680]{W}](../_images/math/0682969ba3a2ef3bd01773acb95429ec7dac116b.png) abgegriffen werden. Die elektrische Spannung wird in Kraftwerken
mittels Generatoren (oder mittels Solarzellen und Wechselrichtern) erzeugt und
– nach eine Spannungsanpassung – über (Hoch-)Spannungsleitungen an die
jeweiligen Orte übertragen.
abgegriffen werden. Die elektrische Spannung wird in Kraftwerken
mittels Generatoren (oder mittels Solarzellen und Wechselrichtern) erzeugt und
– nach eine Spannungsanpassung – über (Hoch-)Spannungsleitungen an die
jeweiligen Orte übertragen.
Während elektrische Experimente mit „Netzspannung“ aufgrund der hohen
elektrischen Leistung lebensgefährlich (!!) sind, kann die Wechselspannung des
Stromnetzes ![(\unit[230]{V})](../_images/math/5440f3d6745fe3f63d670d60d0fc738722515e7a.png) mittels eines Transformators einfach auf
eine geringere Spannung eingestellt werden. Je nach Bauweise können sich
Transformatoren entweder direkt in den Geräten befinden (beispielsweise in
Fernsehgeräten, Radios usw.), oder in Form von separaten Netzteilen vorliegen
(beispielsweise bei Notebooks).
mittels eines Transformators einfach auf
eine geringere Spannung eingestellt werden. Je nach Bauweise können sich
Transformatoren entweder direkt in den Geräten befinden (beispielsweise in
Fernsehgeräten, Radios usw.), oder in Form von separaten Netzteilen vorliegen
(beispielsweise bei Notebooks).
Auch für Elektronik-Versuche mit Wechselspannung sollte stets ein geeignetes Wechselspannungs-Netzteil („AC“ beziehungsweise „Alternating Current“) verwendet werden.
Stromquellen¶
So wie eine ideale Spannungsquelle stets die gleiche Nenn-Spannung liefert, liefert eine ideale Stromquelle stets einen gleichen Nenn-Strom; die dafür benötigte Spannung wird von der Stromquelle automatisch geregelt. Wie sich erahnen lässt, lassen sich in der Praxis reale Stromquellen nur schwerer verwirklichen als Spannungsquellen.
Manche Labor-Netzteile können innerhalb bestimmter Grenzen wahlweise als Strom-
oder Spannungsquelle genutzt werden; verwendet man den Stromquellen-Modus, so
lässt sich zudem der gewünschte Nenn-Strom einstellen, beispielsweise
![\unit[1]{A}](../_images/math/e31f7024a861403165d1ded6dfdcadbb394cd035.png) . Stellt die Stromquelle dann fest, dass sie aktuell nur
. Stellt die Stromquelle dann fest, dass sie aktuell nur
![\unit[50]{mA}](../_images/math/bc90ee853a4ad5ac2b1c74658da19173ca899a98.png) abgibt, so erhöht sie intern immer weiter ihre Spannung,
solange bis sich die gewünschte Stromstärke einstellt oder technische Grenzen
erreicht sind.
abgibt, so erhöht sie intern immer weiter ihre Spannung,
solange bis sich die gewünschte Stromstärke einstellt oder technische Grenzen
erreicht sind.
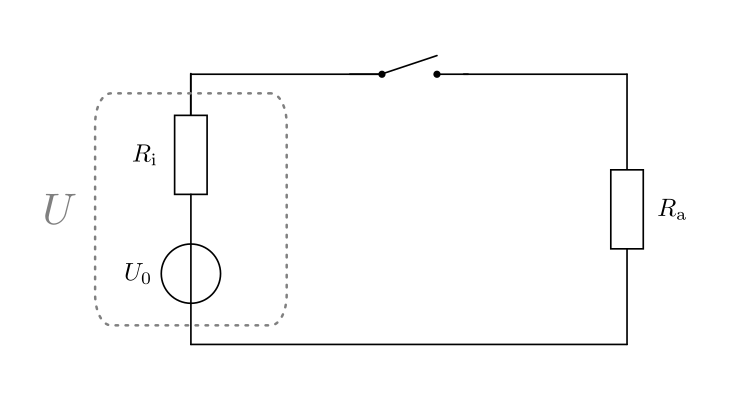
Exkurs 1: Innenwiderstand realer Spannungsquellen¶
Wird ein Stromkreis geschlossen, so muss der Strom – unabhängig von der Art der
Spannungsquelle – stets auch durch diese selbst hindurch fließen. Reale
Spannungsquellen haben hierbei einen eigenen elektrischen Widerstand, den man
„Innenwiderstand“ 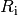 nennt – in Unterscheidung zu den
angeschlossenen Verbrauchern, die man unter dem Begriff „Außenwiderstand“
nennt – in Unterscheidung zu den
angeschlossenen Verbrauchern, die man unter dem Begriff „Außenwiderstand“
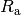 (beziehungsweise „Lastwiderstand
(beziehungsweise „Lastwiderstand 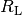 )
zusammenfasst.
)
zusammenfasst.
Der Gesamtwiderstand 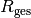 eines Stromkreises ist gleich der
Summe aus dem Innenwiderstand der Spannungsquelle und dem Außenwiderstand:
eines Stromkreises ist gleich der
Summe aus dem Innenwiderstand der Spannungsquelle und dem Außenwiderstand:
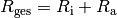
Wie bei einer Reihenschaltung von Widerständen üblich, fällt ein Teil der Gesamtspannung am Innenwiderstand und
der restliche Teil am Außenwiderstand ab. Welcher Anteil der Gesamtspannung am
Außenwiderstand abfällt, hängt vom Anteil 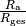 des Außenwiderstands am Gesamtwiderstand ab.[2] Üblicherweise ist der
Außenwiderstand wesentlich größer als der Innenwiderstand, und somit der Anteil
des Außenwiderstands am Gesamtwiderstand nahezu
des Außenwiderstands am Gesamtwiderstand ab.[2] Üblicherweise ist der
Außenwiderstand wesentlich größer als der Innenwiderstand, und somit der Anteil
des Außenwiderstands am Gesamtwiderstand nahezu 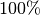 ; folglich fallen
auch fast
; folglich fallen
auch fast 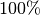 der Gesamtspannung am Außenwiderstand ab.
der Gesamtspannung am Außenwiderstand ab.
Klemmenspannung und Leerlaufspannung
Als „Klemmenspannung“ 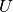 einer Spannungsquelle bezeichnet man diejenige
Spannung, die zwischen den beiden Klemmen (Anschlüssen, Polen) der Spannungsquelle
anliegt; diese Spannung ist mit der Spannung identisch, die über dem
Außenwiderstand des Stromkreises abfällt.
einer Spannungsquelle bezeichnet man diejenige
Spannung, die zwischen den beiden Klemmen (Anschlüssen, Polen) der Spannungsquelle
anliegt; diese Spannung ist mit der Spannung identisch, die über dem
Außenwiderstand des Stromkreises abfällt.
Die Klemmenspannung nimmt ihren maximalen Wert an, wenn der Außenwiderstand
unendlich groß ist: In diesem Fall fällt nahezu die gesamte Spannung am
Außenwiderstand und fast keine Spannung am Innenwiderstand ab. Da bei einem
unendlich großen Außenwiderstand allerdings auch kein Strom fließen kann, wird
dieser maximale Spannungswert auch „Leerlaufspannung“ 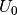 genannt.
genannt.
Die Leerlaufspannung entspricht also dem Spannungswert einer Spannungsquelle, wenn kein Verbraucher angeschlossen ist. Näherungsweise kann dieser Wert mit einem Voltmeter gemessen werden, da dieses zwar keinen unendlichen, aber doch zu einen sehr großen Widerstandswert hat.
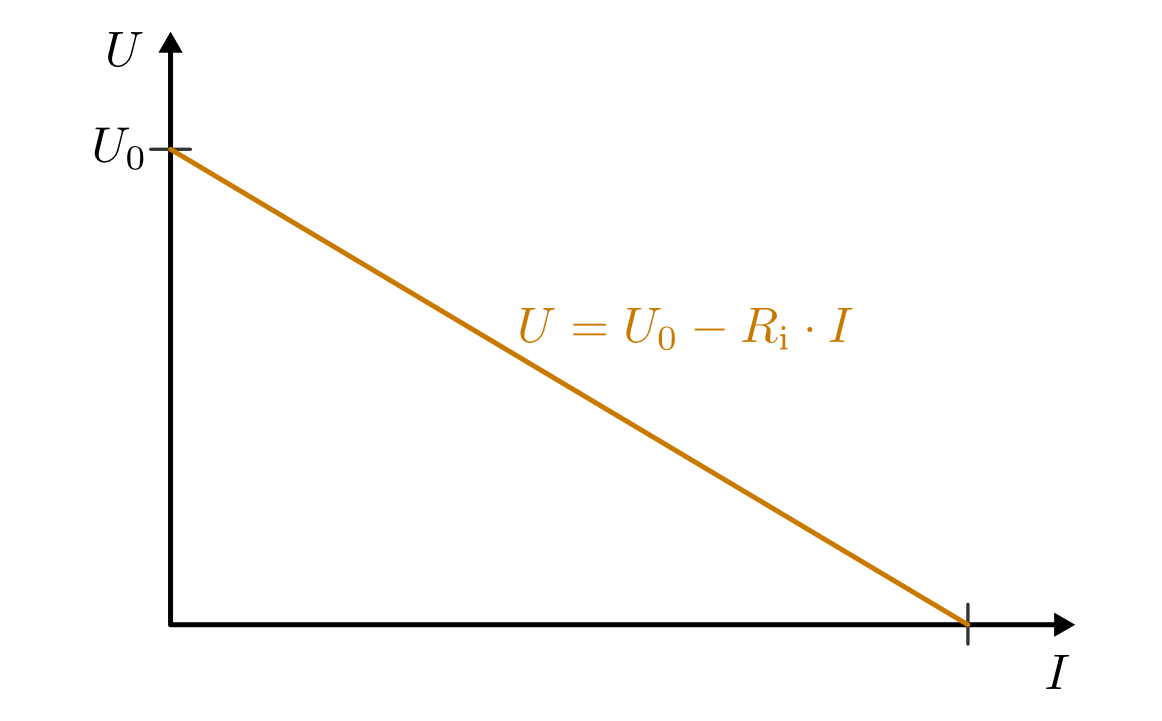
Diagramm der Klemmenspannung einer Spannungsquelle in Abhängigkeit des
Innenwiderstands 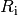 und der fließenden Stromstärke
und der fließenden Stromstärke
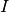 .
.
Wird ein Verbraucher mit einem endlichen Widerstand an die Spannungsquelle
angeschlossen, so stellt sich eine Stromstärke 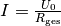 ein, die sowohl durch den Verbraucher wie auch
durch die Spannungsquelle fließt. Am Innenwiderstand
ein, die sowohl durch den Verbraucher wie auch
durch die Spannungsquelle fließt. Am Innenwiderstand 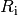 der
Spannungsquelle fällt dabei nach dem Ohmschen Gesetz die
Spannung
der
Spannungsquelle fällt dabei nach dem Ohmschen Gesetz die
Spannung 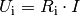 ab; die Klemmenspannung
ist somit um diesen Betrag gegenüber der Leerlaufspannung verringert. Für die
Klemmenspannung
ab; die Klemmenspannung
ist somit um diesen Betrag gegenüber der Leerlaufspannung verringert. Für die
Klemmenspannung 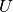 gilt in diesem Fall also:
gilt in diesem Fall also:
(1)¶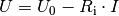
Je niedriger der Außenwiderstand eines Stromkreises ist, desto höher ist die
Stromstärke 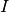 ; dies hat eine Verringerung der Klemmenspannung
; dies hat eine Verringerung der Klemmenspannung 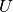 zur Folge.
zur Folge.
Beispiel:
Wie groß ist die Klemmenspannung
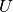 einer Spannungsquelle im Vergleich zu
ihrer Leerlaufspannung
einer Spannungsquelle im Vergleich zu
ihrer Leerlaufspannung 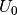 , wenn der Außenwiderstand
, wenn der Außenwiderstand
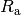 gleich dem Innenwiderstand
gleich dem Innenwiderstand 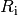 der
Spannungsquelle ist?
der
Spannungsquelle ist?Ist
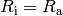 , so folgt für die die Stromstärke
, so folgt für die die Stromstärke
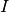 :
: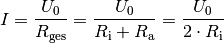
Setzt man diesen Wert in die obige Formel (1) ein, so ergibt sich für die Klemmenspannung
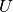 :
: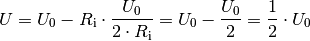
Die Klemmenspannung ist in diesem Fall auf die Hälfte der Leerlaufspannung abgesunken.
Bei einem Kurzschluss sinkt der Außenwiderstand auf nahezu Null ab; die
Stromstärke 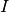 wird dann nur durch den meist sehr niedrigen
Innenwiderstand der Spannungsquelle begrenzt. Die hierbei auftretenden Stromstärken
können so groß sein, dass die Spannungsquelle durch die Wärmewirkung des Stroms
zerstört werden können; bei einem Kurzschluss besteht also Brandgefahr.
wird dann nur durch den meist sehr niedrigen
Innenwiderstand der Spannungsquelle begrenzt. Die hierbei auftretenden Stromstärken
können so groß sein, dass die Spannungsquelle durch die Wärmewirkung des Stroms
zerstört werden können; bei einem Kurzschluss besteht also Brandgefahr.
Batterien und Akkumulatoren können bei einem Kurzschluss ihre gesamte gespeicherte chemische Energie innerhalb von wenigen Minuten abgeben. Die Brandgefahr bei Kurzschlüssen wird in praktischen Anwendungsfällen, beispielsweise in Autos, oftmals durch Feinsicherungen unterbunden: Die darin verbauten Drähte glühen bei zu hohen Stromstärken rasch durch und unterbrechen dadurch den Stromkreis.
Bei Netzteilen muss vom Hersteller eine Belastungsgrenze angegeben werden, die besagt, welche Stromstärke ein Netzteil über längere Zeit liefern kann. Wird die Belastungsgrenze über einen längeren Zeitraum oder kurzzeitig und dafür sehr deutlich überschritten, so können durch Überhitzungen Kurzschlüsse im Netzteil auftreten, die eine Zerstörung des Netzteils sowie ein „Herausfliegen“ der Hauptsicherung im Verteilerkasten (FI-Schalter oder Schmelzsicherung) zur Folge haben kann. In konkreten Anwendungsfällen ist es also ratsam, lieber ein auch für etwas größere Ströme ausgelegtes Netzteil zu verwenden.
Exkurs 2: Innenwiderstand realer Stromquellen¶
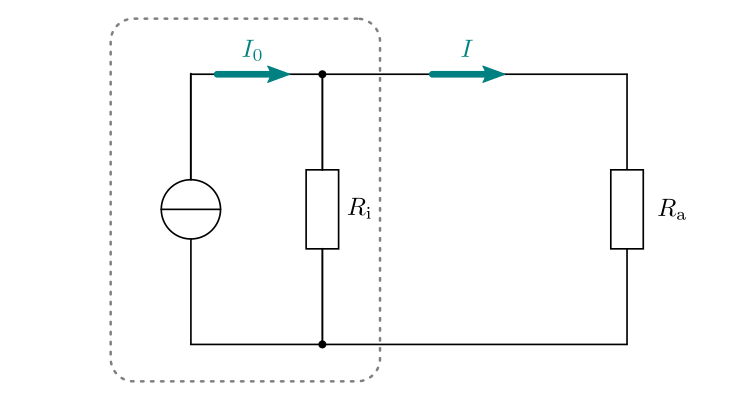
Ein Näherungsmodell mit einer idealen Quelle und einem Innenwiderstand lässt sich auch für reale Stromquellen aufstellen. In diesem Fall sieht das Ersatzschaltbild folgendermaßen aus:
In diesem Fall teilt sich die von der (idealen) Stromquelle ausgehende
Stromstärke auf: Ein Teil fließt über den möglichst hohen Innenwiderstand
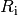 der Stromquelle, ein Teil über den meist vergleichsweise
geringen Last-Widerstand
der Stromquelle, ein Teil über den meist vergleichsweise
geringen Last-Widerstand 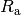 ab. Bezeichnet man mit
ab. Bezeichnet man mit
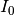 die von der idealen Stromquelle gelieferte Stromstärke und mit
die von der idealen Stromquelle gelieferte Stromstärke und mit
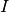 die Stromstärke im restlichen Stromkreis, so gilt:
die Stromstärke im restlichen Stromkreis, so gilt:
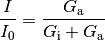
Für die am Lastwiderstand anliegende Spannung 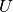 gilt nach dem Ohmschen
Gesetz wiederum:
gilt nach dem Ohmschen
Gesetz wiederum:
(2)¶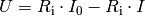
Nimmt man wiederum die durch den Last-Widerstand fließende Stromstärke 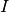 als Variable an, so kann man den nur für das Innere der Stromquelle relevanten
Term
als Variable an, so kann man den nur für das Innere der Stromquelle relevanten
Term 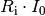 schlichtweg wieder
schlichtweg wieder 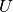 schreiben,
und erhält somit eine Formel, die mit der Gleichung (1)
einer Spannungsquelle identisch ist; bei Verwendung von diesem Modell ist somit
auch die
schreiben,
und erhält somit eine Formel, die mit der Gleichung (1)
einer Spannungsquelle identisch ist; bei Verwendung von diesem Modell ist somit
auch die 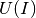 -Kennlinie einer realen Stromquelle mit dem einer realen
Spannungsquelle identisch.
-Kennlinie einer realen Stromquelle mit dem einer realen
Spannungsquelle identisch.
Der wesentliche Unterschied zwischen einer Spannungs- und Stromquelle liegt
darin, auf wie große Außenwiderstände 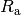 die Quelle
ausgelegt ist:
die Quelle
ausgelegt ist:
- Eine reale Spannungsquelle hat genau dann keine Verlust-Leistung, wenn der
Last-Widerstand
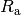 unendlich groß ist. Eine
Spannungsquelle wird somit bevorzugt im Leerlauf beziehungsweise bei geringen
Stromstärken betrieben.
unendlich groß ist. Eine
Spannungsquelle wird somit bevorzugt im Leerlauf beziehungsweise bei geringen
Stromstärken betrieben. - Eine reale Stromquelle hat keine (innere) Verlust-Leistung, wenn der
Außenwiderstand
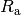 unendlich klein beziehungsweise der
Innenwiderstand
unendlich klein beziehungsweise der
Innenwiderstand 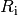 vergleichsweise unendlich groß ist.
vergleichsweise unendlich groß ist.
Der Vorteil der beiden obigen Modelle für Spannungs- und Stromquellen liegt darin, dass sich so dargestellte Quellen auch bei unterschiedlichen Werten parallel beziehungsweise in Reihe schalten lassen, ohne dass sich aus praktische Widersprüche ergeben; die Modelle stellen reale Spannungs- und Stromquellen somit ein gutes Stück realistischer dar.
Anmerkungen:
| [1] | In Deutschland ist jeder Batterien-Händler gesetzlich dazu verpflichtet, entladene Batterien wieder zurück zu nehmen und diese an einer Wertstoff-Sammelstelle abzugeben. |
| [2] | Bei diesem Modell einer Spannungsquelle stellen der Innenwiderstand und und der Last-Widerstand strukturell einen Spannungsteiler dar. |