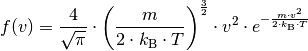Die kinetische Gastheorie¶
Viele reale Gase können unter Standardbedingungen in guter Näherung mittels des Modells der idealen Gase beschrieben werden: Die Anziehungskräfte zwischen den einzelnen Teilchen ist meist vernachlässigbar gering, und ebenso ist das Volumen der einzelnen Teilchen klein im Vergleich zum Gesamtvolumen des Gases. Geht man von diesen Annahmen aus, so kann ein Gas als große Anzahl einzelner Atome oder Moleküle angesehen werden, die sich mit unterschiedlichen Geschwindigkeiten in unterschiedliche Richtungen bewegen, wobei die einzelnen Bewegungsrichtungen und Geschwindigkeiten statistisch gleich verteilt sind.
In einem einfachen Modell kann man von einem einzelnen Gasteilchen ausgehen, das
sich in einem kubischen Behälter in 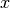 -Richtung auf die linke Wand des
Behälters zu bewegt. Bezeichnet man mit
-Richtung auf die linke Wand des
Behälters zu bewegt. Bezeichnet man mit  die Masse des Gasteilchens und
mit
die Masse des Gasteilchens und
mit 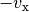 seine ursprüngliche Geschwindigkeit, so gilt für die
Impulsänderung, die das Teilchen bei einem elastischen Stoß mit
der Wand erfährt:
seine ursprüngliche Geschwindigkeit, so gilt für die
Impulsänderung, die das Teilchen bei einem elastischen Stoß mit
der Wand erfährt:
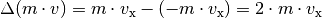
Bis das Teilchen wieder auf die linke Wand trifft, muss es eine Strecke von
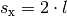 zurücklegen, wenn
zurücklegen, wenn  die Länge des
Würfels ist. Bis zum nächsten Stoß mit der linken Wand vergeht somit folgende
Zeit
die Länge des
Würfels ist. Bis zum nächsten Stoß mit der linken Wand vergeht somit folgende
Zeit 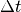 :
:
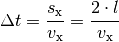
Die Kraft, die das Teilchen auf die Wand ausübt, ist gleich der Impulsänderung je Zeit:
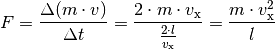
Der Druck, der von dem einzelnen Teilchen auf die linke Wand ausgeübt wird, ist gleich dem Quotienten aus Kraft und Wandfläche:
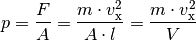
Im letzten Rechenschritt wurde die Beziehung 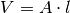 verwendet.
Geht man nun nicht von einem einzelnen, sondern von
verwendet.
Geht man nun nicht von einem einzelnen, sondern von 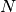 Teilchen aus, die
sich in
Teilchen aus, die
sich in 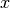 -Richtung mit den Geschwindigkeiten
-Richtung mit den Geschwindigkeiten 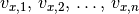 hin- und herbewegen, so addieren sich die
einzelnen Beiträge zum Gesamtdruck:
hin- und herbewegen, so addieren sich die
einzelnen Beiträge zum Gesamtdruck:
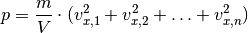
Da in einem Gasvolumen üblicherweise sehr viele Teilchen vorkommen, ist es
wesentlich sinnvoller, anstelle von 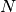 einzelnen
Geschwindigkeits-Quadraten mit
einzelnen
Geschwindigkeits-Quadraten mit 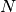 -mal dem mittleren
Geschwindigkeits-Quadrat der Teilchen zu rechnen. Dieses entspricht dem
arithmetischen Mittel der einzelnen Werte:
-mal dem mittleren
Geschwindigkeits-Quadrat der Teilchen zu rechnen. Dieses entspricht dem
arithmetischen Mittel der einzelnen Werte:
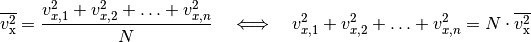
Setzt man diesen Ausdruck in die obige Gleichung ein, so erhält man:
![p &= \frac{m}{V} \cdot N \cdot \overline{v_{\mathrm{x}}^2} \\[4pt]
\Rightarrow p \cdot V &= N \cdot m \cdot \overline{v_{\mathrm{x}}^2} \\[4pt]](../_images/math/ba8c3179f763322d3975c7eb54253d0585091c1f.png)
Bei der Bewegung der Gasteilchen im Behälter tritt keine
Geschwindigkeitsrichtung bevorzugt auf. Wenn sich im Durchschnitt gleich viele
Gasteilchen in 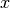 -,
-, 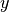 - und
- und  -Richtung bewegen, muss
-Richtung bewegen, muss
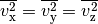 gelten.
gelten.
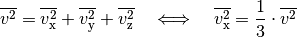
Somit kann die obige Gleichung in folgender Form geschrieben werden:
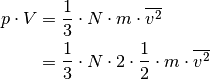
Im letzten Rechenschritt wurde der Term auf der rechten Seite mit 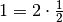 multipliziert, was den Wert des Terms zwar unverändert lässt,
es allerdings ermöglicht, den Faktor
multipliziert, was den Wert des Terms zwar unverändert lässt,
es allerdings ermöglicht, den Faktor 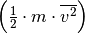 als mittlere kinetische Energie
als mittlere kinetische Energie 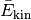 der Gasteilchen aufzufassen. Formt man die Gleichung weiter um, so folgt:
der Gasteilchen aufzufassen. Formt man die Gleichung weiter um, so folgt:
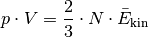
Der Ausdruck 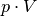 auf der linken Gleichungsseite entspricht nach
der allgemeinen Gasgleichung gerade
auf der linken Gleichungsseite entspricht nach
der allgemeinen Gasgleichung gerade  . Anstelle der allgemeinen Gaskonstante
. Anstelle der allgemeinen Gaskonstante 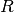 kann auch
kann auch 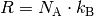 geschrieben werden,
wobei
geschrieben werden,
wobei ![k_{\mathrm{B}} = \unit[1,38 \cdot 10 ^{-23}]{\frac{J}{K}}](../_images/math/7bbd3333c8d0e322a95fee25a3fc3d768297fb01.png) die so
genannte Boltzmann-Konstante
ist.[1] Für
die so
genannte Boltzmann-Konstante
ist.[1] Für ![n=\unit[1]{mol}](../_images/math/8025fd2aa20733bea574f1177f5ad99ab7bc6ba3.png) eines Gases gilt:
eines Gases gilt:
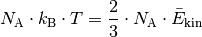
Somit erhält man als Ergebnis der kinetischen Gastheorie schließlich folgende Gleichung:
(1)¶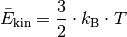
Die kinetische Energie der Gasteilchen nimmt also direkt proportional mit der (absoluten) Temperatur des Gases zu. Mit Hilfe der Gleichung (1) kann einerseits bestimmt werden, welche kinetische Gesamtenergie die Teilchen einer Gasmenge bei einer bestimmten Temperatur aufweisen, andererseits allerdings auch berechnet werden, wie groß die durchschnittliche Geschwindigkeit der einzelnen Gasteilchen bei einer bestimmten Temperatur ist.
Beispiele:
Wie groß ist die kinetische Gesamtenergie aller Moleküle eines idealen Gases bei einer Temperatur von
![\unit[0]{\degree C}](../_images/math/e8140660503109a1fb799efbf73f7c53ebdd405d.png) und einer Stoffmenge von
und einer Stoffmenge von
![n= \unit[1]{mol}](../_images/math/95fd1c4308a104e74c5c00a771b6ba4ec323217a.png) ?
?Nach der kinetischen Gastheorie gilt für die durchschnittliche kinetische Energie eines einzelnen Gasteilchens:
![\bar{E}_{\mathrm{kin}} = \frac{3}{2} \cdot k_{\mathrm{B}} \cdot T =
\frac{3}{2} \cdot \unit[1,38 \cdot 10^{-23}]{\frac{J}{K}} \cdot
\unit[273]{K} \approx \unit[5,65 \cdot 10^{-21}]{J}](../_images/math/7f821293ca63d6582c2668f9143f0f9edd2881e8.png)
Multipliziert man diesen Wert mit der Anzahl
![N_{\mathrm{A}} =
\unit[6,022 \cdot 10 ^{23}]{\frac{1}{mol}}](../_images/math/65c39e041271fb032828e6ab2a6897caaf82c7cf.png) an Teilchen je Mol, so erhält man
als Gesamtenergie für ein Mol an Teilchen:
an Teilchen je Mol, so erhält man
als Gesamtenergie für ein Mol an Teilchen:![\bar{E}_{\mathrm{kin,ges}} = \unit[5,65 \cdot 10^{-21}]{J} \cdot
\unit[6,022 \cdot 10^{23}]{\frac{1}{mol}} \approx
\unit[3403]{\frac{J}{mol}}](../_images/math/3363eba1356e433d8c77ca34c0442afe158170fd.png)
Unter Normalbedingungen nimmt ein Mol eines idealen Gases ein „Normalvolumen“ von
![\unit[22,4]{l}](../_images/math/aecffdb8d53f06fbac584910475b1215c243381b.png) ein. Die
darin enthaltene kinetische Energie
ein. Die
darin enthaltene kinetische Energie ![E_{\mathrm{kin,ges}} \approx
\unit[3,4]{kJ}](../_images/math/95aa78b0e405d513321cfa673cf051f83a1e35a6.png) aller Teilchen entspricht in etwa der kinetischen Energie
eines
aller Teilchen entspricht in etwa der kinetischen Energie
eines ![m=\unit[1]{kg}](../_images/math/1510e0245859c3a750370f70d146364d50ab8b8a.png) schweren Gegenstands, der sich mit einer
Geschwindigkeit von
schweren Gegenstands, der sich mit einer
Geschwindigkeit von ![v=\unit[82,5]{\frac{m}{s}} \approx
\unit[297]{\frac{km}{h}}](../_images/math/ecfebda19b4282f92e0ed72478c1cb9445412664.png) bewegt. Diese beachtliche Energiemenge ist
beispielsweise der Grund dafür, weshalb Wärmepumpen einen Teil der kinetischen
Teilchen-Energien einer kälteren Umgebung „abzapfen“ und einer wärmeren
Umgebung zuführen können.
bewegt. Diese beachtliche Energiemenge ist
beispielsweise der Grund dafür, weshalb Wärmepumpen einen Teil der kinetischen
Teilchen-Energien einer kälteren Umgebung „abzapfen“ und einer wärmeren
Umgebung zuführen können.
Freiheitsgrade mehratomiger Gasteilchen
Nach Gleichung (1) ist die absolute Temperatur ist ein Maß für die mittlere Bewegungsenergie eines Gasteilchens. Ein einatomiges Gas kann sich translatorisch in jede der drei Richtungen des Raumes bewegen; man sagt hierfür, dass ein solches Gasteilchen drei Translations-Freiheitsgrade besitzt. Zusätzlich kann sich ein atomares Gasteilchen um seinen Schwerpunkt drehen (ähnlich wie eine starre Kugel), es besitzt also auch drei Rotations-Freiheitsgrade.
- Einatomige Gase kann man sich modellhaft als „glatte“ Kugeln vorstellen; sie tauschen bei Zusammenstößen keine Rotationsenergie aus. Für einatomige Gase sind somit nur die drei Translations-Freiheitsgrade von Bedeutung.
- Gasteilchen, die aus zwei Atomen bestehen, kann man sich modellhaft wie
„Hanteln“ vorstellen. Man hat experimentell festgestellt, dass bei derartigen
Molekülen unter gewöhnlichen Bedingungen neben den drei
Translations-Freiheitsgraden nur zwei Rotations-Freiheitsgrade in
Erscheinung treten: Das Molekül kann bei normalen Temperaturen um beide
Querachsen rotieren, nicht jedoch um die Längsachse; den dritten
Rotations-Freiheitsgrad bezeichnet man als „eingefroren“.[2] Insgesamt weisen
zweiatomige Gasteilchen somit
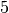 Freiheitsgrade auf.
Freiheitsgrade auf. - Dreiatomige Gase, deren Atome nicht auf einer gemeinsamen Geraden liegen, und mehratomige Gase bezitzen drei (oder sogar mehr) Rotations-Freiheitsgrade.
Für die kinetische Gastheorie sind die Freiheitsgrade der Gasteilchen insofern
von Bedeutung, als dass man festgestellt hat, dass die mittlere kinetische
Energie eines idealen Gases 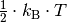 je
Mol und Freiheitsgrad beträgt:
je
Mol und Freiheitsgrad beträgt:
(2)¶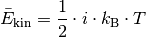
Hierbei ist 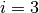 für einatomige Gase,
für einatomige Gase, 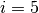 für zweiatomige Gase
und
für zweiatomige Gase
und 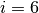 für drei- und mehratomige Gase.
für drei- und mehratomige Gase.
Beispiel:
Wie groß ist die Wurzel aus dem mittleren Geschwindigkeitsquadrat
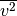 von Luftmolekülen bei
von Luftmolekülen bei ![T = \unit[20]{\degree C}](../_images/math/40929441d76d30a3e41a1b3efaf079c94391cae0.png) ?
?Nach der kinetischen Gastheorie gilt für die durchschnittliche kinetische Energie eines einzelnen Gasteilchens der Masse
 :
: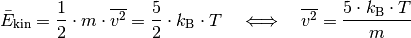
Wie im Abschnitt Teilchenzahl und molare Masse gezeigt, beträgt die Masse von einem Mol an Stickstoff-Teilchen
![\unit[28]{g}](../_images/math/0d32ad4bef39aad7dbebd69da2fb2b68a1e1bdfe.png) , die Masse von einem Mol an Sauerstoff-Teilchen
, die Masse von einem Mol an Sauerstoff-Teilchen
![\unit[32]{g}](../_images/math/3cbcc51ea14c79979dce4538f838f5899329b692.png) . Teilt man diese Werte jeweils durch die Anzahl
. Teilt man diese Werte jeweils durch die Anzahl
![N_{\mathrm{A}} = \unit[6,022 \cdot 10^{23}]{\frac{1}{mol}}](../_images/math/ddd69e9b9409e90c2a04b430c1867f3723bcd243.png) an
Teilchen je Mol, so erhält man als Masse eines Stickstoff- bzw.
Sauerstoff-Teilchens:
an
Teilchen je Mol, so erhält man als Masse eines Stickstoff- bzw.
Sauerstoff-Teilchens:![m_{\ce{N2}} = \frac{\unit[28]{\frac{g}{mol}}}{\unit[6,022 \cdot
10^{-23}]{\frac{1}{mol}}} \approx \unit[4,65 \cdot 10^{-23}]{g} =
\unit[4,65 \cdot 10^{-26}]{kg} \\
m_{\ce{O2}} = \frac{\unit[32]{\frac{g}{mol}}}{\unit[6,022 \cdot
10^{-23}]{\frac{1}{mol}}} \approx \unit[5,31 \cdot 10^{-23}]{g} =
\unit[5,31 \cdot 10^{-26}]{kg}](../_images/math/fa36524efc9b4be90f0cfc5aa66445fc813e75bb.png)
Setzt man diese Werte in die obige Gleichung ein, so erhält man für die Geschwindigkeiten der Stickstoff- und Sauerstoffmoleküle:
![\sqrt{\overline{v^2}_{\ce{N2}}} = \sqrt{\frac{5 \cdot \unit[1,38 \cdot
10^{-23}]{\frac{J}{K}} \cdot \unit[(273+20)]{K}}{\unit[4,6 \cdot
10^{-26}]{kg}}} \approx \unit[663]{\frac{m}{s}} \\
\sqrt{\overline{v^2}_{\ce{O2}}} = \sqrt{\frac{5 \cdot \unit[1,38 \cdot
10^{-23}]{\frac{J}{K}} \cdot \unit[(273+20)]{K}}{\unit[5,3 \cdot
10^{-26}]{kg}}} \approx \unit[618]{\frac{m}{s}} \\](../_images/math/961c059fc94cf84b9eeff2bf2805aeeacfd2e4e8.png)
Die Stickstoffteilchen sind mit rund
![\unit[663]{\frac{m}{s}} \approx
\unit[2340]{\frac{km}{h}}](../_images/math/ca1b85eb1e50ebef440c2bec06a18ab0312917f1.png) somit schneller als die Sauerstoffteilchen mit
rund
somit schneller als die Sauerstoffteilchen mit
rund ![\unit[618]{\frac{m}{s}} \approx \unit[2220]{\frac{km}{h}}](../_images/math/3b4c3e3d83732067a8248b2926583aa8123e8c5a.png) .
.
Je geringer die molare Masse eines Gases ist, desto höher ist bei einer bestimmten Temperatur also die durchschnittliche Geschwindigkeit der enthaltenen Teilchen.
Die Maxwellsche Geschwindigkeitsverteilung
Die Geschwindigkeitswerte der einzelnen Gasteilchen sind statistisch verteilt,
wobei die Verteilung aller vorkommenden Geschwindigkeiten durch eine
Verteilungsfunktion 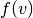 angegeben werden kann. Eine solche Funktion
gibt an, mit welcher Häufigkeit eine Anzahl
angegeben werden kann. Eine solche Funktion
gibt an, mit welcher Häufigkeit eine Anzahl 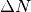 aller
aller 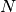 Gasteilchen eine Geschwindigkeit zwischen
Gasteilchen eine Geschwindigkeit zwischen  und
und 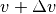 besitzt:[3]
besitzt:[3]
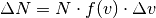
Bei Gasteilchen entspricht die Häufigkeitsverteilung nicht einer Normalverteilung, sondern einer so genannten Maxwellschen Verteilung. Im folgenden Diagramm ist diese Verteilungsfunktion für drei verschiedene Temperaturen dargestellt.
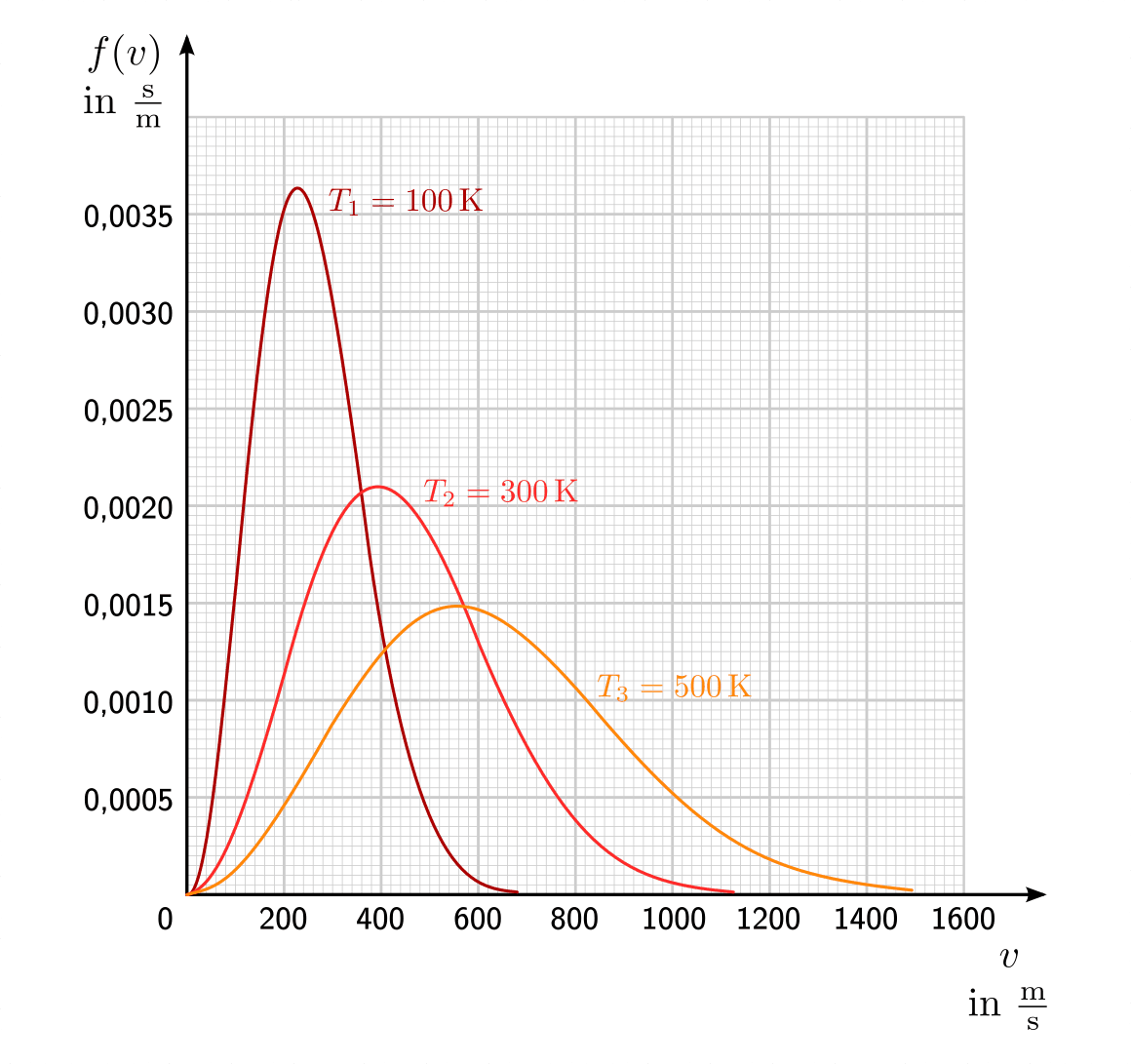
Maxwell-Boltzmann-Verteilung der Geschwindigkeiten von Sauerstoff-Molekülen bei verschiedenen Temperaturen.
Die Geschwindigkeit, die dem Maximum der jeweiligen Kurve entspricht, wird als
wahrscheinlichste Geschwindigkeit 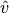 bezeichnet; sie stimmt nicht
mit der mittleren Geschwindigkeit
bezeichnet; sie stimmt nicht
mit der mittleren Geschwindigkeit 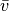 aller Geschwindigkeitswerte
überein.
aller Geschwindigkeitswerte
überein.
… to be continued …
Anmerkungen:
| [1] | Mit ![N_{\mathrm{A}} = \unit[6,022 \cdot 10^{23}]{\frac{1}{mol}}](../_images/math/ddd69e9b9409e90c2a04b430c1867f3723bcd243.png) ist
die sogenannte Avogadro-Konstante gemeint, welche die Anzahl an Teilchen je
mol eines chemischen Stoffes angibt. ist
die sogenannte Avogadro-Konstante gemeint, welche die Anzahl an Teilchen je
mol eines chemischen Stoffes angibt. |
| [2] | Anschaulich kann man sich die Gasteilcchen als „glatte“ Kugeln beziehungsweise Hanteln vorstellen. Durch die glatte Oberfläche können die Teilchen keinen „Spin“ übertragen, ähnlich wie man beim Tischtennis dem Ball keinen Drall mitgeben kann, wenn der Belag des Schlägers glatt und nicht rauh beziehungsweise klebrig ist. Eine Übertragung in Form von Rotationsenergie um die Kugelachse ist somit nicht möglich. |
| [3] | Der Kurvenverlauf der Maxwell-Boltzmann-Verteilung wird über folgende Funktion festgelegt: (3)¶ |