Die Hauptsätze der Wärmelehre¶
Stellt man einen heißen Körper in eine kältere Umgebung, so kühlt er ohne Fremdeinwirkung allmählich ab. Nach einiger Zeit ist er im so genannten thermischen Gleichgewicht mit seiner Umgebung, nimmt also im Normalfall die gleiche Temperatur wie seine Umgebung an.[1] Ebenso werden anfänglich kalte Körper durch eine warme Umgebung bis zum thermischen Gleichgewicht erwärmt.
„Nullter“ Hauptsatz
Steht ein System 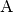 im thermischen Gleichgewicht mit einem
System
im thermischen Gleichgewicht mit einem
System 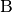 , und steht gleichzeitig das System
, und steht gleichzeitig das System 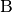 im thermischen Gleichgewicht mit einem weiteren System
im thermischen Gleichgewicht mit einem weiteren System  , so
stehen auch die System
, so
stehen auch die System 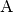 und
und  im thermischen
Gleichgewicht. Diese Feststellung mag trivial klingen, stellt jedoch eine
wichtige Voraussetzung beispielsweise für Temperatur-Messverfahren dar.
im thermischen
Gleichgewicht. Diese Feststellung mag trivial klingen, stellt jedoch eine
wichtige Voraussetzung beispielsweise für Temperatur-Messverfahren dar.
Da historisch gesehen zunächst die anderen drei Hauptsätze formuliert wurden und diese implizit auf die obige Feststellung aufbauen, wurde der genannte Hauptsatz im Nachhinein als „nullter“ Hauptsatz bezeichnet.
Erster Hauptsatz der Wärmelehre¶
Energie kann nicht erzeugt oder vernichtet, sondern nur von einer Energieform
in eine andere umgewandelt werden. Dieser Erhaltungssatz gilt nicht nur für
mechanische Energieformen, sondern auch für Wärmemengen. Wird einem System von
außen eine Wärmemenge 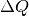 zugeführt oder eine Arbeitsmenge
zugeführt oder eine Arbeitsmenge
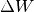 am System verrichtet, so erhöht sich dessen „innere“ Energie
am System verrichtet, so erhöht sich dessen „innere“ Energie
 um genau diesen Betrag:[2]
um genau diesen Betrag:[2]
(1)¶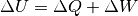
Dieser Zusammenhang, der erstmals von Julius Robert Mayer und Hermann von Helmholtz formuliert wurde, wird
erster Hauptsatz der Wärmelehre genannt. Ist ein System nach außen hin thermisch
isoliert („abgeschlossenes System“), so bleibt die innere Energie  des
Systems erhalten. Wird einem System Arbeit oder Wärme zugeführt, so erhalten die
entsprechenden Mengen in den obigen Gleichungen üblicherweise ein positives,
andernfalls ein negatives Vorzeichen.
des
Systems erhalten. Wird einem System Arbeit oder Wärme zugeführt, so erhalten die
entsprechenden Mengen in den obigen Gleichungen üblicherweise ein positives,
andernfalls ein negatives Vorzeichen.
Beispiele:
Erhitzt man beispielsweise einen Topf mit Wasser auf einer elektrischen Herdplatte, so führt man dem System (Topf) von außen eine Wärmemenge
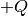 zu. Wird vom Topf weniger Wärme an die Umgebung abgegeben
(beispielsweise durch Wärmestrahlung), so erhöht sich seine innere Energie
und damit seine Temperatur.
zu. Wird vom Topf weniger Wärme an die Umgebung abgegeben
(beispielsweise durch Wärmestrahlung), so erhöht sich seine innere Energie
und damit seine Temperatur.Im umgekehrten Fall gibt jedes System durch Wärmeleitung und/oder Wärmestrahlung eine Wärmemenge
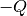 ab,
wenn es in eine kältere Umgebung gebracht wird. In beiden Fällen ändert sich
die innere Energie, ohne dass mechanische Arbeit verrichtet wird.
ab,
wenn es in eine kältere Umgebung gebracht wird. In beiden Fällen ändert sich
die innere Energie, ohne dass mechanische Arbeit verrichtet wird.Reibt man sich die Hände, so erhöht sich deren Temperatur, ohne dass von außen Wärme zugeführt wird. In diesem Fall führt die verrichtete Reibungsarbeit zu einer Erhöhung der inneren Energie.
Im umgekehrten Fall kann sich ein System (beispielsweise ein eingeschlossenes Gas) prinzipiell auch innere Energie abgeben, ohne dass es Wärme mit seiner Umgebung austauscht. Beispielsweise hebt das in einem Verbrennungsmotor bei der Zündung des Luft-Treibstoff-Gemisches entstehende Gas den Hubkolben in kürzester Zeit an; dabei verändert sich sein Druck und sein Volumen. Gegenüber der verrichteten Volumenänderungsarbeit
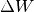 des Gases
ist die durch Wärmeleitung bzw. Wärmestrahlung abgegebene Wärmemenge
des Gases
ist die durch Wärmeleitung bzw. Wärmestrahlung abgegebene Wärmemenge
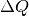 bei diesem Prozess vernachlässigbar klein .
bei diesem Prozess vernachlässigbar klein .
Vorgänge wie im letzten Beispiel, bei denen innere Energie (im Idealfall) ohne Wärmeaustausch in Arbeit umgewandelt wird, nennt man adiabatisch. Sie lassen sich aufgrund stets auftretender Wärmestrahlung und nur endlichen Wärmewiderstandswerten nie vollständig verwirklichen, können aber beispielsweise bei sehr schnell stattfindenden Prozessen zumindest in guter Näherung auftreten.
Der erste Hauptsatz der Wärmelehre schließt als Energie-Erhaltungssatz die Existenz einer Maschine aus, die ohne Zufuhr von Energie mechanische Arbeit verrichten kann.
Wärmequellen, Heiz- und Brennwert
Gibt ein System Wärme an sein Umgebung ab, so wird es als Wärmequelle
bezeichnet. Wird an diesem System keine mechanische Arbeit verrichtet, so stammt
die als Wärme frei werdende Energie aus der chemischen Bindungsenergie der im
System enthaltenen Teilchen; die Abgabe von Wärme geht also mit einer
Verringerung der inneren Energie  des Systems einher.
des Systems einher.
Die Energiemenge, die beim Verbrennen von Heizstoffen wie Holz, Benzin, Diesel,
Kohle oder Erdgas freigesetzt wird, heißt Verbrennungswärme
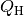 . Sie lässt sich anhand der Masse
. Sie lässt sich anhand der Masse  des
Brennstoffs sowie dessen Heizwert
des
Brennstoffs sowie dessen Heizwert 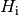 berechnen:
berechnen:
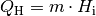
Der Heizwert 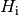 ist eine materialspezifische Größe und wird
bei Festkörpern und Flüssigkeiten üblicherweise in
ist eine materialspezifische Größe und wird
bei Festkörpern und Flüssigkeiten üblicherweise in 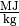 ,
bei Gasen in
,
bei Gasen in 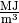 angegeben. Für verschiedene
Materialien ist in Tabellenwerken neben dem Heizwert
angegeben. Für verschiedene
Materialien ist in Tabellenwerken neben dem Heizwert 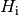 oftmals zusätzlich der Brennwert
oftmals zusätzlich der Brennwert 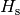 des Materials
angegeben. Letzterer gibt an, wie viel Wärme genutzt werden kann, wenn auch die
Verdampfungswärme des im Brennstoff enthaltenen oder
bei der Verbrennung entstehenden Wasseranteils mit genutzt werden kann.[3]
Hierfür muss der bei der Verbrennung frei werdende Wasserdampf wieder an einer
geeigneten Stelle kondensieren, was bei Öfen oder Verbrennungsmotoren nur in
geringem Umfang möglich ist. Bei der Verbrennung von Nahrungsmitteln in den
einzelnen Körperzellen eines Organismus hingegen wird auch dieser Wärmeanteil
genutzt, so dass der Energiegehalt von Nahrungsmitteln üblicherweise als
Brennwert (ebenfalls in
des Materials
angegeben. Letzterer gibt an, wie viel Wärme genutzt werden kann, wenn auch die
Verdampfungswärme des im Brennstoff enthaltenen oder
bei der Verbrennung entstehenden Wasseranteils mit genutzt werden kann.[3]
Hierfür muss der bei der Verbrennung frei werdende Wasserdampf wieder an einer
geeigneten Stelle kondensieren, was bei Öfen oder Verbrennungsmotoren nur in
geringem Umfang möglich ist. Bei der Verbrennung von Nahrungsmitteln in den
einzelnen Körperzellen eines Organismus hingegen wird auch dieser Wärmeanteil
genutzt, so dass der Energiegehalt von Nahrungsmitteln üblicherweise als
Brennwert (ebenfalls in 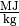 ) angegeben wird.
) angegeben wird.
| Feste und flüssige Brennstoffe | Durchschnittlicher Heizwert in ![\unit[]{MJ/kg}](../_images/math/d9070e334391325822e1834377915b1e8f5d7665.png) |
Gasförmige Brennstoffe | Durchschnittlicher Heizwert in ![\unit[]{MJ/m^3}](../_images/math/3b4514a7137f2efb7a8278c22748090c3075ad38.png) |
| Benzin | 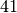 |
Ammoniak | 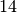 |
| Braunkohle | 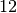 |
Butan | 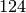 |
| Diesel | 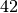 |
Methan | 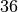 |
| Ethanol | 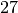 |
Propan | 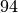 |
| Heizöl | 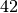 |
Stadtgas | 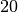 |
| Holz | 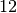 |
Wasserstoff | 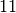 |
| Petroleum | 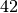 |
||
| Steinkohle | 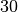 |
Da es sich bei vielen Brennstoffen um Substanzen aus dem Bereich der organischen
Chemie und/oder um Substanzen mit unterschiedlich möglichen Zusammensetzungen
handelt, können die tatsächlichen Heizwerte von den angegebenen
Durchschnittswerten geringfügig abweichen. Bei Nahrungsmitteln wird der
Brennwert aus den Anteilen der drei Energieträger berechnet: Kohlenhydrate haben
einen Brennwert von ![\unit[17,2]{\frac{MJ}{kg}}](../_images/math/c4b6c860582e1fd52012b6705c46a22c0688b0b9.png) , Proteine ebenso; Fette
haben sogar einen Brennwert von
, Proteine ebenso; Fette
haben sogar einen Brennwert von ![\unit[38,9]{\frac{MJ}{kg}}](../_images/math/7a75b87319b1dfce150bb44e9ee4dd013a355876.png) . Die
Brennwerte von Lebensmitteln sind also ähnlich groß wie die Heizwerte der
übrigen gängigen Brennstoffe.
. Die
Brennwerte von Lebensmitteln sind also ähnlich groß wie die Heizwerte der
übrigen gängigen Brennstoffe.
Zweiter Hauptsatz der Wärmelehre¶
Der zweite Hauptsatz der Wärmelehre ist im Laufe der Geschichte auf drei verschiedene Arten formuliert worden, wobei sich herausgestellt hat, dass all diese verschiedenen Formulierungen gleichwertig sind.
Formulierung nach Clausius¶
Der erste Hauptsatz der Wärmelehre schließt zwar die Existenz einer Maschine
aus, die Arbeit ohne Energiezufuhr verrichten kann. Es wäre mit dem ersten
Hauptsatz jedoch denkbar, dass eine Maschine, deren innere Energie  unverändert bleibt, ausschließlich Wärme in Arbeit umwandelt. Beispielsweise
wäre es nach dem ersten Hauptsatz möglich, dass ein Schiff auf einem Ozean in
der Lage ist mechanische Arbeit zu verrichten alleinig dadurch, dass es dem
Ozean Wärme entzieht.
unverändert bleibt, ausschließlich Wärme in Arbeit umwandelt. Beispielsweise
wäre es nach dem ersten Hauptsatz möglich, dass ein Schiff auf einem Ozean in
der Lage ist mechanische Arbeit zu verrichten alleinig dadurch, dass es dem
Ozean Wärme entzieht.
Der zweite Hauptsatz schließt die Existenz eines solchen „Perpetuum Mobiles“ aus, indem er vorgibt, in welche Richtung eine Übertragung von Wärme stattfindet. Diese Tatsache wurde ursprünglich von Rudolf Clausius formuliert:
„Wärme fließt immer vom wärmeren System in Richtung eines kälteren Systems.“
Möchte man mittels einer Maschine Wärme in mechanische Arbeit umwandeln
(„Wärmekraftmaschine“), so benötigt man zunächst zwei unterschiedlich warme
Systeme, so dass überhaupt ein Wärmestrom auftritt. Bringt man diese beiden
Systeme in Kontakt, so fließt eine Wärmemenge 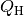 vom heißen
System in Richtung des kälteren. Von diesem Wärmestrom kann ein (zunächst nicht
näher bestimmter) Anteil
vom heißen
System in Richtung des kälteren. Von diesem Wärmestrom kann ein (zunächst nicht
näher bestimmter) Anteil 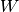 an Arbeit „abgezapft“ werden, die restliche
Wärme
an Arbeit „abgezapft“ werden, die restliche
Wärme 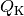 fließt zum kälteren System.
fließt zum kälteren System.
Quantitativ gilt hierbei:
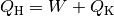
Bei einer Wärmekraftmaschine ist man in erster Linie am Anteil der mechanischen
Arbeit 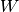 interessiert. Man definiert den Wirkungsgrad
interessiert. Man definiert den Wirkungsgrad 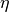 somit als Quotient der verrichteten mechanischen
Arbeit
somit als Quotient der verrichteten mechanischen
Arbeit 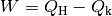 und der dafür investierten
Wärmemenge
und der dafür investierten
Wärmemenge 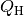 :
:
(2)¶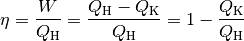
Der so definierte Wirkungsgrad kann nicht größer als 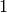 beziehungsweise
beziehungsweise
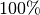 sein; der maximale Wirkungsgrad von
sein; der maximale Wirkungsgrad von 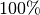 wird genau dann
erreicht, wenn
wird genau dann
erreicht, wenn 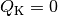 ist, also keine Wärme an das kältere
System fließt.
ist, also keine Wärme an das kältere
System fließt.
Formulierung nach Carnot¶
Bereits in früheren Jahren Sadi Carnot in ähnlicher Weise eine Formel hergeleitet, die den maximalen Wirkungsgrad eine Wärmekraftmaschine beschreibt. Er kam zu folgendem Ergebnis:
(3)¶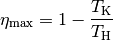
Auch bei dieser Formulierung des zweiten Hauptsatzes kann der Wirkungsgrad einer
Wärmemaschine nicht größer als 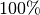 sein; dieser wird genau dann
erreicht, wenn
sein; dieser wird genau dann
erreicht, wenn ![T_{\mathrm{K}} = \unit[0]{K}](../_images/math/f240a890c328df62ede5cf77cf1d224bdff9c9e5.png) ist. Bei jeder anderen
Temperatur ist
ist. Bei jeder anderen
Temperatur ist 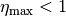 . Der Wirkungsgrad ist umso größer,
desto höher die Temperatur
. Der Wirkungsgrad ist umso größer,
desto höher die Temperatur 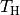 des heißen Systems und desto
niedriger die Temperatur
des heißen Systems und desto
niedriger die Temperatur 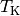 des kalten Systems ist.
des kalten Systems ist.
Carnot hat bei seiner Formulierung zwischen zwei Arten von Prozessen unterschieden:
Reversible Prozesse können in beide Richtungen ablaufen. Die Rückwärtsrichtung entspricht dabei der genauen Umkehrung der Vorwärtsrichtung, als ob eine Videoaufzeichnung rückwärts abgespielt würde. Läuft der Prozess einmal in Hin- und einmal in Rückrichtung ab, so sind beide Systeme anschließend unverändert.
Irreversible Prozesse laufen von selbst nur in eine bestimmte Richtung ab. Um den Prozess in Gegenrichtung ablaufen zu lassen, muss Energie zugeführt werden.
Alle realen Prozesse, in denen Reibung auftritt, sind irreversibel, da die durch Reibungsarbeit erzeugte Wärme nicht wieder zurück in mechanische Arbeit umgewandelt werden kann.
Der maximale Wirkungsgrad 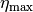 nach Gleichung
(3) gilt exakt für reversible Prozesse, die zwischen zwei
Systemen mit den Temperaturen
nach Gleichung
(3) gilt exakt für reversible Prozesse, die zwischen zwei
Systemen mit den Temperaturen 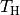 und
und 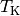 stattfinden („Carnot-Prozess“). Bei irreversiblen Prozessen, also Prozessen mit
Reibung, ist der tatsächliche Wirkungsgrad bei den gegebenen Temperaturen
kleiner als
stattfinden („Carnot-Prozess“). Bei irreversiblen Prozessen, also Prozessen mit
Reibung, ist der tatsächliche Wirkungsgrad bei den gegebenen Temperaturen
kleiner als 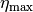 .
.
Kältemaschinen und Wärmepumpen¶
Durch Zuführen von (mechanischer) Arbeit kann ein Prozess entgegen seiner natürlichen Richtung, also vom kalten zum heißen System hin, ablaufen.
Je nach Anwendungszweck unterscheidet man zwischen zwei Prozessarten:
- Bei einer Kältemaschine, beispielsweise einem Kühlschrank oder einer Klimaanlage, wird dem kälteren System mittels mechanischer Arbeit Wärme entzogen, damit dieses weiter abkühlt. Die entzogene Wärme wird an das wärmere System abgegeben.
- Bei einer Wärmepumpe wird dem kalten System mittels mechanischer Arbeit Wärme entzogen, um diese als Nutzwärme einem wärmerem System zuzuführen.
In beiden Anwendungsfällen kann, wie bei einer Wärmekraftmaschine, die
nutzbare Energiemenge in Relation zur aufgewendeten Energiemenge gesetzt werden.
Bei Kältemaschinen und Wärmepumpen kann durch das „Umpumpen“ mehr Wärme
genutzt werden, als mechanische Arbeit investiert werden muss. Anstelle von
einem Wirkungsgrad, der stets kleiner als 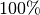 ist, spricht man daher
von so genannten „Leistungszahlen“:
ist, spricht man daher
von so genannten „Leistungszahlen“:
Bei einer Kältemaschine ist die interessierende Größe die Wärmemenge
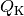 , die dem kalten System entzogen wird. Für die
Leistungszahl
, die dem kalten System entzogen wird. Für die
Leistungszahl  einer Kältemaschine gilt damit:
einer Kältemaschine gilt damit: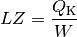
Bei einer Wärmepumpe ist die interessierende Größe die Wärmemenge
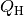 , die dem wärmeren System zugeführt wird. Für die Leistungszahl
, die dem wärmeren System zugeführt wird. Für die Leistungszahl
 einer Wärmepumpe gilt damit:
einer Wärmepumpe gilt damit: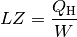
In beiden Fällen sind die Leistungszahlen größer als Eins. Gute Wärmepumpen
können Leistungszahlen von 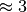 erreichen, bei Kältemaschinen sind
die Leistungszahlen wegen
erreichen, bei Kältemaschinen sind
die Leistungszahlen wegen 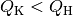 geringer.
geringer.
Entropie¶
Neben den oben beschriebenen Formulierungen von Clausius und Carnot gibt es eine dritte Möglichkeit, den zweiten Hauptsatz der Wärmelehre zu beschreiben; eine zentrale Bedeutung hat hierbei der Begriff der „Entropie“.
Als „Entropie“ 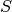 bezeichnet man den „Grad der Unordnung“ eines
thermodynamischen Systems. Der zweite Hauptsatz der Wärmelehre schließt hierbei
aus, dass bei spontan (also ohne Energiezufuhr) ablaufenden Prozessen aus
Unordnung plötzlich Ordnung entsteht. Ein Schreibtisch räumt sich beispielsweise
auch nicht von selbst auf, sondern wird im Lauf der Zeit immer chaotischer, bis
man selbst mal wieder Arbeit verrichtet und Ordnung herstellt; ebenso entstehen
bei einem herunterfallenden Glas von selbst viele chaotisch verteilte
Glasscherben, aber beim Herunterfallen von Glasscherben wird sich nicht von
selbst wieder ein Glasgefäß bilden.
bezeichnet man den „Grad der Unordnung“ eines
thermodynamischen Systems. Der zweite Hauptsatz der Wärmelehre schließt hierbei
aus, dass bei spontan (also ohne Energiezufuhr) ablaufenden Prozessen aus
Unordnung plötzlich Ordnung entsteht. Ein Schreibtisch räumt sich beispielsweise
auch nicht von selbst auf, sondern wird im Lauf der Zeit immer chaotischer, bis
man selbst mal wieder Arbeit verrichtet und Ordnung herstellt; ebenso entstehen
bei einem herunterfallenden Glas von selbst viele chaotisch verteilte
Glasscherben, aber beim Herunterfallen von Glasscherben wird sich nicht von
selbst wieder ein Glasgefäß bilden.
Auf mikroskopischer Ebene kann man sich mechanische Arbeit als gezielte Verschiebung von Teilchen im Raum vorstellen – Wärme hingegen stellt eine ungerichtete Bewegung von Teilchen dar. Es ist möglich eine gerichtete Bewegung in eine ungerichtete umzuwandeln (Arbeit -> Wärme), doch es ohne ein Verrichten von Arbeit nicht möglich, eine ungerichtete Bewegung vieler Teilchen eine vollständig gerichtete Bewegung zu erzeugen. Man sagt daher, dass bei einer Umwandlung von mechanischer Energie in Wärme-Energie diese „entwertet“ wird.
Ähnlich wie bei der potentiellen Energie ist es auch bei der Entropie 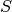 nicht einfach, einen konkreten Wert anzugeben; es ist allerdings möglich, die
Änderung
nicht einfach, einen konkreten Wert anzugeben; es ist allerdings möglich, die
Änderung 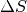 der Entropie bei einem Prozess quantitativ
anzugeben:
der Entropie bei einem Prozess quantitativ
anzugeben:
(4)¶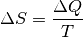
In dieser Formel beschreibt 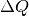 die während des Prozesses
umgesetzte Wärmemenge:
die während des Prozesses
umgesetzte Wärmemenge:
- Ist
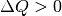 , so wird dem System Wärme zugeführt (wodurch auch die
Entropie zunimmt).
, so wird dem System Wärme zugeführt (wodurch auch die
Entropie zunimmt). - Ist
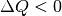 , so wird Wärme vom System abgegeben (wodurch sich
auch die Entropie wieder verringert).
, so wird Wärme vom System abgegeben (wodurch sich
auch die Entropie wieder verringert).
Mit 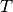 wird die absolute Temperatur bezeichnet, bei welcher der Prozess
abläuft. Ändert sich die Temperatur während eines Prozesses, so kann man
näherungsweise mit der durchschnittlichen Temperatur (in Kelvin) rechnen.[4]
wird die absolute Temperatur bezeichnet, bei welcher der Prozess
abläuft. Ändert sich die Temperatur während eines Prozesses, so kann man
näherungsweise mit der durchschnittlichen Temperatur (in Kelvin) rechnen.[4]
Reversible und nicht reversible Prozesse
Ist die Entropie-Änderung während eines Prozesses gleich Null, so bezeichnet man diesen als „reversibel“: Er kann spontan in beide Richtungen ablaufen. Ein Beispiel für einen solchen Prozess ist das Schmelzen beziehungsweise Gefrieren von Eis:
Beispiel:
Welche Entropie-Änderung ergibt sich insgesamt, wenn
![m=\unit[1,0]{kg}](../_images/math/a7358c329f3fe0d1b217625d3781303a267ef629.png) Eis schmilzt beziehungsweise gefriert?
Eis schmilzt beziehungsweise gefriert?Beim Schmelzen beziehungsweise Gefrieren bleibt die Temperatur konstant; bei einem normalen Luftdruck liegt der Gefrierpunkt von Wasser bei
![T=\unit[0]{\degree C} \approx \unit[273]{K}](../_images/math/e46b81bd799fb7175ff3ac2d6e351dc21c02cc16.png) . Für die zum Schmelzen
des Eises benötigte Schmelzwärme
. Für die zum Schmelzen
des Eises benötigte Schmelzwärme 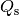 gilt:
gilt:![Q_{\mathrm{s}} = m \cdot q_{\mathrm{s}} = \unit[1,0]{kg} \cdot
\unit[334]{\frac{kJ}{kg}} = \unit[334]{kJ}](../_images/math/d0b277d13cd44eea8da86eba62d7259f89cb9497.png)
Für die Entropieänderung
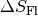 des Wassers ergibt
sich somit:
des Wassers ergibt
sich somit:![\Delta S_{\mathrm{Wasser}} = \frac{\Delta Q}{T} =
\frac{\unit[334]{kJ}}{\unit[273]{K}} \approx \unit[1,22]{\frac{kJ}{K}}](../_images/math/cbdb7cb0b4d31db33ac04b07e70b95246ba163a4.png)
Im gleichen Maß, wie die Entropie des Wassers zunimmt, nimmt die Entropie der Umgebung, welcher die Wärme entzogen wurde, ab:
![\Delta S_{\mathrm{Umgebung}} = \frac{\Delta Q}{T} =
\frac{\unit[-334]{kJ}}{\unit[273]{K}} \approx \unit[-1,22]{\frac{kJ}{K}}](../_images/math/a9775c0c83fcd76373c0fd0e141cdd13a071dc85.png)
Beide Wärme-Umsätze finden bei der gleichen Temperatur statt; da auch die umgesetzten Wärmemengen
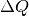 gleich sind, ist die
Gesamt-Entropie-Änderung des gesamten Systems (Wasser + Umgebung) bei beiden
Vorgängen gleich Null:
gleich sind, ist die
Gesamt-Entropie-Änderung des gesamten Systems (Wasser + Umgebung) bei beiden
Vorgängen gleich Null:![\Delta S_{\mathrm{ges}} = \Delta S_{\mathrm{Wasser}} + \Delta
S_{\mathrm{Umgebung}} = \unit[1,22]{\frac{kJ}{kg}} -
\unit[1,22]{\frac{kJ}{kg}} = 0](../_images/math/6b9ade33aec8c2c0e4cb816ae997c4acb9f78c65.png)
Der Vorgang ist somit reversibel – er kann spontan in beide Richtungen ablaufen. Beim Gefrieren ist der Vorgang genau umgekehrt: Das Wasser gibt die Schmelzwärme an die Umgebung ab, wodurch sich die Entropie des Wassers verringert und die Entropie der Umgebung zunimmt; auch hier ist die Entropie-Änderung insgesamt gleich Null.
Andere Prozesse, bei denen sich die Entropie ändert, heißen irreversibel: Sie finden ohne eine externe Energiezufuhr stets nur in Richtung zunehmender Entropie statt.
Welche Entropie-Änderung ergibt sich insgesamt, wenn man in einem isolierten Gefäß
![m_1=\unit[1,0]{kg}](../_images/math/5d13151733aa9f6e223ec1c305c298ab799cb405.png) Wasser mit einer Temperatur von
Wasser mit einer Temperatur von ![T_1 =
\unit[10]{\degree C}](../_images/math/e2914534a0f9f65f7483d52aced10cfb764745b9.png) mit
mit ![m_2=\unit[1,0]{kg}](../_images/math/f4872f776cac9cbcd2599654a23614618e935acf.png) Wasser mit einer
Temperatur von
Wasser mit einer
Temperatur von ![T_2=\unit[30]{\degree C}](../_images/math/96d380353292d50c7946d1ae7d3c87bcd354b63d.png) vermischt?
vermischt?Da die beiden zu vermischenden Flüssigkeiten die gleiche Masse und die gleiche Wärmekapazität
![(c_{\mathrm{wasser}} = \unit[4,2]{\frac{kJ}{kg \cdot
K}})](../_images/math/46dc4322f3fc649d80af7671a309933ccf2135c7.png) haben, wird sich als Mischtemperatur der Mittelwert zwischen beiden
Ausgangs-Temperaturen einstellen, es muss also
haben, wird sich als Mischtemperatur der Mittelwert zwischen beiden
Ausgangs-Temperaturen einstellen, es muss also ![T_{\mathrm{M}} =
\unit[20]{\degree C}](../_images/math/6e8d4f6d3e86bbcc38993da84af735a306c580d7.png) sein.
sein.Geht keine Wärme an die Umgebung verloren, so stammt die zur Erwärmung des kalten Wassers nötige Wärmemenge
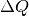 von der warmen Flüssigkeit.
Mit
von der warmen Flüssigkeit.
Mit ![| \Delta T| = \unit[10]{K}](../_images/math/3f4ddd2dc8379e0542a080db6a9ac49ea69a3ac2.png) für beide Flüssigkeiten gilt also:
für beide Flüssigkeiten gilt also:![|\Delta Q_1| = |\Delta Q_2| = m \cdot c \cdot |\Delta T| = \unit[1,0]{kg}
\cdot \unit[10]{K} \cdot \unit[4,2]{\frac{kJ}{kg \cdot K}} = \unit[42]{kJ}](../_images/math/495bea056b3b662f93f802b7815fd49720d4a018.png)
Die aufgegebene beziehungsweise abgegebene Wärmemenge ist betraglich gleich; allerdings ist
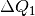 positiv, da dieses System Wärme aufnimmt,
und
positiv, da dieses System Wärme aufnimmt,
und 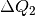 negativ, da dieses System Wärme abgibt. Beide
Teilprozessen (Erwärmen beziehungsweise Abkühlen) finden allerdings bei
unterschiedlichen Durchschnitts-Temperaturen statt: Für die sich erwärmende
Flüssigkeit gilt:
negativ, da dieses System Wärme abgibt. Beide
Teilprozessen (Erwärmen beziehungsweise Abkühlen) finden allerdings bei
unterschiedlichen Durchschnitts-Temperaturen statt: Für die sich erwärmende
Flüssigkeit gilt:![\bar{T}_1 = \frac{T_{\mathrm{1,start}} + T_{\mathrm{1,end}}}{2} =
\unit[\frac{10 + 20}{2}]{\degree C} = \unit[15]{\degree C}](../_images/math/e77231be93fdd6f9b9be031c642345e8f4d23c19.png)
Für die sich abkühlende Flüssigkeit gilt entsprechend:
![\bar{T}_2 = \frac{T_{\mathrm{2,start}} + T_{\mathrm{2,end}}}{2} =
\unit[\frac{30 + 20}{2}]{\degree C} = \unit[25]{\degree C}](../_images/math/9379e649c6078d72e8cf0009d6ef4ba81ce731d9.png)
Die gesamte Entropie-Änderung
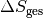 entspricht der
Summe der Entropie-Änderungen beider Teil-Systeme:
entspricht der
Summe der Entropie-Änderungen beider Teil-Systeme:![\Delta S_{\mathrm{ges}} &= \Delta S_1 + \Delta S_2 \\[4pt]
&= \frac{\Delta Q_1}{\bar{T}_1} + \frac{\Delta Q_2}{\bar{T}_2} \\[4pt]
&= \frac{\unit[42]{kJ}}{\unit[(273+15)]{K}} +
\frac{\unit[-42]{kJ}}{\unit[(273+25)]{K}} \\[6pt]
&= \;\;\, \unit[0,1458]{\frac{kJ}{K}} \;\; - \;\; \unit[0,1409]{\frac{kJ}{K}} =
\unit[+4,894]{\frac{J}{K}}](../_images/math/37796bd1b1d20543408d41f08f2fa11d06af13fa.png)
Die Entropie des kälteren Teil-Systems nimmt stärker zu, als die des wärmeren Teil-Systems abnimmt. Die gesamte Entropie-Änderung ist folglich positiv, was auf einen irreversiblen Vorgang schließen lässt: Die vermischten Flüssigkeiten werden sich also nicht wiederum spontan (also ohne Aufwenden von Arbeit) in zwei unterschiedlich warme Teil-Flüssigkeiten aufteilen.
Wie diese beiden Beispiele zeigen, erhöht sich durch Wärmezufuhr nicht zwingend
die Temperatur, stets aber wegen 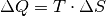 die
Entropie des erwärmten Systems.
die
Entropie des erwärmten Systems.
Dritter Hauptsatz der Wärmelehre¶
Der dritte Hauptsatz der Wärmelehre, auch Nernst’sches Wärmetheorem genannt,
macht eine Aussage über das Verhalten von Stoffen in unmittelbarer Nähe des
absoluten Nullpunktes, also von ![\unit[0]{K}](../_images/math/fa645a285d143fde6652603f2ace81dfe574c8d2.png) . Man kann diesen Hauptsatz
in Kurzform folgendermaßen formulieren:
. Man kann diesen Hauptsatz
in Kurzform folgendermaßen formulieren:
„Es ist unmöglich, ein System durch irgendeinen Vorgang auf den absoluten Nullpunkt abzukühlen.“
Durch den dritten Hauptsatz der Wärmelehre wird somit ein Wirkungsgrad einer
Wärmekraftmaschine von 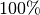 , wie er für einen Carnot-Prozess theoretisch denkbar wäre, explizit ausgeschlossen.
, wie er für einen Carnot-Prozess theoretisch denkbar wäre, explizit ausgeschlossen.
Verwendet man den Begriff der Entropie, so lässt sich der dritte Hauptsatz der Wärmelehre gleichwertig auch folgendermaßen formulieren:
„Am absoluten Nullpunkt ist die Entropie eines Systems gleich Null.“
Anschaulich kann man sich dies etwa so vorstellen: Eine Entropie von Null ist gleichbedeutend mit einer perfekten Ordnung. Um eine solche perfekte Ordnung zu erreichen, muss Arbeit verrichtet beziehungsweise Energie zugeführt werden. Eine Energiezufuhr bewirkt jedoch, dass die Temperatur nicht den absoluten Nullpunkt erreichen kann. Auch mit dieser Formulierung wird somit (implizit) ausgeschlossen, dass der absoulte Temperatur-Nullpunkt erreicht werden kann.
Anmerkungen:
| [1] | Genau genommen hat ein Körper, der im thermischen Gleichgewicht mit seiner Umgebung steht, nur dann die gleiche Temperatur wie die Umgebung, wenn keine Verdunstung auftritt. Dieser Vorgang entzieht dem Körper (beispielsweise einem Glas Wasser) nämlich die zum Verdunsten nötige Wärmemenge, so dass sich eine niedrigere Temperatur als die Umgebungstemperatur einstellt. |
| [2] | Die innere Energie kennzeichnet als Zustandsgröße den energetischen Zustand eines Systems. Sie setzt sich zusammen aus den kinetischen und potentiellen Energien der im System enthaltenen Teilchen sowie den in den einzelnen chemischen Bindungen gespeicherten Bindungsenergien. Während es schwierig ist, den Absolutwert der inneren Energie eines Systems zu bestimmen, können Änderungen der inneren Energie verhältnismäßig leicht gemessen oder berechnet werden. Für die Beschreibung der meisten thermodynamischen Prozesse ist dies bereits ausreichend. |
| [3] | Der Brennwert eines Materials ist stets größer als sein Heizwert. Früher
wurde der Brennwert Auch wenn ein Brennstoff keine Restfeuchte besitzt, kann es bei der Verbrennung zur Bildung von Wasserdampf kommen, wenn einzelne Wasserstoff-Atome des Brennstoffs mit dem Sauerstoff der Luft reagieren. Beim Brennwert wird dann die Wärmemenge mit einbezogen, die diese Menge Wasserdampf beim Kondensieren freisetzt. |
| [4] | Bei einer genaueren Betrachtung muss man den Prozess in kleine Abschnitte
unterteilen und jeweils die einzelnen Wärmeumsätze 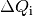 bei der jeweiligen Temperatur bei der jeweiligen Temperatur 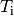 aufsummieren; nutzt man die Integralrechnung ,
so kann man die Entropieänderung während eines Prozesses mittels
aufsummieren; nutzt man die Integralrechnung ,
so kann man die Entropieänderung während eines Prozesses mittels
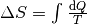 berechnen. berechnen. |



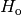 und der Heizwert
und der Heizwert 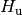 bezeichnet. Inzwischen haben sich allerdings die
entsprechenden lateinischen Bezeichnungen
bezeichnet. Inzwischen haben sich allerdings die
entsprechenden lateinischen Bezeichnungen