Vektoren¶
Darstellung von Vektoren¶
Bei Vektoren handelt es sich aus geometrischer Sicht um Strecken mit einer bestimmten Länge, die sowohl eine bestimmte Richtung, wie auch einen bestimmten Richtungssinn haben; dieser wird in Zeichnungen durch Pfeil am Ende der Strecke hervorgehoben. In der Formelschreibweise werden Vektoren meist mit kleinen lateinischen Buchstaben bezeichnet und durch einen Pfeil über der Vektorgröße markiert.
Je nachdem, ob zwei- oder dreidimensionale geometrische Formen untersucht
werden, reicht ein geordnetes Paar aus zwei oder ein Tupel aus drei
Koordinatenwerten – also 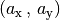 beziehungsweise
beziehungsweise 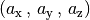 – aus, um einen Vektor
– aus, um einen Vektor  vollständig zu
charakterisieren.[1] Die einzelnen Koordinatenwerte („Komponenten“) geben
dabei an, um wie viele Längeneinheiten die Spitze des Vektors entlang der
jeweiligen Raumrichtung vom Anfangspunkt des Vektors entfernt liegt.
vollständig zu
charakterisieren.[1] Die einzelnen Koordinatenwerte („Komponenten“) geben
dabei an, um wie viele Längeneinheiten die Spitze des Vektors entlang der
jeweiligen Raumrichtung vom Anfangspunkt des Vektors entfernt liegt.
(1)¶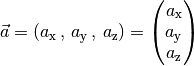
Ein Vektor, dessen Anfangspunkt dem Ursprung des Koordinatensystems
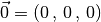 entspricht, wird als Ortsvektor
bezeichnet. Jeder Punkt eines Raumes kann durch einen zugehörigen Ortsvektor
eindeutig charakterisiert werden.
entspricht, wird als Ortsvektor
bezeichnet. Jeder Punkt eines Raumes kann durch einen zugehörigen Ortsvektor
eindeutig charakterisiert werden.
Betrag eines Vektors
Die Länge der Verbindungsstrecke vom Anfangspunkt eines Vektors  zu seinem Endpunkt wird Betrag des Vektors genannt. In Kurzform schreibt man
dafür
zu seinem Endpunkt wird Betrag des Vektors genannt. In Kurzform schreibt man
dafür 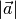 oder
oder  (ohne Vektorpfeil).
(ohne Vektorpfeil).
Der Betrag eines Vektors kann mit Hilfe des Satzes von Pythagoras folgendermaßen
anhand seiner Komponenten 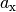 und
und 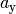 (und
(und
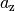 bei dreidimensionalen Vektoren) berechnet werden:
bei dreidimensionalen Vektoren) berechnet werden:
(2)¶![a = | \vec{a } \, | &= \sqrt{a_{\mathrm{x}}^2 + a_{\mathrm{y}}^2}
\phantom{+ a_{\mathrm{z}}^2} \; \quad \text{für zweidimeinsionale
Vektoren} \\[4pt]
a = | \vec{a } \, | &= \sqrt{a_{\mathrm{x}}^2 + a_{\mathrm{y}}^2 +
a_{\mathrm{z}}^2} \quad \text{für dreidimeinsionale Vektoren}](../_images/math/252ad881b8c6a9c527916860f578889e1b289aab.png)
Beispiele:
Der zweidimensionale Vektor
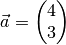 hat folgenden Betrag:
hat folgenden Betrag: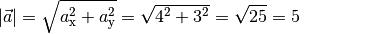
Der dreidimensionale Vektor
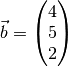 hat folgenden Betrag:
hat folgenden Betrag: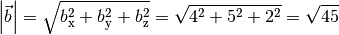
Identische Vektoren
Zwei Vektoren  und
und  sind gleich, wenn sie in allen
Koordinaten übereinstimmen. Beide Vektoren haben dann den gleichen Betrag, die
gleiche Richtung und den gleichen Richtungssinn. Sie können allerdings von
unterschiedlichen Anfangspunkten ausgehen und daher parallel zueinander im Raum
verschoben sein, da für Vektoren stets nur die Differenz der Koordinatenwerte
von Anfangspunkt und Endpunkt von Bedeutung ist.
sind gleich, wenn sie in allen
Koordinaten übereinstimmen. Beide Vektoren haben dann den gleichen Betrag, die
gleiche Richtung und den gleichen Richtungssinn. Sie können allerdings von
unterschiedlichen Anfangspunkten ausgehen und daher parallel zueinander im Raum
verschoben sein, da für Vektoren stets nur die Differenz der Koordinatenwerte
von Anfangspunkt und Endpunkt von Bedeutung ist.
Gegenvektor
Das Negative 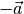 eines Vektors
eines Vektors  , auch „Gegenvektor“
genannt, ist ein Vektor mit gleichem Betrag und gleicher Richtung wie
, auch „Gegenvektor“
genannt, ist ein Vektor mit gleichem Betrag und gleicher Richtung wie
 , jedoch mit umgekehrtem Richtungssinn.
, jedoch mit umgekehrtem Richtungssinn.
In der Komponentenschreibweise kann der zu einem Vektor  gehörende Gegenvektor
gehörende Gegenvektor 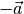 gebildet werden, indem man alle
Komponenten von
gebildet werden, indem man alle
Komponenten von  mit einem Minuszeichen versieht:
mit einem Minuszeichen versieht:
(3)¶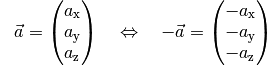
Bei zweidimensionalen Vektoren wird die dritte Komponente 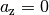 weggelassen.
weggelassen.
Normvektor und Nullvektor
Ein Vektor, dessen Länge genau einer Längeneinheit ![(\unit[1]{LE})](../_images/math/b942846137a7feb84ef1d0b2fd2608e081279efa.png) entspricht, wird „normierter“ Vektor
entspricht, wird „normierter“ Vektor 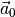 genannt.
genannt.
Ein Vektor mit Betrag Null wird als Nullvektor 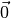 bezeichnet. Bei
einem Nullvektor sind Anfangs- und Endpunkt identisch.
bezeichnet. Bei
einem Nullvektor sind Anfangs- und Endpunkt identisch.
Addition und Subtraktion von Vektoren¶
Ein Vektor kann durch Beibehalten seiner Richtung und seines Richtungssinns, also parallel im Raum verschoben werden, ohne dass sich die Werte seiner Komponenten ändern. Dies kann genutzt werden, um zwei Vektoren zeichnerisch zu addieren beziehungsweise subtrahieren.
Der Summenvektor
Fügt man an einen Vektor  einen zweiten Vektor
einen zweiten Vektor 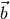 durch eine passende Verschiebung (Translation) so an, dass der Anfangspunkt des
zweiten Vektors mit dem Endpunkt des ersten Vektors übereinstimmt, dann erhält
man den Summenvektor
durch eine passende Verschiebung (Translation) so an, dass der Anfangspunkt des
zweiten Vektors mit dem Endpunkt des ersten Vektors übereinstimmt, dann erhält
man den Summenvektor 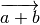 , indem man den Anfangspunkt
des ersten Vektors mit dem Endpunkt des zweiten Vektors verbindet.
, indem man den Anfangspunkt
des ersten Vektors mit dem Endpunkt des zweiten Vektors verbindet.
Rechnerisch erhält man den Summenvektor, indem man die einzelnen Komponenten beider Vektoren addiert:
(4)¶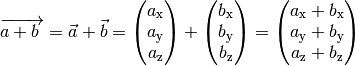
Eine Addition von Vektoren mit unterschiedlicher Dimension ist nicht definiert.
Der Differenzvektor
Die Differenz 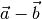 zweier Vektoren lässt sich zeichnerisch
auf ähnliche Weise bestimmen, indem man den Gegenvektor
zweier Vektoren lässt sich zeichnerisch
auf ähnliche Weise bestimmen, indem man den Gegenvektor 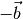 des
zweiten Vektors zum ersten Vektor addiert.
des
zweiten Vektors zum ersten Vektor addiert.
Rechnerisch erhält man den Differenzvektor, indem man die einzelnen Komponenten beider Vektoren subtrahiert:
(5)¶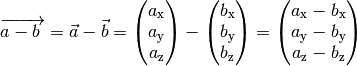
Multiplikation von Vektoren¶
Vektoren können entweder mit einer reellen Zahl (einem so genannten „Skalar“) als auch mit anderen Vektoren multipliziert werden.
Multiplikation eines Vektors mit einer reellen Zahl
Multipliziert man einen Vektor  mit einer reellen Zahl
mit einer reellen Zahl  ,
so ergibt sich ein Vektor, der die gleiche Richtung und den gleichen
Richtungssinn hat, dessen Betrag jedoch um den Faktor
,
so ergibt sich ein Vektor, der die gleiche Richtung und den gleichen
Richtungssinn hat, dessen Betrag jedoch um den Faktor  verändert ist.
verändert ist.
- Ist
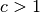 , so wird der Vektor gestreckt.
, so wird der Vektor gestreckt. - Ist
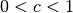 , so wird der Vektor gestaucht.
, so wird der Vektor gestaucht. - Ist
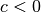 , so wird zusätzlich zur Streckung beziehungsweise Stauchung
des Vektors der Richtungssinn umgedreht.
, so wird zusätzlich zur Streckung beziehungsweise Stauchung
des Vektors der Richtungssinn umgedreht.
Diese Form der Vektor-Multiplikation wird oftmals auch „S-Multiplikation“ genannt.
Rechnerisch lässt sich ein Vektor  mit einer reellen Zahl
mit einer reellen Zahl
 multiplizieren, indem jede Komponente des Vektors mit dieser Zahl
multipliziert wird:
multiplizieren, indem jede Komponente des Vektors mit dieser Zahl
multipliziert wird:
(6)¶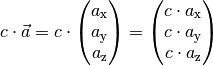
Multipliziert man einen Vektor  mit der Zahl
mit der Zahl 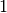 , so bleibt
er unverändert; es gilt also stets:
, so bleibt
er unverändert; es gilt also stets:
(7)¶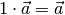
Multipliziert man einen Vektor  hingegen mit dem Kehrwert seines
Betrags
hingegen mit dem Kehrwert seines
Betrags 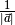 , so erhält man den zugehörigen, auf
eine Längeneinheit
, so erhält man den zugehörigen, auf
eine Längeneinheit ![(\unit[1]{LE})](../_images/math/b942846137a7feb84ef1d0b2fd2608e081279efa.png) normierten Vektor
normierten Vektor 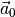 :
:
(8)¶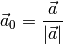
Zusätzlich gelten bezüglich der Multiplikation von Skalaren mit Vektoren das Assoziativ- und Distributivgesetz:
(9)¶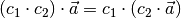
(10)¶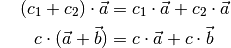
Das Skalarprodukt
Das Skalarprodukt zweier Vektoren  und
und  ist
definiert als das Produkt ihrer Beträge
ist
definiert als das Produkt ihrer Beträge 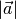 und
und
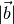 , multipliziert mit dem Cosinus des zwischen ihnen
eingeschlossenen Winkels
, multipliziert mit dem Cosinus des zwischen ihnen
eingeschlossenen Winkels 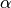 :
:
(11)¶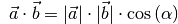
Schreibt man die beiden Vektoren  und
und 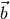 in Spaltenform, so kann das Skalarprodukt komponentenweise nach folgender Formel
berechnet werden:
in Spaltenform, so kann das Skalarprodukt komponentenweise nach folgender Formel
berechnet werden:
(12)¶![{\color{white}\ldots \qquad \qquad \quad }\vec{a} \cdot \vec{b} &=
\begin{pmatrix}
a_{\mathrm{x}} \\
a_{\mathrm{y}} \\
a_{\mathrm{z}} \\
\end{pmatrix} \cdot \begin{pmatrix}
b_{\mathrm{x}} \\
b_{\mathrm{y}} \\
b_{\mathrm{z}} \\
\end{pmatrix} \\[4pt]
&= a_{\mathrm{x}} \cdot b_{\mathrm{x}} + a_{\mathrm{y}} \cdot
b_{\mathrm{y}}+ a_{\mathrm{z}} \cdot b_{\mathrm{z}}](../_images/math/868260edf4e6103ba86da34d3f9d665a40f9037f.png)
Das Ergebnis ist ein skalarer Wert, also eine Zahl. Die Bedeutung des Skalarprodukts wird schnell deutlich, wenn man sich einige Sonderfälle betrachtet:
Stehen die beiden Vektoren
 und
und 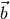 senkrecht
zueinander, so ist
senkrecht
zueinander, so ist 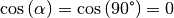 . Somit ergibt
das Skalarprodukt in diesem Fall den Wert Null:
. Somit ergibt
das Skalarprodukt in diesem Fall den Wert Null: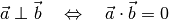
Mit Hilfe dieser Beziehung kann einerseits leicht gepüeft werden, ob zwei Vektoren
 und
und 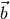 senkrecht aufeinander stehen.
Andererseits kann bei einem Vektor
senkrecht aufeinander stehen.
Andererseits kann bei einem Vektor  mit nur zwei gegebenen
Komponenten unter Verwendung der komponentenweisen Darstellung die dritte
Komponente so bestimmt werden, dass der Vektor auf dem zweiten Vektor
mit nur zwei gegebenen
Komponenten unter Verwendung der komponentenweisen Darstellung die dritte
Komponente so bestimmt werden, dass der Vektor auf dem zweiten Vektor
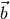 senkrecht steht.
senkrecht steht.Beispiel:
Die dritte Komponente des Vektors
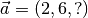 soll so
bestimmt werden, dass er auf dem Vektor
soll so
bestimmt werden, dass er auf dem Vektor 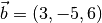 senkrecht steht. Somit muss gelten:
senkrecht steht. Somit muss gelten: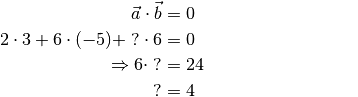
Ist die gesuchte Komponente somit gleich
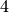 , so stehen beide Vektoren
senkrecht aufeinander.
, so stehen beide Vektoren
senkrecht aufeinander.Stehen die beiden Vektoren
 und
und 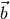 parallel
zueinander, so ist
parallel
zueinander, so ist 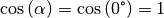 . Das
Skalarprodukt ist in diesem Fall gleich dem Produkt der Beträge beider
Vektoren.
. Das
Skalarprodukt ist in diesem Fall gleich dem Produkt der Beträge beider
Vektoren.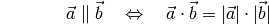
Dieser Zusammenhang wurde implizit bereits verwendet, um den Betrag eines bestimmten Vektors
 zu berechnen. Setzt man nämlich
zu berechnen. Setzt man nämlich
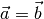 , so gilt:
, so gilt: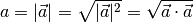
Der Betrag
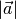 des Vektors kann somit bestimmt werden, indem man
das Skalarprodukt des Vektors mit sich selbst bildet und aus dem Ergebnis die
Quadratwurzel zieht. Schreibt man die obige Gleichung komponentenweise, so
erhält man die übliche Betrags-Gleichung (2).
des Vektors kann somit bestimmt werden, indem man
das Skalarprodukt des Vektors mit sich selbst bildet und aus dem Ergebnis die
Quadratwurzel zieht. Schreibt man die obige Gleichung komponentenweise, so
erhält man die übliche Betrags-Gleichung (2).Für beliebige Winkel
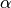 lässt sich das Produkt
lässt sich das Produkt 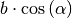 geometrisch als „Projektion“ des Vektors
geometrisch als „Projektion“ des Vektors  auf den
Vektor
auf den
Vektor  deuten. Die Projektion entspricht dabei anschaulich dem
„Schattenwurf“ des Vektors
deuten. Die Projektion entspricht dabei anschaulich dem
„Schattenwurf“ des Vektors 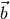 , der sich bei einer senkrecht auf
, der sich bei einer senkrecht auf
 einfallenden Beleuchtung ergeben würde.
einfallenden Beleuchtung ergeben würde.Der Wert des Skalarprodukts ist damit im Allgemeinen gleich dem Betrag des ersten Vektors, multipliziert mit der senkrechten Projektion des zweiten Vektors auf den ersten.
Da das Skalarprodukt komponentenweise einfach zu berechnen ist, kann es auch genutzt werden, um den Winkel zwischen zwei Vektoren oder einem Vektor und einer der Achsen eines (kartesischen) Koordinatensystems zu berechnen. Für den Winkel zwischen zwei Vektoren gilt nämlich aufgrund von Gleichung (11):
![\cos{\left(\alpha\right)} &= \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot
|\vec{b}|} \\[4pt]
\Rightarrow \alpha &= \text{acos}\left(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}|
\cdot |\vec{b}|}\right)](../_images/math/3db97320b906539b1732545cc087d1f9603a7a52.png)
Um den Winkel zu berechnen, muss man somit nur das Skalarprodukt berechnen und dieses durch das Produkt beider Vektor-Beträge dividieren; der Arcus-Cosinus dieses Werts ergibt den gesuchten Winkel.
Um den Winkel zwischen eines Vektors und den einzelnen Raumachsen zu berechnen,
kann man diese ebenfalls durch Vektoren der Länge 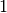 und mit je nur einer
einzigen Vektorkomponente dargestellt werden kann, beispielsweise die
und mit je nur einer
einzigen Vektorkomponente dargestellt werden kann, beispielsweise die
 -Achse durch den Vektor
-Achse durch den Vektor 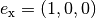 . Man erhält
damit:
. Man erhält
damit:
![{\color{white}\ldots \qquad \quad }\vec{a} \cdot \vec{e}_{\mathrm{x}} &=
\begin{pmatrix}
a_{\mathrm{x}} \\
a_{\mathrm{y}} \\
a_{\mathrm{z}} \\
\end{pmatrix} \cdot \begin{pmatrix}
1 \\
0 \\
0 \\
\end{pmatrix} \\[4pt]
&= a_{\mathrm{x}} \cdot 1 + a_{\mathrm{y}} \cdot 0 + a_{\mathrm{z}} \cdot 0
= a_{\mathrm{x}}](../_images/math/da3e635e90a022a5e76de65b777250cea7d3cfb1.png)
Gleiches gilt auch für die Skalarprodukte von  mit den beiden
anderen Raumachsen. Die allgemeine Formel (11) des
Skalarprodukts kann damit nach dem gesuchten Winkel
mit den beiden
anderen Raumachsen. Die allgemeine Formel (11) des
Skalarprodukts kann damit nach dem gesuchten Winkel 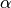 aufgelöst
werden:
aufgelöst
werden:
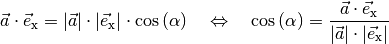
Setzt man 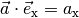 und
und
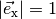 in die obige Gleichung ein, so folgt:[2]
in die obige Gleichung ein, so folgt:[2]
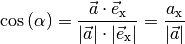
Für die Winkel 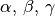 zwischen
zwischen  und
den
und
den 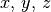 -Achsen gilt somit:
-Achsen gilt somit:
(13)¶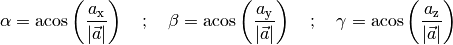
Das Vektorprodukt
Das Vektorprodukt zweier Vektoren  und
und 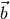 ergibt
einen Vektor, der auf jedem der beiden Vektoren und senkrecht steht. Diese
Definition ist erst ab einem dreidimensionalen Raum sinnvoll.
ergibt
einen Vektor, der auf jedem der beiden Vektoren und senkrecht steht. Diese
Definition ist erst ab einem dreidimensionalen Raum sinnvoll.
Der Betrag des Vektorprodukts zweier Vektoren  und
und
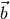 ist gleich dem Produkt ihrer Beträge
ist gleich dem Produkt ihrer Beträge 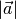 und
und
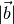 , multipliziert mit dem Sinus des zwischen ihnen
eingeschlossenen Winkels
, multipliziert mit dem Sinus des zwischen ihnen
eingeschlossenen Winkels 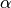 :
:
(14)¶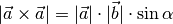
Schreibt man die beiden Vektoren  und
und  in
Spaltenform, so kann das Vektorprodukt komponentenweise nach folgender Formel
berechnet werden:
in
Spaltenform, so kann das Vektorprodukt komponentenweise nach folgender Formel
berechnet werden:
(15)¶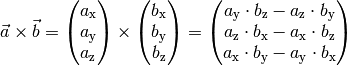
Das Vektorprodukt findet Anwendung in der analytischen Geometrie und in der Technik. Beispielsweise kann zu zwei gegebenen Richtungsvektoren, die eine Ebene beschreiben, mit Hilfe des Vektorprodukts ein dritter „Normvektor“ gefunden werden, der auf der Ebene senkrecht steht. In der Physik wird das Vektorprodukt beispielsweise bei der Berechnung von Drehmomenten und Drehimpulsen genutzt.
Anmerkungen:
| [1] | Vektoreigenschaften lassen sich so verallgemeinern, dass in der
algebraischen Geometrie allgemein auch Vektoren mit  Dimensionen
behandelt werden können. Dimensionen
behandelt werden können. |
| [2] | Der Betrag des Vektors  ist gleich Eins, da ist gleich Eins, da
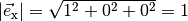 gilt. gilt. |







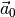 eines Vektors
eines Vektors 
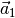 und
und
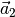 .
.
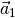 und
und 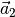 .
.
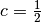 beziehungsweise
beziehungsweise 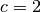 ).
).
