Grundbegriffe¶
Einige geometrische Gebilde treten in der Geometrie besonders häufig und in verschiedenen Zusammenhängen auf. Die wichtigsten dieser Grundelemente und damit zusammenhängende Begriffe werden im folgenden Abschnitt zusammenfassend vorgestellt.
Punkt, Gerade, Strecke und Strahl¶
Punkt und Dimension
Das vielleicht grundlegendste Objekt der Geometrie ist der Punkt. Ein Punkt ist
dimensionslos, besitzt also keine räumliche Ausdehnung. Die Lage eines Punktes
im Raum wird für gewöhnlich durch Koordinaten angegeben, beispielsweise
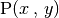 für einen Punkt im zweidimensionalen Raum oder
für einen Punkt im zweidimensionalen Raum oder
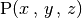 für einen Punkt im dreidimensionalen
Raum. Die Dimension eines Objekts gibt an, wie viele Raumrichtungen zur
Beschreibung seiner geometrischen Eigenschaften berücksichtigt werden müssen.
für einen Punkt im dreidimensionalen
Raum. Die Dimension eines Objekts gibt an, wie viele Raumrichtungen zur
Beschreibung seiner geometrischen Eigenschaften berücksichtigt werden müssen.
Geraden und Halbgeraden
Eine Gerade 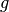 entspricht anschaulich einer Bahn, die sich ergibt, wenn
sich ein Punkt ohne Änderung der Richtung unbegrenzt hin- und herbewegt. Eine
Gerade weist stets eine eindeutige Richtung im Raum auf, hat jedoch im
Allgemeinen keinen „Richtungssinn“, sie besitzt also keinen klar definierten
Anfang als Startpunkt und kein klar definiertes Ende als Zielpunkt.[1]
Vielmehr besteht jede Gerade aus einer Menge von unendlich vielen Punkten, die
sich auf der geradlinigen Bahn befinden.
entspricht anschaulich einer Bahn, die sich ergibt, wenn
sich ein Punkt ohne Änderung der Richtung unbegrenzt hin- und herbewegt. Eine
Gerade weist stets eine eindeutige Richtung im Raum auf, hat jedoch im
Allgemeinen keinen „Richtungssinn“, sie besitzt also keinen klar definierten
Anfang als Startpunkt und kein klar definiertes Ende als Zielpunkt.[1]
Vielmehr besteht jede Gerade aus einer Menge von unendlich vielen Punkten, die
sich auf der geradlinigen Bahn befinden.
Die Richtung einer Geraden wird bereits durch die Angabe zweier auf ihr liegender Punkte eindeutig festgelegt. Da jede Gerade stets nur entlang einer Raumrichtung verläuft, ist ihre Dimension gleich eins.
Betrachtet man einen Punkt  , der auf einer Geraden liegt, so wird
diese durch den Punkt in zwei Halbgeraden unterteilt. Liegt ein weiterer Punkt
, der auf einer Geraden liegt, so wird
diese durch den Punkt in zwei Halbgeraden unterteilt. Liegt ein weiterer Punkt
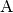 auf der einen, ein Punkt
auf der einen, ein Punkt 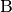 auf der anderen
Halbgeraden, so schreibt man für beide Halbgeraden auch kurz
auf der anderen
Halbgeraden, so schreibt man für beide Halbgeraden auch kurz
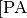 bzw.
bzw. 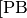 .
.
Als Strahl bezeichnet man eine Halbgerade, der ein eindeutiger Richtungssinn zugewiesen wird.
Eine Strecke 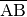 entspricht der Menge aller Punkte,
die sich zwischen zwei auf Punkten
entspricht der Menge aller Punkte,
die sich zwischen zwei auf Punkten 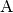 und
und 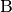 einer
Geraden befinden; diese werden ebenfalls zur Punktmenge hinzugenommen. Eine
Strecke entspricht stets dem kürzesten Abstand zwischen beiden Endpunkten.
einer
Geraden befinden; diese werden ebenfalls zur Punktmenge hinzugenommen. Eine
Strecke entspricht stets dem kürzesten Abstand zwischen beiden Endpunkten.
Als Pfeil (oder Vektor) 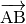 bezeichnet man eine
Strecke zwischen zwei Punkten
bezeichnet man eine
Strecke zwischen zwei Punkten 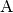 und
und 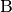 , die einen
eindeutigen Richtungssinn aufweist.
, die einen
eindeutigen Richtungssinn aufweist.
Auf die Darstellung von Strecken, Vektoren und Geraden mittels Koordinaten wird im Abschnitt der Strecken und Geraden näher eingegangen.
Parallelität und Winkel¶
Verlaufen zwei voneinander verschiedene Geraden 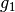 und
und 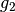 entlang der gleichen Richtung, so heißen sie zueinander parallel.[2] Beide
Geraden haben an jeder Stelle den gleichen Abstand
entlang der gleichen Richtung, so heißen sie zueinander parallel.[2] Beide
Geraden haben an jeder Stelle den gleichen Abstand 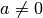 voneinander
und somit keinen gemeinsamen Punkt („Schnittpunkt“).
voneinander
und somit keinen gemeinsamen Punkt („Schnittpunkt“).
Der Abstand eines Punktes zu einer Geraden wird stets senkrecht zu dieser Geraden gemessen; dies entspricht der kürzest möglichen Strecke zwischen diesem Punkt und einem Punkt auf der Geraden. Der Abstand zweier paralleler Geraden entspricht dem Abstand irgendeines Punktes der einen Geraden zur anderen Geraden.
Winkel und Gradmaß
Gehen zwei Strahlen von einem gemeinsamen Punkt 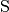 („Scheitel“)
aus, so bezeichnet man den Richtungsunterschied zwischen beiden Strahlen als
Winkel. Üblicherweise werden Winkel mit griechischen Kleinbuchstaben
symbolisiert; beschreibt der Winkel eine Drehung des Strahls gegen den
Uhrzeigersinn, so wird er positiv genannt, andernfalls negativ. Liegen auf den
zwei Strahlen (auch „Winkelschenkel“ genannt) die Punkte
(„Scheitel“)
aus, so bezeichnet man den Richtungsunterschied zwischen beiden Strahlen als
Winkel. Üblicherweise werden Winkel mit griechischen Kleinbuchstaben
symbolisiert; beschreibt der Winkel eine Drehung des Strahls gegen den
Uhrzeigersinn, so wird er positiv genannt, andernfalls negativ. Liegen auf den
zwei Strahlen (auch „Winkelschenkel“ genannt) die Punkte 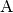 und
und
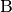 , so schreibt man auch
, so schreibt man auch 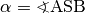 .
.
Die Größe eines Winkels wird üblicherweise in Grad angegeben. Ein Grad
entspricht dabei einem 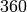 -tel einer vollen Umdrehung; wird also ein
Strahl um einen Winkel von
-tel einer vollen Umdrehung; wird also ein
Strahl um einen Winkel von 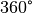 gedreht, so ist er deckungsgleich mit
dem ursprünglichen Strahl. Je nach Winkelgröße unterscheidet man folgende
Winkelarten:
gedreht, so ist er deckungsgleich mit
dem ursprünglichen Strahl. Je nach Winkelgröße unterscheidet man folgende
Winkelarten:
- Gilt
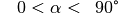 , so nennt man den
Winkel „spitz“.
, so nennt man den
Winkel „spitz“. - Gilt
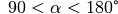 , so nennt man den Winkel
„stumpf“.
, so nennt man den Winkel
„stumpf“. - Gilt
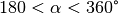 , so nennt man den Winkel „überstumpf“.
, so nennt man den Winkel „überstumpf“.
Gilt für einen Winkel 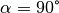 , so wird er als „rechter Winkel“
bezeichnet, bei
, so wird er als „rechter Winkel“
bezeichnet, bei 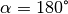 wird ein Winkel „gestreckter Winkel“
genannt. Im Fall
wird ein Winkel „gestreckter Winkel“
genannt. Im Fall 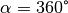 , also einer vollen Umdrehung,
bezeichnet man den Winkel auch als „Vollwinkel“.
, also einer vollen Umdrehung,
bezeichnet man den Winkel auch als „Vollwinkel“.
Für die Angabe von sehr kleinen Winkelgrößen sind auch die Einheiten
„Winkelminute“ und „Winkelsekunde“ gebräuchlich. Ein Grad entspricht 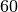 Winkelminuten, eine Winkelminute wiederum
Winkelminuten, eine Winkelminute wiederum 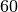 Winkelsekunden. Dabei ist
folgende Schreibweise üblich:
Winkelsekunden. Dabei ist
folgende Schreibweise üblich:
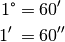
Das Bogenmaß, das ebenfalls häufig für Winkelangaben Verwendung findet, wird im Abschnitt Gradmaß und Bogenmaß näher beschrieben.
Scheitelwinkel und Nebenwinkel
Schneiden sich zwei Geraden, so ergänzen sich zwei nebeneinander liegende
Winkel jeweils zu 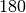 . Für je zwei so genannte „Nebenwinkel“
. Für je zwei so genannte „Nebenwinkel“
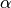 und
und 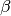 gilt also:
gilt also:
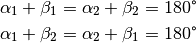
Die einander gegenüberliegenden Winkel zweier sich schneidender Geraden heißen „Scheitelwinkel“. Scheitelwinkel sind paarweise stets gleich groß, es gilt also immer:
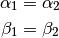
Stufenwinkel und Wechselwinkel
Zeichnet man zu einer von zwei sich schneidenden Geraden eine parallel Gerade, so liegen am zweiten Schnittpunkt identische Winkelverhältnisse vor wie am ersten. Die Winkel, die auf der gleichen Seite der die beiden Parallelen schneidenden Geraden liegen, heißen „Stufenwinkel“ (oder kurz: „F“-Winkel), die einander gegenüber liegenden Winkel „Wechselwinkel“ (oder kurz: „Z“-Winkel).

Stufenwinkel und Wechselwinkel zweier paralleler Geraden 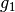 und
und
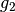 , die von einer weiteren Geraden
, die von einer weiteren Geraden 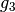 geschnitten werden.
geschnitten werden.
In der Abbildung Stufenwinkel und Wechselwinkel sind beispielsweise 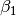 und
und
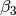 als Stufenwinkel gleich groß, es gilt also
als Stufenwinkel gleich groß, es gilt also 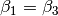 . Ebenso gilt
. Ebenso gilt  , da es sich bei diesen beiden
Winkeln um Wechselwinkel handelt.[3]
, da es sich bei diesen beiden
Winkeln um Wechselwinkel handelt.[3]
Zueinander senkrechte Winkel
Stehen die Strahlen zweier Winkel senkrecht aufeinander, so sind die beiden
Winkel gleich groß. Der Grund dafür ist, dass die beiden aneinander liegenden
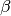 -Winkel Scheitelwinkel darstellen, also gleich groß sind. Da die
Summe der Winkel in einem Dreieck stets
-Winkel Scheitelwinkel darstellen, also gleich groß sind. Da die
Summe der Winkel in einem Dreieck stets 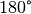 beträgt und in
beiden Dreiecken je ein Winkel gleich
beträgt und in
beiden Dreiecken je ein Winkel gleich 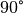 ist, folgt aus der
Gleichheit von
ist, folgt aus der
Gleichheit von 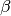 auch die Gleichheit von
auch die Gleichheit von 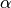 .
.
Eine naturwissenschaftliche Anwendung dieses Zusammenhangs stellt beispielsweise das Kraftverhältnis an einer schiefen Ebene dar.
Anmerkungen:
| [1] | Wird einer Geraden willkürlich ein Richtungssinn zugewiesen, so spricht man von einer „orientierten“ Geraden. |
| [2] | Sind zwei orientierte Geraden 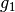 und und 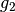 zueinander
parallel, so können sie „gleichsinnig parallel“ (Symbol: zueinander
parallel, so können sie „gleichsinnig parallel“ (Symbol: 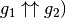 oder „antiparallel“ (Symbol: oder „antiparallel“ (Symbol: 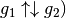 zueinander verlaufen. zueinander verlaufen. |
| [3] | Genau genommen gilt sogar 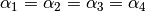 sowie sowie 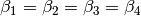 ,
da es sich jeweils paarweise um Stufen- bzw. Wechselwinkel handelt. ,
da es sich jeweils paarweise um Stufen- bzw. Wechselwinkel handelt. |





 zweier paralleler Geraden
zweier paralleler Geraden 


