Ungleichungen¶
Sind zwei Terme  und
und  durch die Kleiner-als-Relation
durch die Kleiner-als-Relation
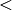 oder die Größer-als-Relation
oder die Größer-als-Relation 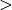 miteinander verbunden, so
spricht man von einer Ungleichung.[1]
miteinander verbunden, so
spricht man von einer Ungleichung.[1]
(1)¶
Für Ungleichungen gilt ebenso wie für Gleichungen, dass man durch Belegung der Variablen mit konkreten Werten eine
wahre oder falsche Aussage erhält. Die Definitionsmenge 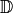 einer
Ungleichung ist, sofern durch die Terme
einer
Ungleichung ist, sofern durch die Terme  und
und  keine
Einschränkung vorgegeben ist, gleich der Menge
keine
Einschränkung vorgegeben ist, gleich der Menge 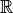 der reellen
Zahlen.
der reellen
Zahlen.
Ungleichungen können keine, eine, mehrere oder unendlich viele Lösungen haben.
Im Allgemeinen besteht die zu bestimmende Lösungsmenge  aus so
genannten Intervallen, also aus Teilbereichen von
aus so
genannten Intervallen, also aus Teilbereichen von 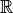 . Jedes
Intervall hat eine untere Grenze
. Jedes
Intervall hat eine untere Grenze  und eine obere Grenze
und eine obere Grenze  und
umfasst somit alle Zahlen
und
umfasst somit alle Zahlen  , die zwischen diesen Grenzen liegen.
, die zwischen diesen Grenzen liegen.
Intervalle lassen sich auf einfache Weise durch eckige Klammern angeben. Je nachdem, ob die Grenzen eines Intervalls noch zum Intervall gehören sollen oder nicht, unterscheidet man folgende Fälle:
- Für ein geschlossenes Intervall gilt
 .Man schreibt dafür
.Man schreibt dafür![[a \,;\, b]](../_images/math/184cb1976d9611db179453388d94002457c5ba1d.png) .
. - Für ein halboffenes Intervall gilt entweder
 oder
oder
 .Man schreibt dafür
.Man schreibt dafür beziehungsweise
beziehungsweise ![]a \,;\, b]](../_images/math/47c5934e54e5b9e9ef6b0b792030e3d463bfda01.png) .
. - Für ein offenes Intervall gilt
 .Man schreibt dafür
.Man schreibt dafür![]a \,;\, b[](../_images/math/c45ba02c4b0dd6ac6e534e4abab8e78e511d76b4.png) .
.
Lösen von Ungleichungen
Ungleichungen lassen sich ebenso wie Gleichungen durch schrittweises Umformen lösen. Auch hierfür spielen äquivalente Umformungen eine wesentliche Rolle. Beispielsweise lassen sich die linke und die rechte Seite einer Ungleichung vertauschen, wenn gleichzeitig auch das Relationszeichen „umgedreht“ wird:

Termumformungen, die sich nur auf eine Seite einer Gleichung auswirken, beispielsweise Zusammenfassen und Ausmultiplizieren beziehungsweise Ausklammern von Summentermen sowie Kürzen und Erweitern von Bruchtermen, dürfen ohne Änderung des Relationszeichens jederzeit vorgenommen werden.
Eine Ungleichung bleibt zudem unverändert, wenn man auf beiden Seiten einen
beliebigen Term  addiert oder subtrahiert.
addiert oder subtrahiert.
![T_1 < T_2 \quad &\Leftrightarrow \quad T_1 + T < T_2 + T \\[2pt]
T_1 < T_2 \quad &\Leftrightarrow \quad T_1 - T < T_2 - T \\[2pt]](../_images/math/319f4d961322a3292ebc218fda3fc9555480b9d3.png)
Multipliziert oder dividiert man eine Gleichung mit beziehungsweise durch einen
Term  , so muss zum einen – wie bei Gleichungen – auf die Bedingung
, so muss zum einen – wie bei Gleichungen – auf die Bedingung
 geachtet werden, da ansonsten zusätzliche Lösungen hinzukommen
beziehungsweise ursprünglich gültige Lösung verschwinden können. Zum anderen ist
zu beachten, dass das Relationszeichen umgedreht werden muss, wenn
geachtet werden, da ansonsten zusätzliche Lösungen hinzukommen
beziehungsweise ursprünglich gültige Lösung verschwinden können. Zum anderen ist
zu beachten, dass das Relationszeichen umgedreht werden muss, wenn  ist. Somit gilt:
ist. Somit gilt:
![T_1 < T_2 \quad &\Leftrightarrow \quad T_1 \, \cdot \; T < T_2 \, \cdot
\; T \qquad (T > 0)\\[2pt]
T_1 < T_2 \quad &\Leftrightarrow \quad T_1 \, : \, T < T_2 \, : \, T
\qquad (T > 0)](../_images/math/259ac4e6397c947d7ae910c4f62582242d3cd7bd.png)
beziehungsweise
![T_1 < T_2 \quad &\Leftrightarrow \quad T_1 \, \cdot \; T > T_2 \, \cdot
\; T \qquad (T < 0)\\[2pt]
T_1 < T_2 \quad &\Leftrightarrow \quad T_1 \, : \, T > T_2 \, : \, T
\qquad (T < 0)](../_images/math/8b3739d17e96d48e0d586912c860c0b95f90ae4b.png)
Werden neben den vier grundlegenden Rechenoperationen (Addition, Subtraktion, Multiplikation und Division) weitere Rechenoperationen (beispielsweise Potenzieren, Wurzelziehen oder Logarithmieren) angewendet, so sind wiederum zusätzliche Überlegungen nötig.
Lineare Ungleichungen¶
Eine Ungleichung heißt linear, wenn sie in folgender allgemeiner Form dargestellt werden kann:
(2)¶
 , falls
, falls
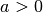 ist. Wenn andernfalls
ist. Wenn andernfalls 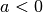 gilt, so ist die Lösung
gilt, so ist die Lösung
 .
.Beispiel:
Für welche
 -Werte gilt die folgende Ungleichung?
-Werte gilt die folgende Ungleichung?
Zunächst wird die Gleichung in die allgemeine Form
 gebracht:
gebracht:
Da in diesem Fall der Koeffizient
 positiv ist, folgt mit
positiv ist, folgt mit  für die Lösung
für die Lösung  :
:
Die Ungleichung ist somit für alle
 -Werte kleiner als
-Werte kleiner als
 erfüllt.
erfüllt.
Löst man eine lineare Ungleichung mit Papier und Bleistift, so kann es einfacher
sein, alle  -Terme auf die eine Seite und alle anderen Terme auf die
andere Seite zu sortieren und anschließend die Ungleichung durch den
Koeffizienten des
-Terme auf die eine Seite und alle anderen Terme auf die
andere Seite zu sortieren und anschließend die Ungleichung durch den
Koeffizienten des  -Terms zu teilen. Dies funktioniert jedoch einerseits
nur bei linearen Ungleichungen, andererseits verlangen auch
Computer-Algebra-Systeme wie Sympy teilweise explizit
die in Gleichung (2) angegebene Darstellung.
-Terms zu teilen. Dies funktioniert jedoch einerseits
nur bei linearen Ungleichungen, andererseits verlangen auch
Computer-Algebra-Systeme wie Sympy teilweise explizit
die in Gleichung (2) angegebene Darstellung.
Quadratische Ungleichungen¶
Eine Ungleichung heißt quadratisch, wenn sie in folgender allgemeiner Form dargestellt werden kann:
(3)¶
Um eine quadratische Ungleichung zu lösen, zerlegt man den Term auf der linken
Seite, sofern möglich, in ein Produkt aus zwei Linearfaktoren. Dieses Produkt
kann nur dann negativ sein, wenn beide Faktoren unterschiedliche Vorzeichen
haben. Mittels zweier Fallunterscheidung wird also geprüft, für welche
 -Werte jeweils ein Linearfaktor positiv und der andere negativ ist; die
Lösung der quadratischen Ungleichung ist dann die Vereinigungsmenge beider
Teillösungen.
-Werte jeweils ein Linearfaktor positiv und der andere negativ ist; die
Lösung der quadratischen Ungleichung ist dann die Vereinigungsmenge beider
Teillösungen.
Lässt sich der Term auf der linken Seite nicht in Linearfaktoren zerlegen, so
ist die Ungleichung entweder für alle  -Werte wahr oder für alle
-Werte wahr oder für alle
 -Werte falsch. Welcher Fall zutrifft, lässt sich durch ein probeweises
Einsetzen eines beliebigen
-Werte falsch. Welcher Fall zutrifft, lässt sich durch ein probeweises
Einsetzen eines beliebigen  -Wertes leicht ermitteln.
-Wertes leicht ermitteln.
Betragsungleichungen¶
Ungleichungen, die einen in Betragszeichen stehenden Term  enthalten,
erfordern eine Fallunterscheidung hinsichtlich dieses Terms:
enthalten,
erfordern eine Fallunterscheidung hinsichtlich dieses Terms:
- Für alle
 -Werte, die als Bedingung
-Werte, die als Bedingung  erfüllen,
können die Betragsstriche durch runde Klammern ersetzt werden.
erfüllen,
können die Betragsstriche durch runde Klammern ersetzt werden. - Für alle
 -Werte, die
-Werte, die  zur Folge haben, werden die
Betragsstriche durch runde Klammern ersetzt und mit
zur Folge haben, werden die
Betragsstriche durch runde Klammern ersetzt und mit  multipliziert.
multipliziert.
Nach dieser Fallunterscheidung wird die verbleibende Ungleichung gelöst. In
beiden Fällen ist die Teil-Lösungsmenge gleich der Schnittmenge aus der Menge an
 -Werten, für die
-Werten, für die  beziehungsweise
beziehungsweise  ergibt,
und der jeweiligen Lösung der resultierenden Ungleichung. Die
Gesamt-Lösungsmenge ist schließlich gleich der Vereinigungsmenge beider
Teil-Lösungsmengen.
ergibt,
und der jeweiligen Lösung der resultierenden Ungleichung. Die
Gesamt-Lösungsmenge ist schließlich gleich der Vereinigungsmenge beider
Teil-Lösungsmengen.
Bruchungleichungen¶
Jede Bruchungleichung kann in eine der zwei folgenden Formen gebracht werden:
(4)¶
Im ersten Fall ist nur dann eine Lösung möglich, wenn  und
und
 beide positiv oder beide negativ sind. Im zweiten Fall muss entweder
beide positiv oder beide negativ sind. Im zweiten Fall muss entweder
 negativ und
negativ und  positiv sein, oder umgekehrt
positiv sein, oder umgekehrt  positiv
und
positiv
und  negativ. Führen die sich ergebenden Fallunterscheidungen
zu keinem Ergebnis, so ist die Ungleichung nicht lösbar.
negativ. Führen die sich ergebenden Fallunterscheidungen
zu keinem Ergebnis, so ist die Ungleichung nicht lösbar.
Beispiel:
Für welche
 -Werte gilt die folgende Ungleichung?
-Werte gilt die folgende Ungleichung?
Zunächst wird die Gleichung in die allgemeine Form (4) gebracht:
![\frac{x-2}{x+3} - 6 &< 0 {\color{white}\qquad 1}\\[3pt]
\frac{x-2}{x+3} - \frac{6 \cdot (x+3)}{x+3} &<0 \\[3pt]
\frac{x-2-6\cdot x-18}{x+3} &<0 \\[3pt]
\frac{-5 \cdot x -20}{x+3} &< 0](../_images/math/5965fabb70fb8e903fc11414da2cee839f8c9c61.png)
Die erste Möglichkeit, dass die Ungleichung erfüllt wird, besteht darin, dass der Zähler positiv und der Nenner negativ ist. Dabei muss gelten:

Die erste Teillösung lautet somit
 , da nur diese
, da nur diese
 -Werte beide Bedingungen gleichzeitig erfüllen.
-Werte beide Bedingungen gleichzeitig erfüllen.Die zweite Möglichkeit, dass die Ungleichung erfüllt wird, besteht darin, dass der Zähler negativ und der Nenner positiv ist. Dabei muss gelten:

Die zweite Teillösung lautet somit
 , da nur diese
, da nur diese
 -Werte beide Bedingungen gleichzeitig erfüllen.
-Werte beide Bedingungen gleichzeitig erfüllen.Die Gesamt-Lösung ist gleich der Vereinigungsmenge beider Teillösungen, also
![]\!-\!\infty \,;\, -4[ \;\; \cup \;\; ]\! -\!3 \,;\, +\!\infty[](../_images/math/cf4ef71ef468af9acddec5364d469e36955190e9.png) .
.
Ebenso wäre es möglich, die ursprüngliche Gleichung  mit
dem Nenner des Bruchterms zu multiplizieren; hierbei muss jedoch ebenso mittels
einer Fallunterscheidung geprüft werden, für welche
mit
dem Nenner des Bruchterms zu multiplizieren; hierbei muss jedoch ebenso mittels
einer Fallunterscheidung geprüft werden, für welche  -Werte der Nenner
positiv beziehungsweise negativ ist; anschließend muss die sich ergebende Ungleichung
mittels weiterer Fallunterscheidungen gelöst werden. Der insgesamte
Rechenaufwand wird durch dieses Verfahren also meist nicht verringert.
-Werte der Nenner
positiv beziehungsweise negativ ist; anschließend muss die sich ergebende Ungleichung
mittels weiterer Fallunterscheidungen gelöst werden. Der insgesamte
Rechenaufwand wird durch dieses Verfahren also meist nicht verringert.
Anmerkungen:
| [1] | Eine Ungleichung der Form  stellt eine Vereinigung
der Fälle stellt eine Vereinigung
der Fälle  und und  dar. Entsprechendes gilt
für Ungleichungen mit der Größer-als-Relation dar. Entsprechendes gilt
für Ungleichungen mit der Größer-als-Relation 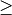 . . |
Hinweis
Zu diesem Abschnitt gibt es Übungsaufgaben.
