Aufeinander folgende Zahlen

Bei dieser Aufgabe geht es um das Lösen einer Summengleichung.

Hinweis

Das Original dieser Maxima-Beispielaufgabe kann im Original hier heruntergeladen werden. Die wxmx-Datei kann mit WxMaxima geöffnet werden.

Aufgabe:

Betrachtet wird eine Folge x _{\rm{n}} von aufeinander folgenden, ganzzahligen Werten (x,n \in \mathbb{N}).

Die Summe \sum_{i=1}^{m_1} x _{\rm{i}} der ersten m_1 Zahlen sei um einen Differenzwert d kleiner als die Summe \sum_{i=m_1+1}^{n} x _{\rm{i}} der restlichen Zahlen. Wie lässt sich diese Aufgabe mathematisch formulieren? Welche Lösung ergibt sich für n=5, m_1 = 2 und d = 42?

Lösung:

Damit die obige Bedingung erfüllt ist, muss folgende Gleichung gelten:

\sum_{i=1}^{m_1}(x_i) + d = \sum_{i=m_1+1}^{n}(x_i)

Um diese Aufgabe mit sympy zu lösen, können beide Summen in der obigen Gleichung auch in folgender Form dargestellt werden:

\sum_{i=1}^{m_1}(x + i) + d = \sum_{i=m_1+1}^{n}(x + i)

Hierbei ist der zu bestimmende Initialwert 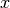x um 1 kleiner als der erste Wert der Zahlenreihe. Diese Darstellung hat den Vorteil, dass die Summen leichter formuliert werden können und die Gleichung nur noch eine Unbekannte aufweist. Der Quellcode zur Lösung der Gleichung mittels Sympy kann beispielsweise so aussehen:

import sympy as sy

# Sympy-Variablen initiieren:
n,m1,d = sy.symbols('n m1 d')
x,i = sy.symbols('x i')

# Terme festlegen
s1 = sy.summation(x + i, (i,1,m1))
s2 = sy.summation(x + i, (i,m1+1,n))

# Gleichungen formulieren:
equation = sy.Eq( s1 + d , s2)
equation_concrete = equation.subs({n:5,m1:2,d:42})

# Gleichung(en) lösen:
sy.solve(equation, x, 'dict')
sy.solve(equation_concrete, x, 'dict')

# Ergebnisse:

# Allgemein:
# [{x: (-d - m1**2 - m1 + n**2/2 + n/2)/(2*m1 - n)}]

# Konkret:
# [{x:33}]

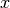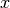Beim Lösen der Gleichung wurde hierbei explizit die Variable x als gesuchte Variable angegeben; ebenso könnte die Gleichung beispielsweise nach d für einen gegebenen Startwert x aufgelöst werden.

Das Ergebnis für die konkrete Aufgabe lautet x=33. In diesem Fall sind die n=5 Zahlen also gleich (34,35,36,37,38), die Summe der ersten m_1=2 Zahlen ist s_1=34+35=69, die Summe der weiteren Zahlen ist gleich 36+37+38 = 111.