Wurfbewegungen¶
Im folgenden Abschnitt werden zunächst eindimensionale, später auch zweidimensionale Wurfbewegungen näher beschrieben. Als Vereinfachung soll dabei der Luftwiderstand vernachlässigt werden.
Alle Wurfbewegungen haben die Gemeinsamkeit, dass die geworfenen Objekte eine
Beschleungigung von ![g=\unitfrac[9,81]{m}{s^2}](../../_images/math/4c1f726a3c213fe4ea947b680beaf5a4d2931c6d.png) („Erdbeschleunigung“) in
Richtung des Erdmittelpunkts erfahren. Die einzelnen Wurfbewegungen
unterscheiden sich also lediglich hinsichtlich ihrer Startbedingungen.
(„Erdbeschleunigung“) in
Richtung des Erdmittelpunkts erfahren. Die einzelnen Wurfbewegungen
unterscheiden sich also lediglich hinsichtlich ihrer Startbedingungen.
Freier Fall¶
Als „freien Fall“ bezeichnet man einen Bewegungsvorgang, bei dem ein Objekt mit
einer Anfangsgeschwindigkeit von 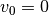 in einer Höhe
in einer Höhe 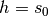 startet und konstant mit der Erdbeschleunigung
startet und konstant mit der Erdbeschleunigung ![g=
\unitfrac[9,81]{m}{s^2}](../../_images/math/be21a5926803c11de522f6b335cd37c75587f754.png) beschleunigt wird; der Luftwiderstand wird dabei
vernachlässigt.
beschleunigt wird; der Luftwiderstand wird dabei
vernachlässigt.
Durch die konstante Beschleunigung wird das fallende Objekt mit der Zeit
kontinuierlich beschleunigt. Beginnt der Vorgang zur Zeit 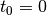 , so gilt
für die Geschwindigkeit
, so gilt
für die Geschwindigkeit  des Objekts in Abhängigkeit von der Zeit:
des Objekts in Abhängigkeit von der Zeit:
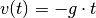
Für die zurückgelegte Wegstrecke 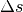 beziehungsweise den Ort
beziehungsweise den Ort
 gilt entsprechend mit
gilt entsprechend mit 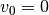 :
:
![\Delta s &= - \frac{1}{2} \cdot g \cdot t^2 \\[5pt]
s(t) &= - \frac{1}{2} \cdot g \cdot t^2 + s_0\\](../../_images/math/58d3e36a4b3d31b56cb053def03e988aaabfae8c.png)
Beim Aufprall auf dem Boden gilt 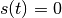 ; daraus lässt sich die Falldauer
beziehungsweise die Geschwindigkeit
; daraus lässt sich die Falldauer
beziehungsweise die Geschwindigkeit 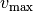 beim Aufprall
berechnen:
beim Aufprall
berechnen:
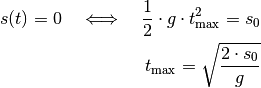
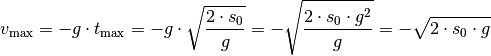
Gilt für die konstante Beschleunigung
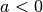 , so ist die (Halb-)Parabel
nach unten hin geöffnet.
, so ist die (Halb-)Parabel
nach unten hin geöffnet.- Ohne Anfangsgeschwindigkeit
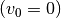 findet eine beschleunigte
Bewegung in negative
findet eine beschleunigte
Bewegung in negative  -Richtung statt.
-Richtung statt. - Mit einer Anfangsgeschwindigkeit
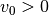 ergibt sich ein
kontinuierliches Abbremsen, wobei der Scheitel der Halbparabel den Bremsweg
angibt:
ergibt sich ein
kontinuierliches Abbremsen, wobei der Scheitel der Halbparabel den Bremsweg
angibt:
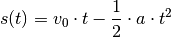
Bleibt nach einem vollständigen Abbremsen – wie bei einem senkrechten Wurf nach oben – die Beschleunigung
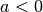 weiterhin bestehen, so findet
anschließend eine beschleunigte Bewegung in negativer
weiterhin bestehen, so findet
anschließend eine beschleunigte Bewegung in negativer  -Richtung
statt. Kann der Luftwiderstand vernachlässigt werden, so spricht man bei
diesem Vorgang von einem „freien Fall“ mit
-Richtung
statt. Kann der Luftwiderstand vernachlässigt werden, so spricht man bei
diesem Vorgang von einem „freien Fall“ mit
![|g|=\unit[9,81]{\frac{m}{s^2}}](../../_images/math/41dca893e4a3b6ed49b72ae7a1af0124829fe440.png) und
und 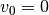 .
.- Ohne Anfangsgeschwindigkeit
Beispiel:
Der Schacht eines Brunnens hat eine Tiefe von
![h=\unit[-40]{m}](../../_images/math/5c3911c4314892c61cf5cc69a36c38463a16036d.png) . Wie
lange dauert es, bis aus der Höhe
. Wie
lange dauert es, bis aus der Höhe ![h_0 = \unit[0]{m}](../../_images/math/c0f7e39b8f67a84c059aff35c5382e381ee29d6d.png) fallender ein
Stein im freien Fall (ohne Luftwiderstand) am Grund des Schachtes ankommt? Wie
groß ist seine Geschwindigkeit
fallender ein
Stein im freien Fall (ohne Luftwiderstand) am Grund des Schachtes ankommt? Wie
groß ist seine Geschwindigkeit  beim Aufprall?
beim Aufprall?Die Bewegung des Steins entspricht einem freien Fall mit der Beschleunigung
![|g|=\unitfrac[9,81]{m}{s^2}](../../_images/math/30dc36cf46c1f422a80d99f89f5ceb991f3d8178.png) und der Anfangsgeschwindigkeit
und der Anfangsgeschwindigkeit
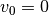 . Für die vom Stein zurückgelegte Wegstrecke
. Für die vom Stein zurückgelegte Wegstrecke 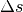 gilt
dabei:
gilt
dabei: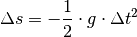
Der Vorgang endet, wenn eine Strecke von
![\Delta s=\unit[-40]{m}](../../_images/math/488fdfc5eb54d8938b2329cf462e2570e34dc8a9.png) durchlaufen wurde (das negative Vorzeichen ergibt sich, wenn eine Bewegung
nach oben als „positiv“ deklariert wird). Für die Fallzeit
durchlaufen wurde (das negative Vorzeichen ergibt sich, wenn eine Bewegung
nach oben als „positiv“ deklariert wird). Für die Fallzeit 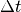 gilt also:
gilt also:![\Delta t = \sqrt{\frac{2 \cdot \Delta s}{-g}} = \sqrt{\frac{2 \cdot
(\unit[-40]{m})}{\unit[-9,81]{\frac{m}{s^2}}}} \approx \unit[2,86]{s}](../../_images/math/170b24b4e5716e918fdd059175bbfa40e9204618.png)
In dieser Zeit erreicht der Stein folgende Geschwindigkeit:
![v = -g \cdot t = -\unit[9,81]{\frac{m}{s^2}} \cdot \unit[2,86]{s} \approx
\unit[-28,0]{\frac{m}{s}}](../../_images/math/5fbc71479f584043f6ddec2fb064ee2da2b2b122.png)
Der Stein erreicht beim Aufprall unter Vernachlässigung des Luftwiderstands somit eine Geschwindigkeit von rund
![\unit[28]{\frac{m}{s}}](../../_images/math/980f0c623fb02238516dd48134c9f6971a0ead98.png) ; das
entspricht rund
; das
entspricht rund ![\unit[100]{\frac{km}{h}}](../../_images/math/99ac0bd66194f23634d5b29aec3619b2733e99fc.png) .
.
Senkrechter Wurf nach oben¶
Wird ein Objekt senkrecht nach oben geworfen, so startet es in der
 -Richtung mit einer positiven Anfangsgeschwindigkeit
-Richtung mit einer positiven Anfangsgeschwindigkeit 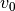 ;
gleichzeitig wird es durch die Erdbeschleunigung in die entgegengesetzte
Richtung beschleunigt. Beginnt der Vorgang wiederum zur Zeit
;
gleichzeitig wird es durch die Erdbeschleunigung in die entgegengesetzte
Richtung beschleunigt. Beginnt der Vorgang wiederum zur Zeit 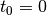 , so
gilt für die Geschwindigkeit
, so
gilt für die Geschwindigkeit  des Objekts in Abhängigkeit von der
Zeit:
des Objekts in Abhängigkeit von der
Zeit:
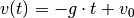
Als Annahme soll zunächst gelten, dass das Objekt in einer Höhe von 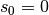 abgeworfen wird. Dann gilt für den Ort
abgeworfen wird. Dann gilt für den Ort  in Abhängigkeit von der
Zeit:
in Abhängigkeit von der
Zeit:
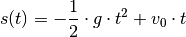
Aus den beiden obigen Gleichungen kann man die maximale Steighöhe 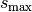 berechnen. Die zum Erreichen dieser Höhe benötigte Zeit
berechnen. Die zum Erreichen dieser Höhe benötigte Zeit
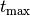 lässt sich anhand der ersten Gleichung bestimmen; an
diesem Punkt ist nämlich die Geschwindigkeit des Objekts gleich Null:
lässt sich anhand der ersten Gleichung bestimmen; an
diesem Punkt ist nämlich die Geschwindigkeit des Objekts gleich Null:
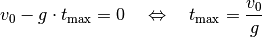
Setzt man diesen Term für 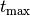 in die zweite Gleichung ein,
so kann man entsprechend die maximale Steighöhe
in die zweite Gleichung ein,
so kann man entsprechend die maximale Steighöhe 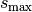 berechnen:
berechnen:
![s_{\mathrm{max}} &= v_0 \cdot t_{\mathrm{max}} - \frac{1}{2} \cdot g \cdot
t_{\mathrm{max}}^2 \\ &= v_{\mathrm{0}} \cdot \frac{v_0}{g} - \frac{1}{2}
\cdot g \cdot \left( \frac{v_0}{g}\right)^2 \\
&= \frac{\phantom{..} v_0^2 \phantom{.}}{g} - \frac{1}{2} \cdot
\frac{\phantom{..}v_0^2 \phantom{.}}{g} \\[6pt]
&= \frac{v_0^2}{2 \cdot g}](../../_images/math/903f4689fafd9745b52d3f204d6a74f6b7942e30.png)
Nach der doppelten Zeit, also 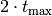 , kommt das
Objekt wieder auf dem Boden an. Dies kann man beispielsweise überprüfen,
indem man in der Weg-Zeit-Gleichung
, kommt das
Objekt wieder auf dem Boden an. Dies kann man beispielsweise überprüfen,
indem man in der Weg-Zeit-Gleichung 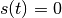 setzt und die Gleichung
nach
setzt und die Gleichung
nach  auflöst. (Der Luftwiderstand wird dabei vernachlässigt.)
auflöst. (Der Luftwiderstand wird dabei vernachlässigt.)
Die Wegstrecke wird beim Herunterfallen in der gleichen Weise durchlaufen wie
beim Hochwerfen, nur zeitlich umgekehrt. Entsprechend ist auch die
Geschwindigkeit des Objekts, sofern kein Luftwiderstand auftritt, vor
Aufprall wieder gleich der ursprünglichen Geschwindigkeit 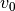 .
.
Senkrechter Wurf nach unten¶
Kann ein geworfenes Objekt – beispielsweise im Anschluss an einen
senkrechten Wurf nach oben – nach dem Erreichen seiner Ausgangslage weiter
herab fallen, so führt ab diesem diesem Zeitpunkt einen so genannten senkrechten
Wurf nach unten aus; seine Anfangsgeschwindigkeit beträgt dabei 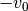 .
.
Für die Geschwindigkeit  des Objekts gilt in Abhängigkeit von
der Zeit
des Objekts gilt in Abhängigkeit von
der Zeit  :
:
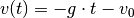
Für den Ort des Objekts gilt im zeitlichen Verlauf entsprechend:
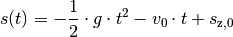
Das Koordinatensystem wurde ursprünglich so festgelegt, dass sich der Nullpunkt
der  -Achse in Höhe der Abwurfstelle, also in einer Höhe
-Achse in Höhe der Abwurfstelle, also in einer Höhe
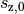 über dem Boden befindet. Das Objekt kann beim
senkrechten Wurf nach unten somit maximal die Wegstrecke
über dem Boden befindet. Das Objekt kann beim
senkrechten Wurf nach unten somit maximal die Wegstrecke 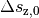 zurücklegen; erreicht es den Boden, so ist
zurücklegen; erreicht es den Boden, so ist 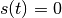 :
Damit erhält man als Gleichung:
:
Damit erhält man als Gleichung:

Diese quadratische Gleichung für 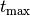 kann folgendermaßen
mit Hilfe der Lösungsformel für quadratische Gleichungen gelöst werden:
kann folgendermaßen
mit Hilfe der Lösungsformel für quadratische Gleichungen gelöst werden:
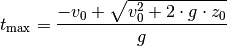
Setzt man diese Zeit  in die Geschwindigkeit-Zeit-Gleichung ein, so
folgt für die Geschwindigkeit
in die Geschwindigkeit-Zeit-Gleichung ein, so
folgt für die Geschwindigkeit  des Gegenstands unmittelbar vor dem
Aufprall auf den Boden:
des Gegenstands unmittelbar vor dem
Aufprall auf den Boden:
![v_{\mathrm{max}} &= -v_0 - g \cdot \left(\frac{-v_0 + \sqrt{v_0^2 + 2 \cdot g
\cdot z_0}}{g}\right) \\[5pt]
&= -v_0 \;\;\; - \;\; \big( -v_0 + \sqrt{v_0^2 + 2 \cdot g \cdot z_0}\big)
\\[8pt]
&= - \sqrt{v_0^2 + 2 \cdot g \cdot z_0}](../../_images/math/d2b55792ab91221f976366e390fbca68ff6bde34.png)
Gilt im Speziellen für die Anfangsgeschwindigkeit 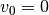 , so entspricht
das Ergebnis
, so entspricht
das Ergebnis 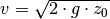 der Geschwindigkeit des
Objekts beim freien Fall.
der Geschwindigkeit des
Objekts beim freien Fall.
Waagrechter Wurf¶
Wird ein Objekt von einer erhöhten Position 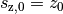 aus waagrecht geworfen, so bewegt er sich – unter Vernachlässigung des
Luftwiderstands – entlang der horizontalen
aus waagrecht geworfen, so bewegt er sich – unter Vernachlässigung des
Luftwiderstands – entlang der horizontalen 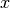 -Richtung mit seiner
ursprünglichen Geschwindigkeit
-Richtung mit seiner
ursprünglichen Geschwindigkeit 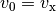 fort. In
der vertikalen Richtung findet gleichzeitig eine gleichmäßig beschleunigte
Bewegung entgegen der
fort. In
der vertikalen Richtung findet gleichzeitig eine gleichmäßig beschleunigte
Bewegung entgegen der  -Achse statt; die Anfangsgeschwindigkeit in
dieser Richtung ist
-Achse statt; die Anfangsgeschwindigkeit in
dieser Richtung ist 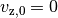 .
.
Für den Vektor 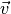 der Geschwindigkeit gilt somit in Abhängigkeit
von der Zeit
der Geschwindigkeit gilt somit in Abhängigkeit
von der Zeit  :
:
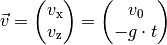
Die maximale Flugzeit 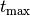 lässt sich aus der
lässt sich aus der
 -Komponente des zurückgelegten Weges bestimmen: Gilt
-Komponente des zurückgelegten Weges bestimmen: Gilt 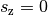 , so ist das Objekt auf dem Boden aufgekommen. Für die zugehörige Zeit
, so ist das Objekt auf dem Boden aufgekommen. Für die zugehörige Zeit
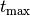 gilt somit:
gilt somit:
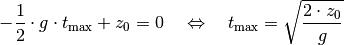
Mit diesem Ergebnis lässt sich aus der 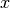 -Komponente der Bewegung die
maximale Wurfweite
-Komponente der Bewegung die
maximale Wurfweite 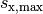 bestimmen:
bestimmen:
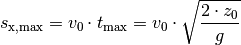
Schräger Wurf¶
Bei einem schrägen Wurf wird ein Objekt in einem Winkel  gegenüber der Horizontalen abgeworfen
gegenüber der Horizontalen abgeworfen 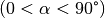 .
Für die Komponenten
.
Für die Komponenten 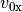 und
und 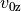 der Geschwindigkeit
der Geschwindigkeit 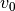 des Objekts gilt beim Abwurf:
des Objekts gilt beim Abwurf:
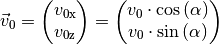
Ohne Luftwiderstand bleibt die horizontale Komponente der Geschwindigkeit
unverändert. In vertikaler Richtung wird das Objekt hingegen – wie beim
senkrechten Wurf nach oben – mit der Beschleunigung ![g=\unit[9,81]{m/s^2}](../../_images/math/b106c75dd98468445c4cf28ede45a055621785da.png) zum Erdmittelpunkt hin beschleunigt. Für die Geschwindigkeit
zum Erdmittelpunkt hin beschleunigt. Für die Geschwindigkeit 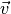 gilt somit in Abhängigkeit von der Zeit
gilt somit in Abhängigkeit von der Zeit  :
:
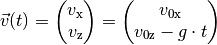
Es findet also eine Überlagerung einer Bewegung mit konstanter Geschwindigkeit
in 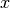 -Richtung und einer Bewegung mit konstanter Beschleunigung in
-Richtung und einer Bewegung mit konstanter Beschleunigung in
 -Richtung statt. Für die in beiden Richtungen zurückgelegten
Wegstrecken
-Richtung statt. Für die in beiden Richtungen zurückgelegten
Wegstrecken 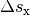 und
und 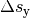 gilt:
gilt:
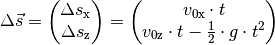
Im Folgenden wird wiederum zunächst angenommen, dass das Objekt aus einer Höhe
![s_{\mathrm{0z}} = \unit[0]{m}](../../_images/math/adf2bb50aceb4a069dbb7c280b28a8ec06261b7f.png) geworfen wird. Wie beim senkrechten Wurf
gilt dann für die Zeit
geworfen wird. Wie beim senkrechten Wurf
gilt dann für die Zeit  , in welcher der Körper die maximale Steighöhe
, in welcher der Körper die maximale Steighöhe
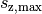 erreicht:
erreicht:
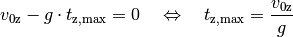
Setzt man diese Zeit in die Bewegungsgleichung für die  -Komponente
ein, so folgt für die maximale Steighöhe
-Komponente
ein, so folgt für die maximale Steighöhe 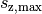 :
:
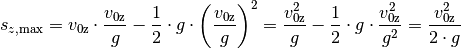
Die Wurfbahn ist (ohne Luftwiderstand) parabelförmig und damit symmetrisch; die
Zeit bis zum Aufprall auf dem Boden muss somit doppelt so lang sein wie die Zeit
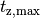 zum Erreichen der maximalen Steighöhe. In dieser Zeit
erreicht das Objekt in horizontaler Richtung folgende Entfernung:
zum Erreichen der maximalen Steighöhe. In dieser Zeit
erreicht das Objekt in horizontaler Richtung folgende Entfernung:
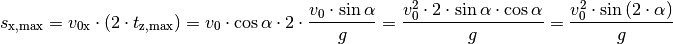
Hierbei wurde im letzten Rechenschritt das Additionstheorem für Sinus-Funktionen
genutzt. Die Wurfweite ist also – ebenfalls wie die Wurfhöhe – vom
Wurfwinkel  abhängig. Für
abhängig. Für 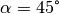 ist im
obigen Fall
ist im
obigen Fall 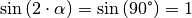 und somit die
Wurfweite maximal
und somit die
Wurfweite maximal 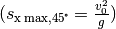 .
.
