Radioaktivität¶
Als Radioaktivität bezeichnet man die Eigenschaft von bestimmten Nukliden, sich ohne äußere Einwirkung in ein neues Nuklid (oder mehrere neue Nuklide) umzuwandeln; dabei wird Strahlung freigesetzt.
Stabilität von Atomkernen¶
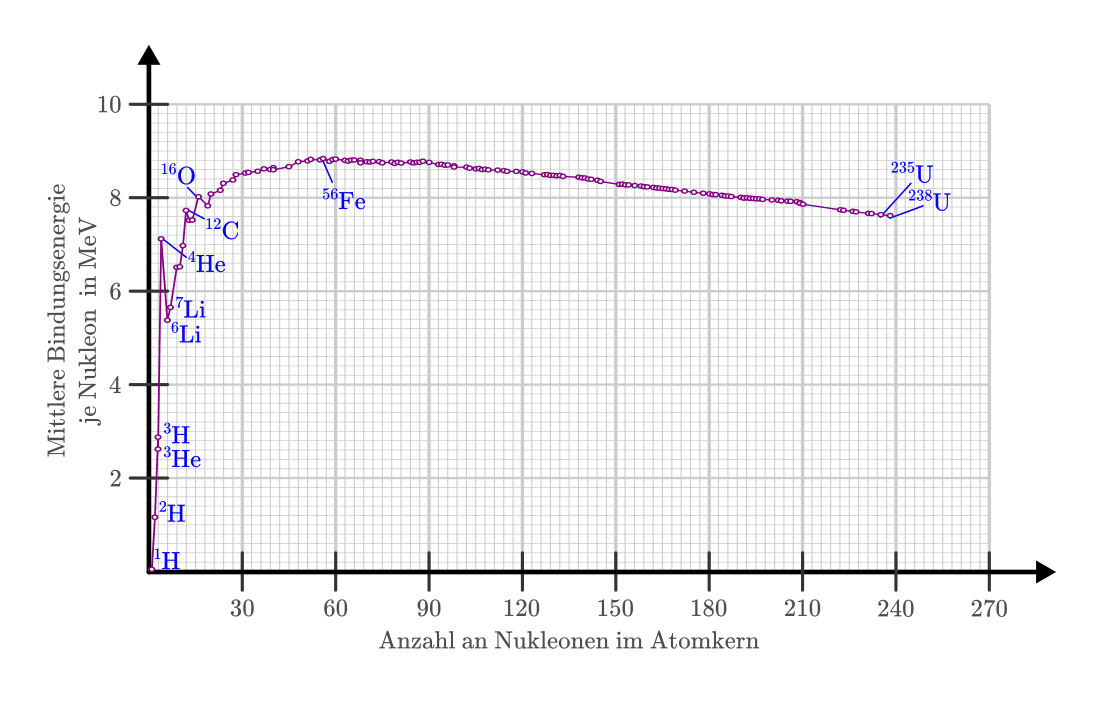
Große Atomkerne mit mehr Nukleonen haben mehr Teilchen im Kerninneren als kleine Kerne, die fast nur Außen-Nukleonen aufweisen. Damit haben die Nukleonen großer Kerne durchschnittlich auch mehr Nachbar-Nukleonen, zwischen denen anziehende Kernkräfte wirken. Dadurch nimmt zunächst mit einer steigenden Anzahl an Nukleonen auch die Bindungsenergie je Nukleon zu, wie in der folgenden Abbildung zu sehen ist:
Die am Anfang der Bindungsenergie-Kurve deutlich vorhandenen Zacken deuten darauf hin, dass auch der Atomkern eine „Schalenstruktur“ hat: Kerne mit abgeschlossenen Schalen haben besonders hohe Bindungsenergien.
Mit einer steigenden Anzahl an Protonen nehmen allerdings auch die abstoßenden
elektrostatischen Kräfte im Kern zu; diese sind nicht auf
die jeweils unmittelbaren Nachbar-Nukleonen begrenzt, sondern nehmen nur langsam
gemäß 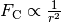 ab. Ab dem Element Eisen
(
ab. Ab dem Element Eisen
(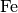 , Kernladungszahl
, Kernladungszahl 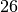 ) nimmt die Bindungsenergie je
Nukleon, und damit auch die Stabilität des Atomkerns ab. Ab dem Element Blei
(
) nimmt die Bindungsenergie je
Nukleon, und damit auch die Stabilität des Atomkerns ab. Ab dem Element Blei
(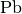 , Kernladungszahl
, Kernladungszahl 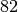 ) führt dies schließlich dazu, dass
die Kerne instabil werden.[1]
) führt dies schließlich dazu, dass
die Kerne instabil werden.[1]
Haben bei einer Kernfusion zweier leichter Atomkerne die ursprünglichen Kerne in
Summe eine höhere Bindungsenergie als der entstehende Kern, so wird bei der
Fusion – ähnlich wie bei einer chemischen Reaktion – die Differenz beider
Energiemengen frei; die Freisetzung der Energie bewirkt gemäß der Einsteinschen
Formel 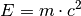 einen Massendefekt, so dass
der bei einer Fusion entstehende Kern etwas weniger Masse besitzt als die beiden
ursprünglichen Atomkerne zusammen.
einen Massendefekt, so dass
der bei einer Fusion entstehende Kern etwas weniger Masse besitzt als die beiden
ursprünglichen Atomkerne zusammen.
Arten radioaktiver Strahlung¶
Die wichtigsten Arten von radioaktiver Strahlung sowie die dafür charakteristischen Vorgänge sollen in den folgenden Abschnitten näher beschrieben werden.
Alpha-Strahlung¶
Bei einem so genannten Alpha-Zerfall emittiert der ursprüngliche Atomkern ein so
genanntes „Alpha-Teilchen“, welches dem Kern eines Helium-Atoms
(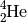 ) entspricht. Ein Alpha-Zerfall lässt sich somit allgemein
folgendermaßen beschreiben:
) entspricht. Ein Alpha-Zerfall lässt sich somit allgemein
folgendermaßen beschreiben:
(1)¶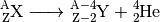
Bei einem Alpha-Zerfall sinkt also die Kernladungszahl um 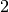 , die
Massezahl um
, die
Massezahl um 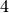 .
.
Beispiel:
Der Kern eines
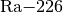 -Atoms (Radium) hat
-Atoms (Radium) hat 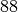 Protonen
und
Protonen
und 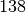 Neutronen, insgesamt also
Neutronen, insgesamt also 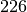 Nukleonen. Der Kern ist
instabil, er zerfällt durch einen Alpha-Zerfall. Dabei entsteht ein Radon-Kern
und ein Alpha-Teilchen:
Nukleonen. Der Kern ist
instabil, er zerfällt durch einen Alpha-Zerfall. Dabei entsteht ein Radon-Kern
und ein Alpha-Teilchen: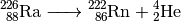
Das beim Zerfall entstehende Radon
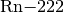 ist ebenfalls
instabil und zerfällt weiter.
ist ebenfalls
instabil und zerfällt weiter.
Die Geschwindigkeit eines emittierten Alpha-Teilchens beträgt rund
![\unit[15\,000]{\frac{km}{s}}](../_images/math/0625bd5e663d87f3ffc44cbc443e6faf643e3370.png) ; die Summe aller bei einem Zerfallsprozess
emittierten Alpha-Teilchen nennt man Alpha-Strahlen.
; die Summe aller bei einem Zerfallsprozess
emittierten Alpha-Teilchen nennt man Alpha-Strahlen.
Für die Alpha-Strahlung wird bisweilen auch  -Strahlung
geschrieben.
-Strahlung
geschrieben.
Beta-Strahlung¶
Der Begriff „Beta-Zerfall“ ist eine Sammelbezeichnung für drei mögliche radioaktive Zerfallsarten: Dem „normalen“ Beta-Minus-Zerfall, dem „Beta-Plus“-Zerfall sowie dem „Elektronen-Einfang“. Alle drei Arten werden im Folgenden kurz vorgestellt.
Beta-Minus-Strahlung
Bei einem Beta-Minus-Zerfall (oder kurz: Beta-Zerfall) wird im Kern des
ursprünglichen Atoms ein Neutron 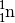 in ein Proton
in ein Proton
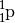 und ein Elektron
und ein Elektron 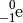 umgewandelt:
umgewandelt:
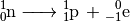
Das Proton verbleibt dabei im Kern, das Elektron wird als „Beta-Teilchen“ emittiert. Ein Beta-Minus-Zerfall lässt sich allgemein folgendermaßen beschreiben:
(2)¶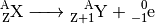
Bei einem Beta-Minus-Zerfall erhöht sich also die Kernladungszahl um 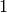 ,
die Massezahl bleibt unverändert.
,
die Massezahl bleibt unverändert.
Beispiel:
Der Kern eines
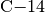 -Atoms (Kohlenstoff) hat
-Atoms (Kohlenstoff) hat 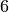 Protonen
und
Protonen
und 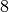 Neutronen, insgesamt also
Neutronen, insgesamt also 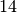 Nukleonen. Der Kern ist
instabil, er zerfällt durch einen Beta-Minus-Zerfall. Dabei entsteht ein
Stickstoff-Kern und ein Beta-Teilchen:
Nukleonen. Der Kern ist
instabil, er zerfällt durch einen Beta-Minus-Zerfall. Dabei entsteht ein
Stickstoff-Kern und ein Beta-Teilchen: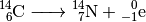
Der beim Zerfall entstehende Stickstoff
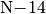 ist stabil.
ist stabil.
Die Geschwindigkeit eines emittierten Beta-Teilchens kann zwischen Null und beinahe Lichtgeschwindigkeit betragen; die Summe aller bei einem Zerfallsprozess emittierten Beta-Teilchen nennt man Beta-Minus-Strahlen.
Für die Beta-Minus-Strahlung wird bisweilen auch 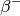 -Strahlung
geschrieben.
-Strahlung
geschrieben.
Beta-Plus-Strahlung
Bei künstlich hergestellten Radionukliden kann eine Strahlung auftreten, bei der
Teilchen emittiert werden, deren Masse mit der eines Elektrons übereinstimmt,
deren elektrische Ladung jedoch positiv ist. Derartige Teilchen werden
„Positronen“ oder 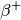 -Teilchen genannt, die entsprechende Strahlung
als „Positronstrahlung“ oder
-Teilchen genannt, die entsprechende Strahlung
als „Positronstrahlung“ oder 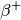 -Strahlung bezeichnet.
-Strahlung bezeichnet.
Bei einem Beta-Plus-Zerfall wird im Kern des ursprünglichen Atoms ein Proton in ein Neutron und ein Positron umgewandelt:
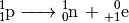
Das Neutron verbleibt dabei im Kern, das Positron wird als „Beta-Plus-Teilchen“ emittiert. Ein Beta-Plus-Zerfall lässt sich also allgemein folgendermaßen beschreiben:
(3)¶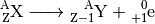
Bei einem Beta-Plus-Zerfall verringert sich also die Kernladungszahl um
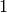 , die Massezahl bleibt unverändert.
, die Massezahl bleibt unverändert.
Beispiel:
Der Kern eines
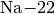 -Atoms (Natrium) hat
-Atoms (Natrium) hat 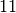 Protonen
und
Protonen
und 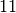 Neutronen, insgesamt also
Neutronen, insgesamt also 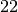 Nukleonen. Der Kern ist
instabil, er zerfällt durch einen Beta-Plus-Zerfall. Dabei entsteht ein
Neon-Kern und ein Positron:
Nukleonen. Der Kern ist
instabil, er zerfällt durch einen Beta-Plus-Zerfall. Dabei entsteht ein
Neon-Kern und ein Positron: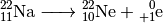
Das beim Zerfall entstehende Neon
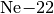 ist stabil.
ist stabil.
Für die Beta-Plus-Strahlung wird bisweilen auch 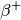 -Strahlung
geschrieben.
-Strahlung
geschrieben.
Elektronen-Einfang
Sowohl bei natürlich vorkommenden wie auch bei künstlich hergestellten Radionukliden ist eine weitere Umwandlungsart möglich: Fängt der Kern ein Elektron von der innersten Schale der Elektronenhülle ein, so kann sich im Kern ein Proton gemeinsam mit diesem Elektron in ein Neutron umwandeln:
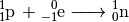
Ein Elektronen-Einfang lässt sich also allgemein folgendermaßen beschreiben:
(4)¶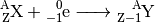
Bei einem Elektronen-Einfang verringert sich also die Kernladungszahl um
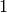 , die Massezahl bleibt unverändert. Ein Elektronen-Einfang führt also
zum gleichen Ergebnis wie die Emission eines Positrons.
, die Massezahl bleibt unverändert. Ein Elektronen-Einfang führt also
zum gleichen Ergebnis wie die Emission eines Positrons.
Beispiel:
Der Kern eines
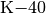 -Atoms (Kalium) hat
-Atoms (Kalium) hat 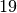 Protonen und
Protonen und
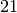 Neutronen, insgesamt also
Neutronen, insgesamt also 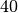 Nukleonen. Der Kern ist
instabil, er kann durch einen Elektronen-Einfang zerfallen (aber auch durch
einen
Nukleonen. Der Kern ist
instabil, er kann durch einen Elektronen-Einfang zerfallen (aber auch durch
einen 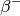 - oder
- oder 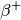 -Zerfall). Beim
Elektronen-Einfang entsteht ein Argon-Kern:
-Zerfall). Beim
Elektronen-Einfang entsteht ein Argon-Kern: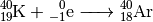
Das beim Zerfall entstehende Argon
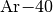 ist stabil.
ist stabil.
Der Platz in der innersten Elektronenschale, der beim Elektronen-Einfang frei wird, wird durch ein Elektron aus dem äußeren Teil der Elektronenhülle des jeweiligen Atoms wieder aufgefüllt. Dabei entsteht eine für den jeweiligen Zerfall charakteristische Gamma-Strahlung.
Gamma-Strahlung¶
Gammastrahlung entsteht, wenn Atomkerne energiereiche Lichtquanten (so genannte
„Gamma-Quanten“) aussenden; dabei ändert sich weder die Massenzahl  noch die Kernladungszahl
noch die Kernladungszahl 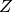 des Atomkerns. Gammastrahlen entstehen
vielmehr durch einen Übergang eines Atomkerns von einem energetisch angeregten
Zustand in einen energetisch niedrigeren Zustand. So entsteht bei Alpha- und
Beta-Zerfällen häufig zusätzlich Gamma-Strahlung.
des Atomkerns. Gammastrahlen entstehen
vielmehr durch einen Übergang eines Atomkerns von einem energetisch angeregten
Zustand in einen energetisch niedrigeren Zustand. So entsteht bei Alpha- und
Beta-Zerfällen häufig zusätzlich Gamma-Strahlung.
Nachweis radioaktiver Strahlung¶
Radioaktive Strahlen können auf mehrere Arten nachgewiesen werden:
Entladungsdosimeter
Radioaktive Strahlen können Luft ionisieren, indem sie Elektronen aus den Luftmolekülen herausschlagen. Wird die Luft zwischen zwei geladenen Kondensator-Platten ionisiert, so kann sich der Kondensator langsam entladen. Je stärker die Strahlung ist, desto stärker ist auch die Ionisation und somit die Entladung des Kondensators. Entladungsdosimeter reagieren alle oben genannten Strahlungsarten.
Filmdosimeter
Bei einem Filmdosimeter wird als Nachweisprinzip genutzt, dass radioaktive Strahlung spezielle Filme belichten („schwärzen“) kann. Solche Filmdosimeter können beispielsweise als Plaketten an Laborkitteln angebracht werden; sie können bei der Auswertung zwar die Menge der insgesamt aufgetroffenen Strahlung aufzeigen, geben jedoch keine genaue Auskunft über die Art der auftreffenden Strahlung oder über den zeitlichen Verlauf der Einwirkung.
Nebelkammer
Im Jahr 1911 bestrahlte Charles Wilson im Rahmen von metereologischen Untersuchungen einen mit unsichtbarem Wasserdampf übersättigten Raum mit Alpha- und Betastrahlen. Er stellte fest, dass diese die auf ihrem Weg liegenden Luftmoleküle ionisieren, und dabei als Kondensationskerne wirken: An den elektrisch geladenen Luftteilchen lagern sich sichtbare Wasser-Tröpfchen an, so dass die Bahn der Alpha- und Beta-Teilchen in Form von „Kondensstreifen“ erkennbar wird.
Geigerzähler
Im Jahr 1928 entwickelten Hans Geiger und Walther Müller eine Apparatur, welche die
ionisierende Wirkung von Gammastrahlen als akustische Geräusche hörbar machte.
Ein solches Geiger-Müller-Zählrohr („Geigerzähler“) besteht aus einem
Metallrohr, in dem ein dünner Metallfaden gespannt ist. Der Metallfaden ist
elektrisch vom Metallrohr isoliert; zwischen dem Draht und der Rohrwand liegt
eine Spannung von rund ![\unit[500]{V}](../_images/math/ac4868569a54d9ff7aaa367f6eb57fb8914d8fb9.png) an. Das Rohr ist mit einem sehr
dünnen Fenster aus Glimmer verschlossen, durch das Strahlung ins Innere des
Rohres gelangen kann.
an. Das Rohr ist mit einem sehr
dünnen Fenster aus Glimmer verschlossen, durch das Strahlung ins Innere des
Rohres gelangen kann.
Trifft ein Gamma-Quant im Inneren des Rohres auf ein Luftteilchen, so wird
dieses durch das Herausschlagen eines Elektrons zu einem positiven Ion. Durch
das elektrische Feld wird das entstehende positive Ion derart stark beschleunigt,
dass es durch Stöße mit anderen Luftteilchen weitere freie Ladungsträger erzeugt
(„Stoßionisation“). Die Luft wird also dadurch leitend, und es fließt kurzzeitig
ein Strom über den Widerstand 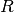 . Der kurzzeitige Stromfluss kann bei
Verwendung eines geeigneten Verstärkers mittels eines Lautsprechers als
„Knacken“ hörbar gemacht werden.
. Der kurzzeitige Stromfluss kann bei
Verwendung eines geeigneten Verstärkers mittels eines Lautsprechers als
„Knacken“ hörbar gemacht werden.
Durch den Stromfluss nimmt jedoch die Spannung am Zählrohr um den Betrag
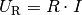 ab. Das Gas im Zählrohr wird in Folge dessen
wieder zu einem Isolator; der Prozess kann erneut beginnen.
ab. Das Gas im Zählrohr wird in Folge dessen
wieder zu einem Isolator; der Prozess kann erneut beginnen.
Szintillationszähler
Bei einem Szintillationszähler trifft die Strahlung auf eine Leuchtstoff-Scheibe. Jedes Strahlungsquant erzeugt dort einen Lichtblitz. Jeder Lichtblitz wird genutzt, um mittels einer Foto-Diode einen kurzzeitigen Stromfluss zu erzeugen, der wiederum über eine entsprechende Verstärker-Schaltung von einer Zählautomatik ausgewertet wird.
Halbwertszeit und Aktivität¶
Für einen einzelnen Atomkern lässt sich keine Aussage darüber treffen, zu welchem Zeitpunkt er zerfallen wird: Er kann in der nächsten Sekunde oder erst in Tausenden von Jahren zerfallen.
Für eine große Anzahl an Atomkernen hingegen kann man eine Wahrscheinlichkeits-Aussage über den Ablauf des Zerfalls treffen. Die Zeit, nach der die Hälfte einer bestimmten Anzahl an Atomkernen zerfallen ist, wird Halbwertszeit genannt. Für jedes Radionuklid ist diese Zeit eine charakteristische Größe; je nach Element reichen die Halbwertszeiten von nur wenigen Sekunden bishin zu Millionen von Jahren.
| Element | Symbol | Zerfallsart | Halbwertszeit |
| Polonium-214 | 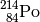 |
 |
![\unit[1,64 \cdot 10^{-4}]{s}](../_images/math/bb7383d4ac78a04d67fd771915f7a3d2ee34cbb8.png) |
| Radon-220 | 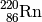 |
 |
![\unit[55,6]{s}](../_images/math/33390c17d4a644d7cfc5d48f04140c242f750406.png) |
| Polonium-218 | 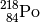 |
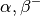 |
![\unit[3,05]{min}](../_images/math/d2146db62ee6a8a7cfde4bad1a391d496e4a25d1.png) |
| Wismut-214 | 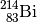 |
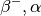 |
![\unit[19,9]{min}](../_images/math/63d4c343bc969421b4cdbaf83840bc2f47309cc6.png) |
| Blei-214 | 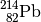 |
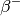 |
![\unit[26,8]{min}](../_images/math/2de14563dda9a26ba0ef1b3a6b88e195d994358b.png) |
| Blei-209 | 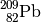 |
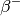 |
![\unit[3,25]{h}](../_images/math/bcf37494fc1a0cac3cd87b3b74868460e66cf2f5.png) |
| Radon-222 | 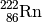 |
 |
![\unit[3,83]{d}](../_images/math/b1e35e8517c7625c90c200a8cb334105e2f01a48.png) |
| Radium-223 | 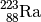 |
 |
![\unit[11,43]{d}](../_images/math/9501b730e0b33dbc9a8eb3310f8d335e13ca2019.png) |
| Radium-225 | 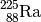 |
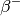 |
![\unit[14,8]{d}](../_images/math/f586e0068e877a753ac1ef03a5f848469332a58c.png) |
| Thorium-234 | 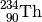 |
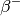 |
![\unit[24,1]{d}](../_images/math/f74c87f8f59796f2ed1658751185e9890d28b982.png) |
| Polonium-210 | 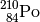 |
 |
![\unit[138,4]{d}](../_images/math/1a00fb14437a3693232a27ee89be61ca76daf60f.png) |
| Wasserstoff-3 | 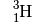 |
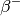 |
![\unit[12,32]{a}](../_images/math/338409999ca23395fba829f1ff50ec3f406312fe.png) |
| Blei-210 | 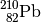 |
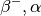 |
![\unit[22,3]{a}](../_images/math/09797baa359b15538aef69a7f8f4499d1901f1cc.png) |
| Strontium-90 | 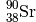 |
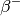 |
![\unit[28,5]{a}](../_images/math/c70599cf009183e522175bb0d8942a8105d9bcad.png) |
| Radium-226 | 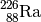 |
 |
![\unit[1,6 \cdot 10^{3}]{a}](../_images/math/e4beffdcdfff9e302104bf9b34180740ce98b43f.png) |
| Kohlenstoff-14 |  |
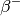 |
![\unit[5,73 \cdot 10^{3}]{a}](../_images/math/c6afd6d95d22f1d39e918077364c4a7cdfb5a091.png) |
| Uran-235 | 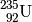 |
 |
![\unit[7,04 \cdot 10^{8}]{a}](../_images/math/c34c2ed6ce0621479b6d4f00be7be3231f87d5a9.png) |
| Kalium-40 |  |
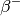 |
![\unit[1,28 \cdot 10^{9}]{a}](../_images/math/404b9a771b25c244eb7c07639e9bdfd376bcb593.png) |
| Uran-280 | 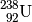 |
 |
![\unit[4,47 \cdot 10^{9}]{a}](../_images/math/482892f70c472f91dbc458cefa4830493d0234c3.png) |
| Thorium-232 | 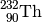 |
 |
![\unit[1,41 \cdot 10^{10}]{a}](../_images/math/08703fa73e8723d923465a5d7bcf859e64ed6550.png) |
Je Halbwertszeit zerfällt die Hälfte der jeweils zu Beginn noch vorhandenen
Atomkerne. Die Anzahl der radioaktiven Kerne nimmt also exponentiell (zunächst
schnell, dann immer langsamer) ab. Wird die Anzahl der zu Beginn eines Zerfalls
vorhandenen Radionuklide mit 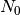 und die Halbwertszeit mit
und die Halbwertszeit mit 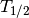 bezeichnet, so kann die Anzahl
bezeichnet, so kann die Anzahl 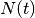 an zur Zeit
an zur Zeit
 noch vorhandenen Atomkernen nach folgendem „Zerfallsgesetz“ berechnet
werden:
noch vorhandenen Atomkernen nach folgendem „Zerfallsgesetz“ berechnet
werden:
(5)¶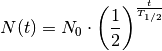
Nach vier Halbwertszeiten sind die Atome eines Radionuklid zu mehr als
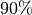 , nach zehn Halbwertszeiten zu mehr als
, nach zehn Halbwertszeiten zu mehr als 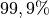 zerfallen.
zerfallen.
Definition:
Als Aktivität
bezeichnet man die Anzahl
an Kernumwandlungen, die innerhalb einer bestimmten Zeitspanne
stattfinden:
(6)¶
Einheit:
Die Einheit der Aktivität ist nach Henry Becquerel benannt. Nach der obigen Gleichung ergibt sich für
![\unit[1]{Becquerel}](../_images/math/9c1e53f4584f2005012eea7d67e43e2ac7c1bf61.png)
folgender Zusammenhang:[2]
Auf natürliche Weise treten in geschlossenen Räumen je Kubikmeter Luft rund
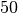 Zerfälle je Sekunde auf, die Aktivität beträgt somit je Kubikmeter
rund
Zerfälle je Sekunde auf, die Aktivität beträgt somit je Kubikmeter
rund ![\unit[50]{Bq}](../_images/math/076f89cac3aac7b4994a24d45285db2c1d814c68.png) . In einem Gramm „natürlichem“ Uran hingegen, wie es
im Bergbau abgebaut werden kann, treten rund
. In einem Gramm „natürlichem“ Uran hingegen, wie es
im Bergbau abgebaut werden kann, treten rund 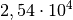 Zerfälle
je Sekunde auf.
Zerfälle
je Sekunde auf.
Ionendosis, Energiedosis und Äquivalentdosis¶
Die durch Strahlung transportierte Energie ist sehr viel kleiner als
![\unit[1]{Joule}](../_images/math/187b67562a193664c8fc2f124b6582c5798d01ff.png) ; man verwendet daher als Energie-Einheit das so genannte
Elektronenvolt
; man verwendet daher als Energie-Einheit das so genannte
Elektronenvolt 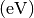 . Damit bezeichnet man diejenige Energiemenge,
die ein Elektron beim Durchlaufen einer Spannung von
. Damit bezeichnet man diejenige Energiemenge,
die ein Elektron beim Durchlaufen einer Spannung von ![\unit[1]{V}](../_images/math/e574e4eb55da20a40731e2ac32107d6beb267541.png) aufnimmt. Für die Umrechnung gilt:
aufnimmt. Für die Umrechnung gilt:
![\unit[1]{eV} = \unit[1,602 \cdot 10^{-19}]{J}](../_images/math/7df0e7912fb711d5610a1bc1e81bac5b34ba6d13.png)
Gasatome beziehungsweise Gasmoleküle haben beispielsweise bei Zimmertemperatur
eine Bewegungsenergie von etwa ![\unit[0,04]{eV}](../_images/math/aa6ec3f49a6c13e77315706c399b41829aabcc78.png) .
.
Um bei der Ionisierung eines Wasserstoff-Atoms 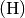 das Elektron aus
der Atomhülle abzutrennen, ist eine Energiemenge von
das Elektron aus
der Atomhülle abzutrennen, ist eine Energiemenge von ![\unit[13,60]{eV}](../_images/math/9b5775758ba04eed2f12e55c1438ead482ea7432.png) erforderlich; um ein Elektron bei einem Wasserstoff-Molekül
erforderlich; um ein Elektron bei einem Wasserstoff-Molekül 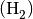 abzutrennen, ist eine Energiemenge von
abzutrennen, ist eine Energiemenge von ![\unit[15,40]{eV}](../_images/math/2d802947fb2f616d49d3bffbdfa0acf454893567.png) nötig. Diese so
genannte „Ionisierungsenergie“ ist bei verschiedenen Elementen für die einzelnen
Elektronen der Atomhülle unterschiedlich.
nötig. Diese so
genannte „Ionisierungsenergie“ ist bei verschiedenen Elementen für die einzelnen
Elektronen der Atomhülle unterschiedlich.
Die Ionisation von Atomen ist das wichtigste Maß für die Intensität von radioaktiver Strahlung, denn diese kann nur gemessen werden, wenn Wechselwirkungen der Strahlung mit Materie stattfinden.
Definition:
Die sogenannte Ionendosis
gibt an, wie groß die durch Ionisierung erzeugte Ladungsmenge
im Verhältnis zur Masse
des durchstrahlten Materials ist:
Einheit:
Die Basis-Einheit der elektrischen Ladung ist das Coulomb; damit ergibt sich nach der obigen Gleichung für die Einheit der Ionendosis:
… to be continued …
Anmerkungen:
| [1] | Die elektrostatische Abstoßung der Protonen ist ebenfalls der Grund dafür, dass schwere Atomkerne mehr Neutronen als Protonen besitzen; diese schirmen die abstoßenden Kräfte zum Teil ab. |
| [2] | In alten Büchern wurde zudem häufig die nach Piere und Marie Curie benannte Einheit Curie
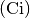 verwendet. Als Umrechnung gilt verwendet. Als Umrechnung gilt ![\unit[1]{Ci} =
\unit[3,7 \cdot 10^{10}]{Bq}](../_images/math/d27ff34ba2b7ed4d5836f6ced2b165e7d8bae824.png) ; diese Einheit sollte jedoch nicht weiter
verwendet werden, um die Menge an üblichen Einheiten möglichst gering zu
halten. ; diese Einheit sollte jedoch nicht weiter
verwendet werden, um die Menge an üblichen Einheiten möglichst gering zu
halten. |

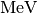 .
.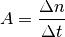
![\unit[1]{Bq} = \unit[1]{\frac{1}{s}}](../_images/math/2fb2190f030f0e8c98f302c7432bce2a81c7118e.png)
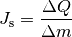
![[ J_{\mathrm{s}}] = \unit{\frac{C}{kg}}](../_images/math/cc79d9f15699a1887cf8f009c1a4922ab72042b2.png)