Algebraische Strukturen

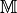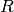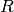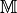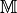Fasst man eine Menge \mathbb{M} und eine Relation R zu einem geordneten Paar [\mathbb{M} ;\; R] zusammen, so wird dadurch dargestellt, dass die Relation R in der Menge \mathbb{M} erklärt ist. Entsprechend bedeutet [ \mathbb{M} ;\; \mathrm{Op}], dass in der Menge \mathbb{M} die Operation 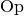\mathrm{Op} erklärt ist. In beiden Fällen spricht man von einer (algebraischen) Struktur.

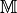Bildet man nach dem gleichen Prinzip ein geordnetes Paar [\mathbb{M} ;\; R_1 ,\, \ldots ,\, R _{\mathrm{n}} ;\; \mathrm{Op}_1 ,\, \ldots ,\, \mathrm{Op}_{\mathrm{n}}], das aus einer nichtleeren „Trägermenge“ \mathbb{M} sowie den Relationen R_1 ,\, \ldots ,\, R_{\mathrm{n}} und den Operationen \mathrm{Op}_1 ,\, \ldots ,\, \mathrm{Op} _{\mathrm{n}} besteht, so spricht man von einem (algebraischen) Bereich.

Trotz des begrifflichen Unterschieds ist es üblich, einen Bereich und seine Trägermenge mit dem selben Symbol darzustellen. Die wichtigsten Bereiche beziehungsweise Mengen der allgemeinen Mathematik sind:

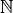  • \mathbb{N}: Die Menge (beziehungsweise der Bereich) der natürlichen Zahlen
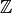  • \mathbb{Z}: Die Menge (beziehungsweise der Bereich) der ganzen Zahlen
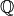  • \mathbb{Q}: Die Menge (beziehungsweise der Bereich) der rationalen Zahlen
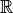  • \mathbb{R}: Die Menge (beziehungsweise der Bereich) der reellen Zahlen
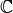  • \mathbb{C}: Die Menge (beziehungsweise der Bereich) der komplexen Zahlen