Mathematik mit Standard-Modulen¶
In jeder Python-Installation ist das Standard-Modul math enthalten. Es enthält zahlreiche Funktionen, die aus dem Python-Interpreter einen umfangreichen und programmierbaren Taschenrechner machen.
Das math-Modul wird meistens in folgender Form eingebunden:
import math as m
Anschließend kann so das math-Modul unter der Bezeichnung m angesprochen
werden; dies spart Tipp-Arbeit. Als einzige (verkraftbare) Einschränkung hat
dies zur Folge, dass keine andere Variable mit m benannt werden darf.
Das math-Modul enthält unter anderem folgende Funktionen, die jeweils auf
einzelne Zahlenwerte angewendet werden können:
m.pow(zahl,n) |
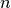 -te Potenz einer Zahl (oder -te Potenz einer Zahl (oder 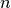 -te Wurzel wenn -te Wurzel wenn 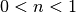 ) ) |
m.sqrt(zahl) |
Quadrat-Wurzel einer positiven Zahl |
m.exp(x) |
Exponentialfunktion 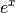 mit
Exponent mit
Exponent 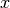 |
m.log(x, a) |
Logarithmusfunktion
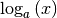 von von 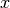 zur Basis zur Basis  |
m.radians(winkelwert) |
Winkelumrechnung von Grad auf Radians |
m.degrees(winkelwert) |
Winkelumrechnung von Radians auf Grad |
m.sin(x), m.cos(x) und m.tan(x) |
Trigonometrische Funktionen für 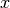 -Werte in Radians -Werte in Radians |
m.asin(x), m.acos(x) und m.atan(x) |
Umkehrfunktionen der trigonometrischen Funktionen (Ergebnisse in Radians) |
math.floor(zahl) |
Nächst kleinerer int-Wert 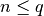 einer Zahl einer Zahl 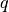 |
math.ceil(zahl) |
Nächst größerer int-Wert 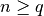 einer Zahl einer Zahl 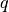 |
Zudem sind im math-Modul die Konstanten m.pi und m.e für die
Kreiszahl 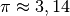 beziehungsweise die Eulersche Zahl
beziehungsweise die Eulersche Zahl 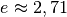 vordefiniert.
vordefiniert.
Neben dem math-Modul existieren weiter für mathematische Zwecke nützliche
Module, beispielsweise cmath für das Rechnen mit komplexen
Zahlen oder functools für das Anwenden von Operatoren
und/oder Funktionen auf eine ganze Liste von Zahlen. Im folgenden werden einige
Anwendungsbeispiele vorgestellt, die sich an den Aufgaben zur Arithmetik orientieren.
Primfaktor-Zerlegung
Um die Primfaktoren einer ganzen Zahl 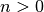 zu bestimmen, kann man
folgende Funktion nutzen (Quelle: StackOverflow):
zu bestimmen, kann man
folgende Funktion nutzen (Quelle: StackOverflow):
def prim(n):
'''Calculates all prime factors of the given integer.'''
from math import sqrt
pfactors = []
limit = int(sqrt(n)) + 1
check = 2
num = n
if n == 1:
return [1]
for check in range(2, limit):
while num % check == 0:
pfactors.append(check)
num /= check
if num > 1:
pfactors.append(num)
return pfactors
Die Grund-Idee von diesem Algorithmus liegt darin, dass eine Zahl keinen
Primzahl-Faktor haben kann, der größer ist als die Quadratwurzel dieser Zahl.
Für 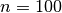 ist beispielsweise
ist beispielsweise 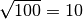 der größtmögliche
Faktor, der eine Primzahl sein könnte.
der größtmögliche
Faktor, der eine Primzahl sein könnte.
- Andere Produkte mit größeren Faktoren
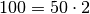 lassen sich
zwar ebenfalls bilden, enthalten dann allerdings stets einen Faktor, der
kleiner als die Quadrat-Wurzel der Original-Zahl ist.
lassen sich
zwar ebenfalls bilden, enthalten dann allerdings stets einen Faktor, der
kleiner als die Quadrat-Wurzel der Original-Zahl ist. - Die einzelnen möglichen Primfaktoren lassen sich finden, indem man
nacheinander die Faktoren
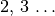 in aufsteigender Reihenfolge
durchprobiert. Um eine mögliche Mehrfachheit einzelner Faktoren nicht außer
Acht zu lassen, muss bei jedem gefundenen Faktor geprüft werden, ob sich die
Original-Zahl gegebenenfalls auch mehrfach durch diesen dividieren lässt.
in aufsteigender Reihenfolge
durchprobiert. Um eine mögliche Mehrfachheit einzelner Faktoren nicht außer
Acht zu lassen, muss bei jedem gefundenen Faktor geprüft werden, ob sich die
Original-Zahl gegebenenfalls auch mehrfach durch diesen dividieren lässt. - Ist ein Faktor gefunden, so kann man die Original-Zahl durch diesen dividieren und den Algorithmus erneut mit dem resultierenden Divisions-Rest fortsetzen.
Die gefundenen Faktoren sind tatsächlich allesamt Primzahlen: Jeder andere Faktor ließe sich selbst als Produkt jeweils kleinerer Primzahlen darstellen. Die Teilbarkeit durch diese Zahlen wurde im Lauf des Algorithmus allerdings bereits geprüft; der jeweilige Divisionsrest, mit dem der Algorithmus fortfährt, enthält diese Faktoren nicht mehr.
Mittels der obigen Funktion kann nun die Primzahl einer Zahl oder eines Zahlenbereichs folgendermaßen berechnet werden:
# Einzelne Zahl in Primfaktoren zerlegen:
prim(2017)
# Zahlenbereich in Primfaktoren zerlegen:
for n in range(1,1000):
print(prim(n))
Größter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches
Beim Rechnen mit rationalen Zahlen, insbesondere beim Kürzen eines Bruchterms oder beim Multiplizieren zweier Brüche, ist es nützlich, den größten gemeinsamen Teiler zweier Zahlen zu finden. Hierzu wird bis heute ein Algorithmus verwendet, den bereits Euklid in der Antike entdeckt hat:
Hat man zwei Zahlen
 und
und 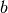 mit
mit 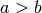 , so ist der größte
gemeinsame Teiler von
, so ist der größte
gemeinsame Teiler von  und
und 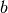 identisch mit dem größten
gemeinsamen Teiler von
identisch mit dem größten
gemeinsamen Teiler von  und
und 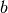 . Man kann also wiederholt
immer wieder die kleinere Zahl von der größeren abziehen und das Prinzip
erneut anwenden, solange bis man beim größten gemeinsamen Teiler
angekommen ist.
. Man kann also wiederholt
immer wieder die kleinere Zahl von der größeren abziehen und das Prinzip
erneut anwenden, solange bis man beim größten gemeinsamen Teiler
angekommen ist.Ist beispielsweise
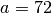 und
und 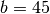 , so ist der größte gemeinsame
Teiler dieser beider Zahlen identisch mit dem der Zahlen
, so ist der größte gemeinsame
Teiler dieser beider Zahlen identisch mit dem der Zahlen 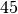 und
und
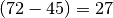 . erneut kann man die Differenz beider Zahlen bilden und
erhält damit das Zahlenpaar
. erneut kann man die Differenz beider Zahlen bilden und
erhält damit das Zahlenpaar 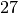 und
und 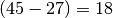 ; ein
wiederholtes Anwenden des gleichen Prinzips liefert das zunächst das
Zahlenpaar
; ein
wiederholtes Anwenden des gleichen Prinzips liefert das zunächst das
Zahlenpaar 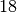 und
und 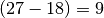 und schließlich
und schließlich 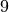 und
und
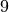 ; der größte gemeinsame Teiler beider Zahlen ist somit
; der größte gemeinsame Teiler beider Zahlen ist somit 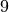 .
.Ist die eine Zahl
 wesentlich größer als die andere Zahl
wesentlich größer als die andere Zahl 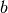 ,
so müsste bei Anwendung des vorherigen Algorithmus sehr oft
,
so müsste bei Anwendung des vorherigen Algorithmus sehr oft 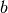 von
von
 subtrahiert werden. Ist beispielsweise
subtrahiert werden. Ist beispielsweise 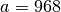 und
und
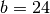 , so ergäbe die erste Differenz
, so ergäbe die erste Differenz 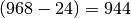 , die zweite
Differenz
, die zweite
Differenz 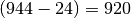 , usw. Bei Verwendung eines Computers ist es
effektiver, anstelle der wiederholten Subtraktion eine Modulo-Rechnung
vorzunehmen, also bei einer Division mit Rest nur auf den Divisionsrest zu
achten. Hier ergibt
, usw. Bei Verwendung eines Computers ist es
effektiver, anstelle der wiederholten Subtraktion eine Modulo-Rechnung
vorzunehmen, also bei einer Division mit Rest nur auf den Divisionsrest zu
achten. Hier ergibt 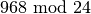 den Wert
den Wert 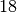 ; der
Algorithmus kann somit unmittelbar mit
; der
Algorithmus kann somit unmittelbar mit 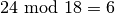 fortgeführt werden und liefert schon im dritten Schritt als Ergebnis
fortgeführt werden und liefert schon im dritten Schritt als Ergebnis 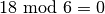 . Der größte gemeinsame Teiler
. Der größte gemeinsame Teiler 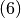 wurde so in nur
drei Rechenschritten bestimmt.
wurde so in nur
drei Rechenschritten bestimmt.
In Python lässt sich diese zweite, schnellere Variante des Euklidschen
Algorithmus dank des Modulo-Operators % mit nur sehr wenig Code
implementieren.
def gcd_simple(a, b):
'''Quite simple implementation of Euclid's Algorithm.'''
while b != 0:
tmp = a % b
a = b
b = tmp
return a
Dieser Code lässt sich noch weiter optimieren. Der Trick der folgenden
Implementierung besteht darin, dass der Zuweisungsoperator = eine geringere
Priorität besitzt als der Modulo-Operator, und somit erst die rechte Seite
ausgewertet wird, bevor die Ergebnisse in die links angegebenen Variablen
gespeichert werden; dies erspart das Speichern der Zwischenergebnisse in
temporären Variablen:
def gcd(a, b):
'''Return the greatest common divisor using Euclid's Algorithm.'''
while b:
a, b = b, a % b
return a
Hat man den größten gemeinsamen Teiler gefunden, so kann auch das kleinste gemeinsame Vielfache zweier Zahlen einfach berechnet werden: Man multipliziert beide Zahlen miteinander und dividiert das Ergebnis anschließend durch den größten gemeinsamen Teiler. In Python könnte die entsprechende Funktion also folgendermaßen aussehen:
def lcm(a, b):
'''Return lowest common multiple.'''
return a * b / gcd(a, b)
Möchte man das kleinste gemeinsame Vielfache nicht nur zweier, sondern einer
Liste mit beliebig vielen ganzen Zahlen ermitteln, so müsste man die obige
lcm()-Funktion iterativ auf die einzelnen Elemente der Liste anwenden. Nutzt
man hierfür die Funktion reduce() aus dem Standard-Modul functools, so lässt sich der Algorithmus folgendermaßen implementieren
(Quelle: Stackoverflow):
import functools as ft
def lcmm(*args):
'''turn lcm of args.'''
return ft.reduce(lcm, args)
# Beispiel:
lcmm(6, 13, 27, 84)
# Ergebnis: 9828
… to be continued …
