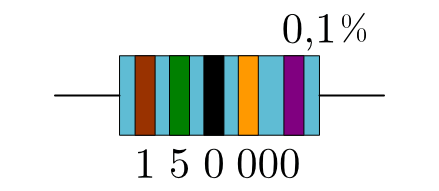Lösungen zu elektronischen Bauteilen¶
Widerstände¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Widerstände.
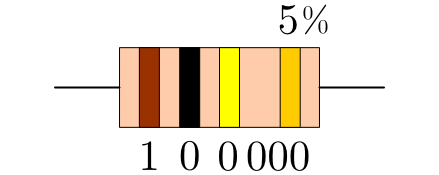
Der erste Ring ist braun, somit ist die erste Ziffer des Widerstandswertes gleich
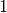 . Der zweite Ring ist schwarz, somit ist die zweite Ziffer
des Widerstandswertes gleich
. Der zweite Ring ist schwarz, somit ist die zweite Ziffer
des Widerstandswertes gleich 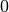 . Der dritte Ring ist gelb, somit sind
vier Nullen an den Zahlenwert anzuhängen. Insgesamt ergibt sich somit ein
Widerstandswert von
. Der dritte Ring ist gelb, somit sind
vier Nullen an den Zahlenwert anzuhängen. Insgesamt ergibt sich somit ein
Widerstandswert von ![\unit[100\,000]{\Omega } = \unit[100]{k \Omega }](../_images/math/497d3511c02cf0ae94c6962aea2b2ca1526c90ac.png) .
.Der goldfarbene Ring am rechten Rand zeigt an, dass der Toleranzbereich bei
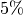 liegt. Der tatsächliche Wert des Widerstands liegt somit
zwischen
liegt. Der tatsächliche Wert des Widerstands liegt somit
zwischen ![\unit[95]{k \Omega }](../_images/math/85dbcc060877901c0454b5513e31292f6c2d320e.png) und
und ![\unit[105]{k \Omega }](../_images/math/ba41ba76e7c9e3d92dd9c8174ff3520fc8085504.png) .
.
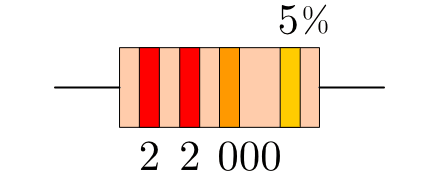
Die ersten beiden Ringe des Widerstands sind rot, somit haben die ersten beiden Ziffern des Widerstandswertes jeweils den Wert
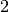 . Der dritte
Ring ist orange, so dass an den Zahlenwert drei Nullen anzuhängen sind. Der
Widerstand hat somit einen Wert von
. Der dritte
Ring ist orange, so dass an den Zahlenwert drei Nullen anzuhängen sind. Der
Widerstand hat somit einen Wert von ![\unit[22\,000]{\Omega } =
\unit[22]{k \Omega }](../_images/math/fbef32139b4a057413537424ce7fa88d2e7f9ed6.png) .
.
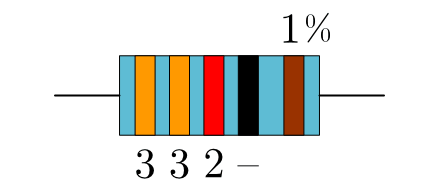
Der Zahlenwert
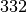 des Widerstands hat drei von Null verschiedene
Zahlenziffern; somit muss es sich um einen Metallschicht-Widerstand mit
fünf Ringen handeln. Die ersten beiden Ziffern des Zahlenwertes sind
jeweils
des Widerstands hat drei von Null verschiedene
Zahlenziffern; somit muss es sich um einen Metallschicht-Widerstand mit
fünf Ringen handeln. Die ersten beiden Ziffern des Zahlenwertes sind
jeweils 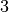 ; somit müssen die ersten beiden Farbringe orange sein.
Die dritte Ziffer ist
; somit müssen die ersten beiden Farbringe orange sein.
Die dritte Ziffer ist 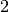 ; somit muss der dritte Farbring rot sein.
Es muss keine Null angehängt werden, somit ist der vierte Farbring schwarz.
; somit muss der dritte Farbring rot sein.
Es muss keine Null angehängt werden, somit ist der vierte Farbring schwarz.Der fünfte Farbring ist ohne Angabe eines Toleranzbereiches nicht festgelegt. (Metallschicht-Widerstände haben üblicherweise einen Toleranzbereich von
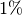 oder geringer.)
oder geringer.)
Der Widerstand hat fünf Ringe, somit geben die ersten drei Ziffern den Zahlenwert und die vierte Ziffer den Multiplikator bzw. die Anzahl an Nullen an.
Der erste Ring ist braun, somit ist die erste Ziffer des Widerstandswertes gleich
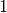 . Der zweite Ring ist grün, somit ist die zweite Ziffer des
Widerstandswertes gleich
. Der zweite Ring ist grün, somit ist die zweite Ziffer des
Widerstandswertes gleich 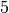 . Der dritte Ring ist schwarz, somit ist
die dritte Ziffer des Widerstandswertes gleich
. Der dritte Ring ist schwarz, somit ist
die dritte Ziffer des Widerstandswertes gleich 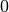 . Der vierte Ring
ist orange, somit sind drei Nullen an den Zahlenwert anzuhängen. Insgesamt
ergibt sich somit ein Widerstandswert von
. Der vierte Ring
ist orange, somit sind drei Nullen an den Zahlenwert anzuhängen. Insgesamt
ergibt sich somit ein Widerstandswert von ![\unit[150\,000]{\Omega} =
\unit[150]{k \Omega}](../_images/math/3c649652cdff94236e4b1025224da9e6ec342e34.png) .
.Der fünfte Ring ist violett, somit liegt der Toleranzbereich bei
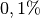 . Der tatsächliche Wert des Widerstands liegt somit
zwischen
. Der tatsächliche Wert des Widerstands liegt somit
zwischen ![\unit[95]{k \Omega}](../_images/math/ab0d1a9d243d76806970a003af1c85905b6547d7.png) und
und ![\unit[105]{k \Omega}](../_images/math/e6d40189a9882fb9ed16285bd5ffc985ce985c47.png) .
.
Kondensatoren¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Kondensatoren.
Für die im Kondensator gespeicherte Ladung
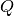 gilt:
gilt:![Q = C \cdot U = \unit[100 \cdot 10^{-6}]{F} \cdot \unit[9,0]{V} = \unit[0,9 \cdot 10^{-3}]{Q}](../_images/math/9b061f85d5591d978c87ae129db8bd11256676c1.png)
Die Einheit ergibt sich aus der Beziehung
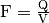 . Im Kondensator ist somit eine Ladung von knapp einem
Mili-Coulomb gespeichert.
. Im Kondensator ist somit eine Ladung von knapp einem
Mili-Coulomb gespeichert.Für die gespeicherte Energiemenge
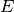 gilt:
gilt:![E = \frac{1}{2} \cdot C \cdot U^2 = \frac{1}{2} \cdot \unit[100 \cdot
10^{-6}]{F} \cdot \left( \unit[9,0]{V} \right)^2 \approx \unit[0,004]{J}](../_images/math/ec8a4b0aa782a2c1bb8d9d4505b9e5053be05756.png)
Die Einheit ergibt sich aus folgender Beziehung:
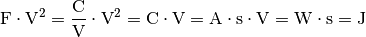
Im Kondenator sind somit rund
![\unit[4]{mJ}](../_images/math/579f4f7ce105d017e463ab477c9182b1678a9347.png) an Energie gespeichert.
an Energie gespeichert.
Für den zeitlichen Spannungsverlauf während des Ladevorgangs gilt für Kondensatoren:
![U_{\mathrm{C}} &= U \cdot \left(1 - e^{-\frac{t}{\tau}}\right) \\[4pt]
&= U - U \cdot e^{-\frac{t}{\tau}}](../_images/math/0dd609bfd6d303a96a823d22663d1d3f6c8eddc3.png)
Um die Gleichung zu lösen, müssen zunächst die Terme sortiert werden:
![U \cdot e^{-\frac{t}{\tau}} &= U - U_{\mathrm{C}} \\[6pt]
e^{-\frac{t}{\tau}} &= \frac{U - U_{\mathrm{C}}}{U}](../_images/math/44426745a0b9987755dcd5cc6989332bae0a73dd.png)
Nun können beide Seiten der Gleichung logarithmiert werden. Man erhält:
![-\frac{t}{\tau} &= \phantom{-}\ln{\left( \frac{U - U_{\mathrm{C}}}{U} \right)} \\[4pt]
\Rightarrow t &= - \ln{\left( \frac{U - U_{\mathrm{C}}}{U} \right)} \cdot \tau](../_images/math/186727c622a43ddd0291138ec3953aae9a4b5e94.png)
Durch ein Einsetzen der Werte erhält man:
![t(U_{\mathrm{C}} = \unit[3]{V}) &= - \ln{\left(
\frac{\unit[(9,0-3,0)]{V}}{\unit[9,0]{V}} \right)} \cdot \unit[10 \cdot
10^{3}]{\Omega} \cdot \unit[470 \cdot 10^{-6}]{F} \approx \unit[1,9]{s}
\\[6pt]
t(U_{\mathrm{C}} = \unit[6]{V}) &= - \ln{\left(
\frac{\unit[(9,0-6,0)]{V}}{\unit[9,0]{V}} \right)} \cdot \unit[10 \cdot
10^{3}]{\Omega} \cdot \unit[470 \cdot 10^{-6}]{F} \approx \unit[5,2]{s}
\\[6pt]](../_images/math/5d49c2f15b33c7111a8403482a8e395eb50ddc37.png)
Das negative Vorzeichen hebt sich durch die Multiplikation mit dem Logarithmus auf, da das Argument des Logarithmus kleiner als Eins ist und der Logarithmus somit als Ergebnis einen negativen Wert liefert.
Die Einheit ergibt sich aus folgender Beziehung:
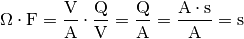
Es dauert also rund
![\unit[1,9]{s}](../_images/math/2b97467da39f0668e78f01ca8dffa051df69e2be.png) , bis der Kondensator auf
, bis der Kondensator auf
![\unit[3]{V}](../_images/math/bbb363d2c6e80babe898c73e95016fba9d64e015.png) und
und ![\unit[5,2]{s}](../_images/math/19a3053482abbef3f5e03b9c10c6d43fe0469be0.png) , bis der Kondensator auf
, bis der Kondensator auf
![\unit[6]{V}](../_images/math/96456f72a188a973330fe6e04ec5db948076876c.png) geladen ist.
geladen ist.Man kann nach dieser Rechenmethode somit auch indirekt bestimmen, wie lange der Kondensator für den Ladevorgang von
![\unit[3]{V}](../_images/math/bbb363d2c6e80babe898c73e95016fba9d64e015.png) bis
bis
![\unit[6]{V}](../_images/math/96456f72a188a973330fe6e04ec5db948076876c.png) benötigt, nämlich
benötigt, nämlich ![\unit[(5,2-1,9)]{s} \approx
\unit[3,3]{s}](../_images/math/841ded6e1af06dc18e46a824f4634de95f412460.png) .
.
Transformatoren¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Transformatoren.
Um die Windungszahl der Sekundärspule zu bestimmen, löst man die Transformator-Gleichung nach
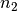 auf:
auf: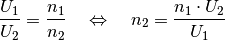
Eingesetzt ergibt sich mit
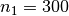 ,
, ![U_1 = \unit[230]{V}](../_images/math/76b9972207fe06d4e6f1234cc1dd0fe0ae40e2be.png) und
und
![U_2 = \unit[100]{V}](../_images/math/85af021a46e238014b9be51b93f5fd0a96a29f09.png) :
:![n_2 = \frac{n_1 \cdot U_2}{U_1} = \frac{300 \cdot
\unit[100]{V}}{\unit[230]{V}} \approx 130](../_images/math/1bb2d6b6aaade6c5114ec55f39fc59bc1a11ea94.png)
Die Sekundärspule muss somit
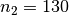 Windungen besitzen.
Windungen besitzen.
Die Windungszahlen stehen nach der Transformator-Gleichung
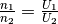 im gleichen Verhältnis wie die
anliegenden Spannungen. An der Spule mit der höheren Anzahl an Windungen liegt
daher auch stets die höhere Spannung, an der Spule mit der geringeren Anzahl
an Windungen die niedrigere Spannung an.
im gleichen Verhältnis wie die
anliegenden Spannungen. An der Spule mit der höheren Anzahl an Windungen liegt
daher auch stets die höhere Spannung, an der Spule mit der geringeren Anzahl
an Windungen die niedrigere Spannung an.
Um die Stromstärke in der Sekundärspule zu bestimmen, löst man die Transformator-Gleichung nach
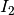 auf:
auf: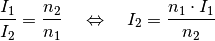
Eingesetzt ergibt sich mit
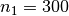 ,
, 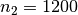 und
und
![I_1 = \unit[2]{A}](../_images/math/b568c410e4556282dd24916f7baf7e011f7b05ad.png) :
:![I_2 = \frac{n_1 \cdot I_1}{n_2} =
\frac{300 \cdot \unit[2]{A}}{1200} = \unit[0,5]{A}](../_images/math/2ef242042123b917187ceadf9977dc683605228e.png)
Die Stromstärke in der Sekundärspule des Transformators beträgt somit
![I_2 = \unit[0,5]{A}](../_images/math/3af723b4cf7616cbd2fc5d4c840dbdcac5ab5beb.png) .
.