Körpereigenschaften¶
Volumen¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Volumen.
Wird die Farbe gleichmäßig aufgetragen, so gilt für das zum Anstreichen einer Fläche
 mit einer Schichtdicke
mit einer Schichtdicke 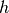 benötigte
Farbvolumen:
benötigte
Farbvolumen: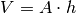
Umgekehrt kann aus dieser Formel die Dicke
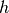 der Farbschicht
berechnet werden, wenn das Volumen
der Farbschicht
berechnet werden, wenn das Volumen  und die Fläche
und die Fläche  bekannt sind. Dazu muss nur berücksichtigt werden, dass ein Liter einem
Kubik-Dezimeter entspricht:
bekannt sind. Dazu muss nur berücksichtigt werden, dass ein Liter einem
Kubik-Dezimeter entspricht:![\unit[1]{l} \equiv \unit[1]{dm^3} = \unit[\frac{1}{1000} ]{m^3}](../_images/math/7e07902fd15e60e973c8859e8e39852e38913e55.png)
Somit gilt:
![h = \frac{V}{A} = \frac{\unit[\frac{1}{1000} ]{m^3}}{\unit[6]{m^2}}
\approx \unit[0,00017]{m} = \unit[0,17]{mm}](../_images/math/9b8107c449bf6d1c6d2e463727f795ba0e90a501.png)
Bei der Etikettenangabe wird somit davon ausgegangen, dass die Farbe mit einer Schichtdicke von knapp
![\unit[0,2]{mm}](../_images/math/0a9fded8c5a1a3c69e1bf4e62e2e8da3f5f2cd47.png) aufgetragen wird.
aufgetragen wird.
Die Fläche
 der (rechteckigen) Blechtafel ist gleich dem Produkt
aus ihrer Länge
der (rechteckigen) Blechtafel ist gleich dem Produkt
aus ihrer Länge  und Breite
und Breite 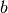 :
:![A = l \cdot b = \unit[1,50]{m} \cdot \unit[1,20]{m} = \unit[1,80]{m^2}](../_images/math/33d80872d9c4ed0d4e5d736601c2dad92c330610.png)
Das Volumen
 der nötigen Lackschicht kann damit als Produkt der
Fläche
der nötigen Lackschicht kann damit als Produkt der
Fläche  und der (gleichmäßigen) Schichtdicke
und der (gleichmäßigen) Schichtdicke ![h =
\unit[0,1]{mm} = \unit[0,000\,1]{m}](../_images/math/951586c3b274c388f1a22f930c5a86ca8132b099.png) berechnet werden:
berechnet werden:![V = A \cdot h = \unit[1,8]{m^2} \cdot \unit[0,000\,1]{m} =
\unit[0,000\,18]{m^3} = \unit[0,18]{dm^3}](../_images/math/b11dbf8a13191a545320eb172a05387069ca30b4.png)
Zum Streichen der Fläche mit der angegebenen Schichtdicke sind somit je Fläche rund
![\unit[0,2]{dm^3} = \unit[0,2]{l}](../_images/math/b17740a3a5ddec4e83328c6bcdd1e90545ae2916.png) nötig; für beide Seiten sind
entsprechend
nötig; für beide Seiten sind
entsprechend ![\unit[0,4]{l}](../_images/math/73390f6a5809a7424401bbd05c6bb5791e572889.png) Lack notwendig.
Lack notwendig.
Dichte¶
Die folgenden Lösungen beziehen sich auf die Übungsaufgaben zum Abschnitt Dichte.
In Kork und Styropor ist verhältnismäßig viel Luft eingelagert. Körper aus Kork oder Styropor nehmen daher bei einer bestimmten Masse
 ein großes
Volumen
ein großes
Volumen  ein. Die Dichte
ein. Die Dichte 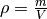 ist somit gering.
ist somit gering.
Die Formel für die Dichte
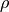 eines Körpers lautet
eines Körpers lautet 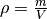 . Die Masse
. Die Masse  und das Volumen
und das Volumen  des Würfels
sind bekannt. Eingesetzt ergibt sich:
des Würfels
sind bekannt. Eingesetzt ergibt sich:![\rho = \frac{m}{V} = \frac{\unit[178]{g} }{\unit[20]{cm^3} } = 8,9
\unit[]{\frac{g}{cm^3} }](../_images/math/98739d7022019d26f00320380017cc9d3b6dc634.png)
Die Dichte des Würfels beträgt
![\unit[8,9]{g/cm^3}](../_images/math/bbf13ee6257533ad51f0acca687291d00f262d45.png) . Da Kupfer die gleiche
Dichte besitzt, handelt es sich wahrscheinlich um einen Würfel aus Kupfer.
. Da Kupfer die gleiche
Dichte besitzt, handelt es sich wahrscheinlich um einen Würfel aus Kupfer.
Eine mögliche Lösung besteht darin zu überlegen, dass Kubick-Dezimeter gerade einem Liter entspricht:
![\unit[1]{dm^3} = \unit[1]{l}](../_images/math/3f6f66c11e292684acf61e88a5524e3b3e610a5c.png)
Quecksilber hat eine Dichte von
![\unit[13,6]{kg/dm^3}](../_images/math/4668de498473781d3ffdacebf508ef419ab24f0e.png) , d.h. es passen
, d.h. es passen
![m = \unit[13,6]{kg}](../_images/math/320488f656a50bf827ab507d0619211f2f0494d8.png) in ein Volumen
in ein Volumen ![V = \unit[1]{l}](../_images/math/291b039306ee123afc4a103602232de0b4ec9fea.png) . Nun steht
in der
. Nun steht
in der 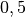 -Liter-Flasche nur die Hälfte dieses Volumens zur Verfügung,
so dass auch nur die Hälfte dieser Masse hinein passt – das sind
-Liter-Flasche nur die Hälfte dieses Volumens zur Verfügung,
so dass auch nur die Hälfte dieser Masse hinein passt – das sind
![\unit[6,8]{kg}](../_images/math/3fa245fc5aa7cf64769cb673980ee96d4ef90412.png) . Quecksilber der Masse
. Quecksilber der Masse ![m = \unit[6]{kg}](../_images/math/7a4a33a6a78abbe72a4c737b8c09898002c44f05.png) füllt
die Flasche somit nicht aus.
füllt
die Flasche somit nicht aus.Ein anderer Lösungsweg ergibt sich, indem man berechnet, welches Volumen die sechs Kilogramm Quecksilber einnehmen:
Aus der gegebenen Dichte
![\rho = \frac{m}{V} = \unit[13,6]{kg/dm^3}](../_images/math/cc00570233e266ecaab34b94c9e9ddd33e45733c.png) des Quecksilbers und seiner Masse
des Quecksilbers und seiner Masse ![m = \unit[6]{kg}](../_images/math/7a4a33a6a78abbe72a4c737b8c09898002c44f05.png) lässt sich das
Volumen des Quecksilbers bestimmen:
lässt sich das
Volumen des Quecksilbers bestimmen:
![V = \frac{m}{\rho } = \frac{\unit[6]{kg}}{ \unit[13,6]{{\frac{kg}{dm^3}}
}} = \unit[0,441]{dm^3} = \unit[0,441]{l}](../_images/math/d81eff1c84d873f6f36880a6f4c0e646ef640613.png)
Dieses Volumen ist kleiner als
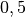 Liter, also kann man es in die
Flasche füllen.
Liter, also kann man es in die
Flasche füllen.
Würde Glaswolle ausschließlich aus dem Glasgemisch bestehen, so würde sich aus der Dichte
![\rho = \unit[2,5]{g/cm^3} = \unit[2500]{kg/m^3}](../_images/math/a95c7e07fc97878bada472926ce788083e5352eb.png) bei
einem Volumen von
bei
einem Volumen von ![V = \unit[1]{m^3}](../_images/math/8b42a139aae5d41c10c67ec42b1b1480d54ffcb5.png) eine Masse von
eine Masse von ![m =
\unit[2500]{kg}](../_images/math/e3aa323ab5c744fecf2a26c326dd8a745c88430b.png) ergeben:
ergeben:![\rho = \frac{m}{V} \quad \Leftrightarrow \quad m = \rho \cdot V \\
m = \unit[2500]{\frac{kg}{m^3} } \cdot \unit[1]{m^3} = \unit[2500]{kg}](../_images/math/f29f5f6ce0ea9061656d66bdd5497622c05a4560.png)
Tatsächlich wiegt ein Kubickmeter Glaswolle jedoch nur
![\unit[100]{kg}](../_images/math/be9452821f262a5e7d038160a6345abf15ebb36c.png) . Das Glasgemisch kann somit – das Gewicht der Luft
wird an dieser Stelle vernachlässigt – den entsprechenden Bruchteil des
Volumens ausmachen:
. Das Glasgemisch kann somit – das Gewicht der Luft
wird an dieser Stelle vernachlässigt – den entsprechenden Bruchteil des
Volumens ausmachen: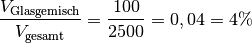
Der Anteil des Glasgemisches am Gesamtvolumen begrägt somit
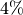 .
.
Das Volumen
![V = \unit[75,0]{cm^3}](../_images/math/02d92e23396f6ff101831fe6cfe1c530294c822e.png) an Wasser, das aus dem Überlaufgefäß
heraus fließt, entspricht dem Volumen des Holz-Blei-Klotzes.
an Wasser, das aus dem Überlaufgefäß
heraus fließt, entspricht dem Volumen des Holz-Blei-Klotzes.Das Bleistück mit der Masse
![m_{\mathrm{Pb}} = \unit[400]{g}](../_images/math/528e037a7344b8242d9f3ccba39b490de75e3b99.png) und der
Dichte
und der
Dichte ![\rho_{\mathrm{Pb}} = \unit[11,3]{g/cm^3}](../_images/math/ed0e7b75db1dbe470ae22d2de73a03862e0e402c.png) hat alleine folgendes
Volumen:
hat alleine folgendes
Volumen:![V_{\mathrm{Pb}} = \frac{m_{\mathrm{Pb}}}{V_{\mathrm{Pb}}} =
\frac{\unit[400]{g}}{\unit[11,3]{\frac{g}{cm^3} }} = \unit[35,4]{cm^3}](../_images/math/1a581853b477d282e9de42da0e495b15c1e2fd28.png)
Das restliche Volumen
![V - V_{\mathrm{Pb}} = \unit[75,0]{cm^3} -
\unit[35,4]{cm^3} = \unit[39,6]{cm^3}](../_images/math/d39b74e395f9047c490e9d536d4124b4fd1396a6.png) entspricht somit dem Volumen
entspricht somit dem Volumen 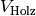 des Holzstücks. Da die Masse
des Holzstücks. Da die Masse ![m_{\mathrm{Holz}} =
\unit[27,5]{g}](../_images/math/69ca1d7113ed4a493d3a21d6e7abad46640cfcbf.png) des Holzstücks ebenfalls bekannt ist, kann seine Dichte durch
Einsetzen der Werte in die Dichte-Formel berechnet werden:
des Holzstücks ebenfalls bekannt ist, kann seine Dichte durch
Einsetzen der Werte in die Dichte-Formel berechnet werden:![\rho_{\mathrm{Holz}} = \frac{m_{\mathrm{Holz}}}{V_{\mathrm{Holz}}} =
\frac{\unit[27,5]{g}}{\unit[39,6]{cm^3}} \approx \unit[0,69]{\frac{g}{cm^3} }](../_images/math/7c4017e3d39b7d542ebd85181345a33fef9dc9be.png)
Bei der Holzprobe könnte es sich nach Tabelle Dichte einiger Festkörper somit um Buche handeln.
Das Volumen des Drahts (
![r = \unit[1,00]{mm} = \unit[0,10]{cm}](../_images/math/6ee462b864ec616663a7416ac83ee8012a102c9f.png) ;
;
![l = \unit[100]{m} = \unit[10\,000]{cm}](../_images/math/32c2356f94f11ac9df496eae135da4a48ea032fb.png) ) kann mit Hilfe der
Volumen-Formel für zylindrische Körper berechnet werden:
) kann mit Hilfe der
Volumen-Formel für zylindrische Körper berechnet werden:![V_{\mathrm{Draht}} = \pi \cdot r^2 \cdot l = \pi \cdot \unit[0,01]{cm^2} \cdot
\unit[10\,000]{cm} \approx \unit[314]{cm^3}](../_images/math/b60cc0936ab061926c4a9ad8cf0d8c3dd2f0cb1b.png)
Die Masse des Kupferdrahts
![m_{\mathrm{Draht}} = V_{\mathrm{Draht}} \cdot
\rho_{\mathrm{Cu}} = \unit[314]{cm^3} \cdot \unit[8,9]{\frac{g}{cm^3}} =
\unit[2795]{g}](../_images/math/c58ec4bc1d59f0deec3202363a7ec4d8354d2791.png) beträgt somit rund
beträgt somit rund ![\unit[2,8]{kg}](../_images/math/00aba2e8bd7a1c88c01aeff3beb54e5802dcf8d1.png) .
.
Die Masse des Schnees ist gleich dem Produkt aus seinem Volumen und seiner Dichte:
![m = \rho \cdot V = \unit[200]{\frac{kg}{m^3}} \cdot (\unit[3,00]{m} \cdot
\unit[2,00]{m} \cdot \unit[0,25]{m}) = \unit[300]{kg}](../_images/math/0547a65fa7a9f80f4179930b11309f80340746da.png)
Die Schneelast hat somit eine Masse von
![\unit[300]{kg}](../_images/math/53103be27ad538f6f1fde72591cbe85ff5a84507.png) .
.
