Stromstärke, Spannung und Widerstand¶
Damit ein elektrischer Strom durch einen Körper fließen kann, müssen zwei Bedingungen erfüllt sein:
- In ihm müssen frei bewegliche Ladungsträger (beispielsweise Elektronen) vorhanden sein.
- An ihm muss eine elektrische Spannung (Ladungsdifferenz) anliegen.
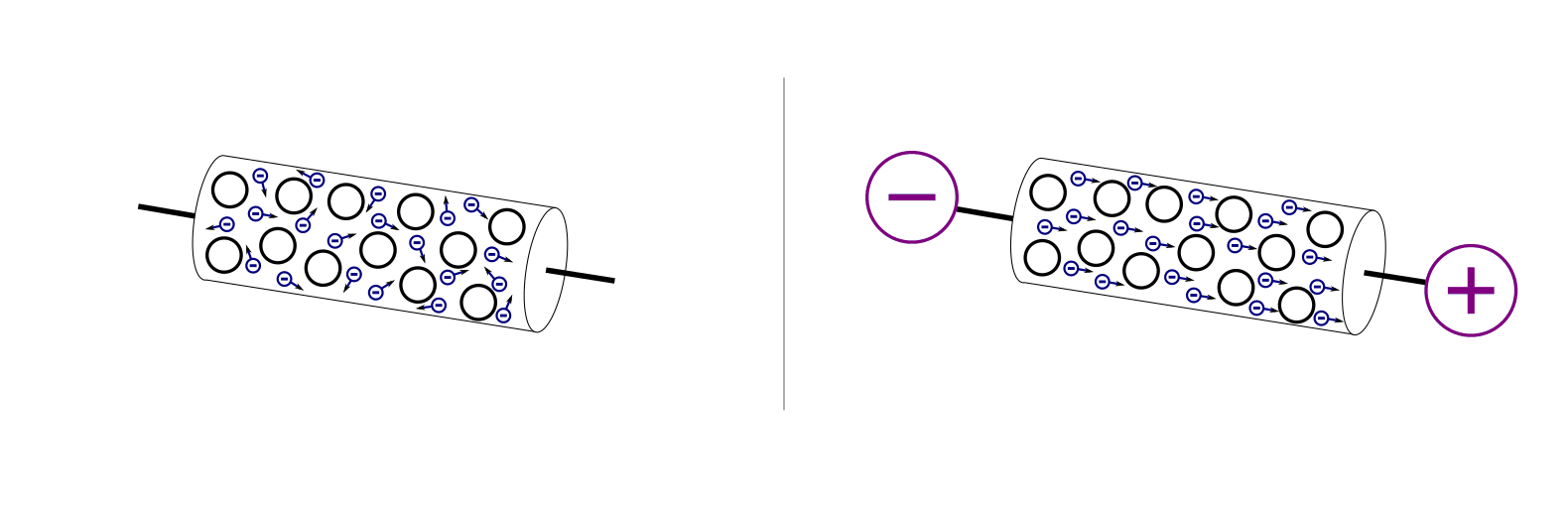
Durch das Anlegen einer elektrischen Spannung wird aus einer ungeordneten Elektronenbewegung („Wärmebewegung“) ein geordneter Elektronenstrom.
Modell:
Ähnlich wie Wasser durch eine Pumpe in Bewegung versetzt werden kann, lassen sich Elektronen durch Stromquellen („Elektronenpumpen“) in Bewegung versetzen.
Während Wasser mit einer Wasserpumpe in eine Wasserleitung gepresst wird, erzeugt eine Stromquelle (Batterie oder Generator) an einem ihrer Pole eine erhöhte Konzentration an Elektronen und damit eine elektrische Spannung.
Die Stromstärke¶
Ein elektrischer Strom tritt auf, wenn sich elektrische Ladungen bewegen. Die elektrische Stromstärke ist ein Maß dafür, welche Menge an elektrischer Ladung in einer bestimmten Zeit durch einen Körper fließt.
Modell:
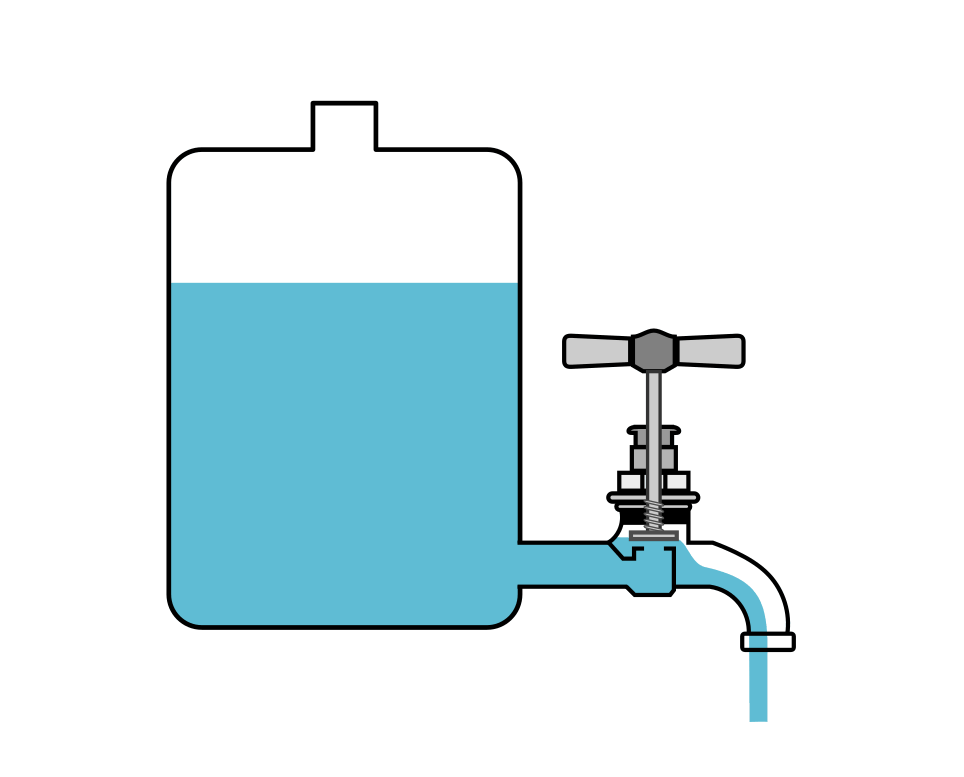
Wird ein Wasserhahn aufgedreht, so beginnt Wasser zu fließen. Umso weiter der Wasserhahn aufgedreht wird, desto mehr Wasser strömt in einer bestimmten Zeit aus ihm heraus. Diese Kenngröße könnten wir als „Wasserstromstärke“ bezeichnen.
Entsprechend führt die geordnete Bewegung von elektrischen Ladungen zu einem elektrischen Stromfluss: Umso mehr Elektronen (oder Ionen) ein Leiterstück in einer bestimmten Zeit durchlaufen, desto höher ist die auftretende elektrische Stromstärke. So wie die maximale Wassermenge, die in einer Wasserleitung fließen kann, von dem Durchmesser des Wasserrohres abhängt, so kann in einem dickeren Stromleiter ein stärkerer Strom fließen als in einem dünnen.
Definition:
Die elektrische Stromstärkeist gleich der Menge an elektrischer Ladung
, die in einer Zeitspanne
transportiert wird:
(1)¶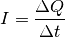
Einheit:
Die elektrische Stromstärke wird in Ampereangegeben. Eine Stromstärke von 1 Ampere bedeutet, dass an jeder Stelle im Leiter je Sekunde 1 Coulomb an Ladung (etwa 6 Trillionen Elektronen!) transportiert wird.
| Elektronisches Gerät | Stromstärke in Ampere |
| Elektrische Armbanduhr | 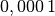 |
| Glimmlampe, Kopfhörer | 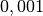 |
| Industrielle Sensoren | 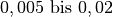 |
| Glühbirne | 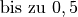 |
| Bügeleisen | 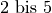 |
| Elektrischer Ofen | 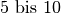 |
| Elektrisches Schweißen | 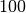 |
| Straßenbahnmotor | 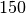 |
| Überlandleitung | 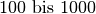 |
| Elektro-Lokomotive | 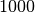 |
| Aluminium-Schmelzofen | 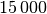 |
| Blitz | 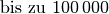 |
Physikalische und technische Stromrichtung
Die Bewegung von Ladungsträgern konnte erstmals in elektrisch leitenden Flüssigkeiten („Elektrolyten“) in Form von positiv geladenen Ionen beobachtet werden. Anhand dieser historischen Entdeckung wurde die Stromrichtung als diejenige Richtung festgelegt, entlang der sich positiv geladene Ladungsträger in einem Leiter bewegen: Sie gehen stets vom Plus-Pol einer Stromquelle aus und bewegen sich in Richtung Minus-Pol.
Diese Konvention wurde beibehalten, obwohl man später feststellte, dass in leitenden Festkörpern vor allem die Bewegung der negativ geladenen Elektronen von entscheidender Bedeutung für den Stromfluss ist. Da diese vom Minus-Pol ausgehen und sich sich in Richtung Plus-Pol bewegen, muss man stets zwischen der ursprünglich festgelegten („technischen“) und der tatsächlichen („physikalischen“) Bewegungsrichtung der geladenen Teilchen unterscheiden:
- Die „technische“ Stromrichtung verläuft stets von Plus nach Minus.
- Die „physikalische“ Stromrichtung gibt die tatsächliche Bewegungsrichtung der geladenen Teilchen an. Für positive Ladungsträger ist sie mit der technischen Stromrichtung identisch, für negative Ladungsträger zeigt sie in die entgegengesetzte Richtung.
In der heutigen Elektronik wird stets die technische Stromrichtung als Norm für Schaltpläne und Beschriftungen verwendet. Auch wenn der Ladungstransport durch Elektronen erfolgt, so sagt man, dass der Strom „von Plus nach Minus“ fließe. Dies mag physikalisch unkorrekt sein; entscheidend ist allerdings vielmehr, dass von der Polung abhängige Bauteile (beispielsweise Dioden und Transistoren) immer nach dem gleichen Schema hergestellt werden.[1]
Stromdichte
Neben der Stromstärke  wird in der Elektrotechnik bisweilen auch mit
der so genannten Stromdichte
wird in der Elektrotechnik bisweilen auch mit
der so genannten Stromdichte 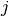 gerechnet. Diese ergibt sich, wenn man
die Stromstärke
gerechnet. Diese ergibt sich, wenn man
die Stromstärke  durch die Querschnittsfläche
durch die Querschnittsfläche  des Leiters
dividiert:
des Leiters
dividiert:
(2)¶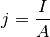
Als Einheit für die Stromdichte wählt man üblicherweise aufgrund der gängigen
Leiter-Querschnitte 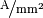 . Mittels der Stromdichte kann
beispielsweise erklärt werden, weshalb der Draht in einer Glühbirne leuchtet,
nicht jedoch die Zuleitungen: Obwohl die Stromstärke gleich ist, ist in dem
wesentlich dünneren Draht im Inneren der Glühbirne die Stromdichte und somit
auch die Wärme-Entwicklung höher.
. Mittels der Stromdichte kann
beispielsweise erklärt werden, weshalb der Draht in einer Glühbirne leuchtet,
nicht jedoch die Zuleitungen: Obwohl die Stromstärke gleich ist, ist in dem
wesentlich dünneren Draht im Inneren der Glühbirne die Stromdichte und somit
auch die Wärme-Entwicklung höher.
Die elektrische Spannung¶
Elektrischer Strom fließt nicht von selbst, sondern benötigt eine elektrische Spannung als Ursache. Elektrische Spannung wiederum ist das Ergebnis einer Ladungstrennung, beispielsweise einer Erhöhung der Konzentration an Elektronen an einer Stelle gegenüber einer anderen Stelle.
Modell:
In einem Wassertank hängt der Druck, der auf den Wasserhahn ausgeübt wird, ausschließlich von der Füllhöhe im Tank ab: Umso höher der Behälter gefüllt wurde, desto höher ist der Wasserdruck am unteren Ende.
Entsprechend ist für das Fließen eines elektrischen Stromes eine gezielte Anhäufung von elektrischer Ladung notwendig. Umso stärker die Elektronen an einer Stelle verdichtet werden, also je mehr Arbeit bei der Ladungstrennung investiert wird, desto steiler ist das Konzentrationsgefälle an elektrischer Ladung und damit die elektrische Spannung.
Definition:
Die elektrische Spannungist gleich der Menge an Arbeit
, die bei der Ladungstrennung auf eine Ladungsmenge
aufgewendet wird:
(3)¶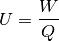
Einheit:
Die elektrische Spannung wird in Voltangegeben. Eine Spannung von
bedeutet, dass für je
an Ladung eine Arbeit von
zur Ladungstrennung aufgewendet wird.
| Elektronisches Gerät | Spannung in Volt |
| Zink-Kohle-Batterie (je Zelle) | 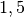 |
| Fahrrad-Dynamo | 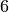 |
| Autobatterie | 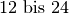 |
| Netzspannung | 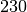 |
| Drehstrom | 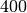 |
| Generator in Kraftwerk | 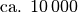 |
| Hochspannung | 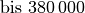 |
| Blitz | 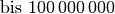 |
Das elektrische Potential
Die Spannung ist keine absolute Größe, man kann also streng genommen nicht angeben, wie groß die Spannung an einer bestimmten Stelle ist. Spannung bezieht sich vielmehr stets auf zwei Punkte: Man kann mit einem Spannungswert also nur angeben, wie groß die Spannung zwischen zwei Punkten ist. Gemäß der technischen Konvention, dass Strom stets „von Plus nach Minus“ fließt, kann die Spannungsdifferenz zwischen zwei Punkten als Maß dafür angesehen werden, wie stark und in welche Richtung der Strom vom einen Punkt zum anderen fließen möchte.
Um dennoch einen Absolutwert für die Menge einer Ladungsanhäufung angeben zu
können, hat man daher den Begriff „elektrisches Potential“ 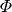 eingeführt. Das elektrische Potential ist vergleichbar mit der Höhe eines
Punktes über dem Meeresspiegel. Ein solcher Wert kann tatsächlich für jeden
einzelnen Punkt angegeben werden. Vergleicht man dann zwei verschiedene Punkte
hinsichtlich ihrer elektrischen Potentiale, so kann die Differenz
eingeführt. Das elektrische Potential ist vergleichbar mit der Höhe eines
Punktes über dem Meeresspiegel. Ein solcher Wert kann tatsächlich für jeden
einzelnen Punkt angegeben werden. Vergleicht man dann zwei verschiedene Punkte
hinsichtlich ihrer elektrischen Potentiale, so kann die Differenz 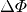 dieser Potentiale als elektrische Spannung
dieser Potentiale als elektrische Spannung  zwischen den
beiden Punkten aufgefasst werden:
zwischen den
beiden Punkten aufgefasst werden:
(4)¶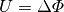
Im alltäglichen Sprachgebrauch werden trotz dieses Unterschieds die Begriffe Spannung und elektrisches Potential häufig als gleichwertig verwendet. Der Grund dafür liegt darin, dass als Bezugspunkt („Masse“, „Ground“, „Nullpotential“) für das elektrische Potential häufig der Minus-Anschluss der Stromquelle verwendet wird und dieser willkürlich den Wert Null erhält. Gegenüber diesem Bezugspunkt ist das elektrische Potential eines Punktes mit dem Spannungswert identisch. Haben hingegen zwei Punkte (beispielsweise in einer elektronischen Schaltung) jeweils von Null verschiedene elektrische Potentiale, so ist nur die Differenz der jeweiligen elektrischen Potentiale (umgangssprachlich: „Spannungsdifferenz“) als Ursache für einen Stromfluss von Bedeutung.
Die Gleichspannung¶
Eine elektrische Gleichspannung entsteht, wenn durch eine Stromquelle an einer Stelle ein Überschuss an elektrischer Ladung erzeugt wird. Wird der Stromkreis geschlossen, so strömen die frei beweglichen Elektronen im Leiter von der Stelle mit der höheren zu der Stelle mit der niedrigeren Ladungskonzentration, um einen Ladungsausgleich zu bewirken.
Eine zeitlich konstante Gleichspannung bewirkt in einem Leiter einen zeitlich konstanten Strom („Gleichstrom“).[2] Es wird allerdings auch dann von einer Gleichspannung gesprochen, wenn sie im zeitlichen Verlauf zwar unterschiedlich große Werte annimmt, dabei jedoch stets die gleiche Polung beibehält. Das Resultat ist in diesem Fall ein so genannter „pulsierender Gleichstrom“.
Die Wechselspannung¶
Manche elektrische Generatoren, beispielsweise Fahrrad-Dynamos, bewirken einen Strom, der einmal „von rechts nach links“, dann wieder „von links nach rechts“ fließt.[3] Die Ursache dafür ist eine Spannung, die ihre Richtung (beziehungsweise ihr Vorzeichen) regelmäßig wechselt und daher als Wechselspannung bezeichnet wird.
Die bekannteste Wechselspannung ist die sinusförmige Spannung des Stromnetzes,
die periodisch zwischen ![\unit[+325]{V}](../_images/math/71cc4c68fc661358f252ae6070c841fc8a3c3ba5.png) und
und ![\unit[-325]{V}](../_images/math/9f312f899fa7211648a71962f72942e6fd136721.png) hin
und her wechselt. Aufgrund der Schwankungen kann jedoch nur soviel elektrische
Leistung umgesetzt werden wie bei einer Gleichspannung von
hin
und her wechselt. Aufgrund der Schwankungen kann jedoch nur soviel elektrische
Leistung umgesetzt werden wie bei einer Gleichspannung von ![U_{\mathrm{eff}}
= \unit[230]{V}](../_images/math/e267ca3a416c9a9d55c78196ad8ac6918ce93df6.png) .[4] Diese so genannte „effektive Spannung“ einer
sinusförmigen Wechselspannung lässt sich allgemein nach folgender Formel
berechnen:[5]
.[4] Diese so genannte „effektive Spannung“ einer
sinusförmigen Wechselspannung lässt sich allgemein nach folgender Formel
berechnen:[5]
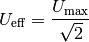
Die Frequenz der Wechselspannung im Stromnetz beträgt ![f=\unit[50]{Hz}](../_images/math/b0567bc00e22a176d35afbec4b2a54b40da38b09.png) ;
in einer Sekunde durchläuft die Wechselspannung also
;
in einer Sekunde durchläuft die Wechselspannung also 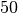 Perioden.
Hieraus ergibt sich eine Schwingungsdauer von
Perioden.
Hieraus ergibt sich eine Schwingungsdauer von ![T = \unit[\frac{1}{50}]{s}
= \unit[0,02]{s}](../_images/math/db4c6566d63c8b0bd4d5b0a0782ed53a1508a703.png) .
.
Der Vorteil einer Wechselspannung gegenüber einer (zeitlich konstanten) Gleichspannung liegt darin, dass sich der Wert der Wechselspannung mittels eines passenden Transformators leicht auf einen anderen beliebigen Spannungswert einstellen lässt.
Der elektrische Widerstand¶
In einem idealen elektrischen Leiter können sich die Ladungsträger völlig frei bewegen. In einem reellen Leiter hingegen treten stets Wechselwirkungen zwischen den sich bewegenden Elektronen und den zurückbleibenden Atomrümpfen auf. Ähnlich wie bei der mechanischen Reibung wird dabei elektrische Energie in Wärmeenergie umgewandelt (siehe auch Abschnitt Wärmeentwicklung in elektrischen Bauteilen).
Bei schlechten Leitern (beispielsweise Eisen) ist die Wechselwirkung zwischen Elektronen und Atomen stärker als bei guten Leitern (beispielsweise Kupfer). Zum einen erwärmen sich schlechte Leiter dadurch schneller als gute Leiter, zum anderen muss an ihnen eine höhere elektrische Spannung angelegt werden, um den gleichen Stromfluss zu erreichen.
Definition:
Unter dem elektrischen Widerstandeines Stromkreises versteht man das Verhältnis aus der Spannung
zwischen den Enden eines Leiters und der Stärke des Stromes
im Leiter:
(5)¶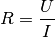
In gleicher Form lässt sich auch der elektrische Widerstand einzelner Bauteile angegeben.
Einheit:
Der elektrische Widerstand wird in Ohmangegeben. Ein elektrischer Widerstand von
bedeutet, dass eine Spannung von
aufgewendet werden muss, um eine Stromstärke von
zu erreichen:
![\unit[1]{Ohm} = \unit[1]{\frac{Volt}{Ampere}}](../_images/math/feaf6733b5cddf94f2f056bc14a4461b51527bb8.png)
Das Ohmsche Gesetz¶
Der Zusammenhang zwischen elektrischer Spannung, Stromstärke und Widerstand wurde im Jahr 1826 durch Georg Simon Ohm entdeckt. Ihm zu Ehren wird auch heute noch die Widerstandsgleichung (5) als „Ohmsches Gesetz“ bezeichnet und in folgender Form angegeben:
(6)¶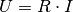
Das Ohmsche Gesetz (6) ist in seiner Gültigkeit auf homogene Materialien begrenzt. In zahlreichen Fällen kann es dennoch, beispielsweise bei Reihen- und Parallelschaltungen, beim Ermitteln von Spannungen oder Stromstärken helfen, wenn die jeweiligen elektrischen Widerstände bekannt sind.
Neben den beiden bisher genannten Formen (5) und (6) kann der Zusammenhang zwischen Stromstärke und Spannung auch folgendermaßen angegeben werden:[6]
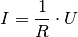
Bei einer höheren Spannung ist somit auch die Stromstärke höher, die durch einen
Stromkreis oder ein elektronisches Bauteil fließt. Die entsprechende Kennlinie
entspricht, wie in Abbildung Ohmsches Gesetz zu erkennen ist, einer Geraden, die umso steiler
verläuft, desto niedriger der Widerstandswert 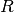 ist.
ist.
In der Elektronik bezeichnet man Bauteile, die zumindestens näherungsweise diese Charakteristik erfüllen, ebenfalls als Widerstände.
Nicht-Ohmsche Widerstände
In Halbleiter-Bauteilen (z.B. Dioden, Transistoren, usw.) ist der Zusammenhang zwischen Stromstärke und Spannung nicht linear; vielmehr ist in diesen Bauteile erst ab einer bestimmten Spannung ein Stromfluss möglich, der bei einer weiteren Erhöhung der Spannung überproportional ansteigt (Abbildung Kennlinie einer Diode in Durchlass-Richtung).
Das Ohmsche Gesetz kann in solchen Fällen (näherungsweise) genutzt werden, wenn die Widerstandswerte in Abhängigkeit von der Stromstärke oder Spannung bekannt sind, also als Diagramm oder in tabellarischer Form für bestimmte Werte vorliegen.
Der spezifische Widerstand¶
Unterschiedliche Stoffe leiten den Strom unterschiedlich gut, sie besitzen also
einen unterschiedlichen spezifischen Widerstand 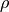 . Je kleiner der
spezifische Widerstand eines Materials ist, desto besser leitet es den
elektrischen Strom.[7]
. Je kleiner der
spezifische Widerstand eines Materials ist, desto besser leitet es den
elektrischen Strom.[7]
Definition:
Bei einem Körper aus homogenem Stoff, beispielsweise einem Metalldraht, hängt der Widerstand bei einer bestimmten Temperatur vom Material, von seiner Längeund von seiner Querschnittsfläche („Dicke“)
ab. Es gilt:
(7)¶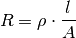
Einheit:
Aus der Definition (7) ergibt sich für den spezifischen Widerstand
die Einheit
.
Da die meisten Bauteile und Leitungen eine wesentlich geringere Querschnittsfläche als
besitzen, ist auch folgende Einheit üblich:
Beispiele:
Ein
![l = \unit[1]{m}](../_images/math/69420c8193f16687c0a23a04c73647c5ecd12c52.png) langer Kupferdraht
langer Kupferdraht ![(\rho_{\mathrm{Cu}} =
\unit[0,0156]{\Omega \cdot \frac{mm^2}{m} } )](../_images/math/db696504de3fb82b1539e4c5a59b12f4152f3bc7.png) mit einer Querschnittsfläche
von
mit einer Querschnittsfläche
von ![\unit[1]{mm^2}](../_images/math/3b94ab243756d45de8e0729ff7f9fc7d95505a7f.png) hat einen elektrischen Widerstand von
hat einen elektrischen Widerstand von![R = \rho_{\mathrm{Cu}} \cdot \frac{l}{A} = \unit[0,0156]{\Omega \cdot
\frac{mm^2}{m} } \cdot \frac{\unit[1]{m}}{\unit[1]{mm^2}} =
\unit[0,0156]{\Omega }](../_images/math/a211431d6d13286219540faa16572d4b46629b62.png)
Würde man den Drahtdurchmesser um den Faktor
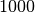 von
von
![\unit[1]{mm}](../_images/math/d96fa97c6d890bf9efd0b11602b0de8767afb6d5.png) auf
auf ![\unit[1]{m}](../_images/math/51a34f0de982f7a3c2dd6c9b85685eb17b0f71f0.png) erhöhen, so ergäbe sich eine
um
erhöhen, so ergäbe sich eine
um 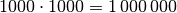 größere Querschnittsfläche und
damit ein um eine Million geringerer elektrischer Widerstand.
größere Querschnittsfläche und
damit ein um eine Million geringerer elektrischer Widerstand.Ein
![\unit[4]{mm^2}](../_images/math/32480bebb4ff5ef4e346140f09b328a348dd869a.png) dicker und
dicker und ![\unit[30]{mm} = \unit[0,03]{m}](../_images/math/986fe0e3b38002ab49ff8f4c0cf96def799935f3.png) langer Stab aus Edelstahl
langer Stab aus Edelstahl ![(\rho_{\mathrm{V2A}} = \unit[0,720]{\Omega
\cdot \frac{mm^2}{m} })](../_images/math/2c53f390bef297b5547734e9077f19cfc7446814.png) hat einen elektrischen Widerstand von
hat einen elektrischen Widerstand von![R = \rho_{\mathrm{V2A}} \cdot \frac{l}{A} = \unit[0,720]{\Omega \cdot
\frac{mm^2}{m} } \cdot \frac{\unit[0,03]{m}}{\unit[4]{mm^2}} =
\unit[0,0054]{\Omega }](../_images/math/632c265b7367c9b412da8ef16f161591f83033a0.png)
| Kupfer | ![\unit[0,0156]{\Omega }](../_images/math/1b35c5758c575273f069a7b927664562fc9cf276.png) |
| Silber | ![\unit[0,0151]{\Omega }](../_images/math/6b8708197adc4f503cde27dcef2d1ad72422b61a.png) |
| Gold | ![\unit[0,0204]{\Omega }](../_images/math/f2f7fc46edf533d582a874f804b5779983a294b2.png) |
| Aluminium | ![\unit[0,0265]{\Omega }](../_images/math/d7ed31c4ada89d2738eec9d17ca7bdaf7955048c.png) |
| Messing | ![\unit[0,070]{\Omega }](../_images/math/fe981dcb57a704d3f1df3ca79a75daca550eb948.png) |
| Konstantan | ![\unit[0,5]{\Omega }](../_images/math/87a5db19adc84fc96eae8b45b3e990c97a07eb28.png) |
| Edelstahl (V2A) | ![\unit[0,720]{\Omega }](../_images/math/53f0f8488e84784ce54b4e0b17ff87f473d025e8.png) |
| Eisen | ca. ![\unit[1,25]{\Omega }](../_images/math/a0cfd772541538930ac545eda8abc01b16e90db4.png) |
Da sich die spezifischen Widerstände von verschiedenen Stoffen erheblich voneinander unterscheiden, lassen sich die Materialien in elektrische Leiter, Halbleiter und Isolatoren einteilen.
Temperaturabhängigkeit des spezifischen Widerstands
Bei metallischen Leitern hängt der spezifische Widerstand 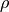 über
einen weiten Temperaturbereich linear von der Temperatur ab:
über
einen weiten Temperaturbereich linear von der Temperatur ab:
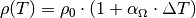
Hierbei bezeichnet man 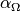 als
Temperaturkoeffizient von Ohmschen Widerständen. Für Metalle ist
als
Temperaturkoeffizient von Ohmschen Widerständen. Für Metalle ist
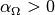 , der spezifische Widerstand nimmt somit mit
steigender Temperatur zu. Halbleiter hingegen werden mit zunehmenden
Temperaturen besser leitfähig, bei tiefen Temperaturen hingegen werden sie
zunehmend zu Isolatoren.
, der spezifische Widerstand nimmt somit mit
steigender Temperatur zu. Halbleiter hingegen werden mit zunehmenden
Temperaturen besser leitfähig, bei tiefen Temperaturen hingegen werden sie
zunehmend zu Isolatoren.
Anmerkung:
| [1] | Auch beim Autoverkehr ist weniger entscheidend, ob ein Links- oder ein Rechtsverkehr vorherrscht, sondern vielmehr, dass sich alle Verkehrsteilnehmer an die gleichen Grundregeln halten.. ;-) |
| [2] | Im englischen Sprachbereich wird Gleichstrom als „direct current“ (DC) bezeichnet. |
| [3] | Im englischen Sprachbereich wird Wechselstrom als „alternating current“ (AC) bezeichnet. |
| [4] | Diese Werte gelten für das europäische Stromnetz. In Nordamerika
beispielsweise beträgt die Effektivspannung im Stromnetz
![\unit[120]{V}](../_images/math/16230f650519204cce1bcd1b76352ba5ba0f2cb5.png) bei einer Netzfrequenz von bei einer Netzfrequenz von ![\unit[60]{Hz}](../_images/math/8839f0712d7b0da80985ecc030103cf6c2ad8a6a.png) . . |
| [5] | Da 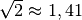 ist, kann man sich als praktische
Faustregel merken, dass der Spitzenwert einer Wechselspannung stets um
das ist, kann man sich als praktische
Faustregel merken, dass der Spitzenwert einer Wechselspannung stets um
das 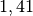 -fache höher liegt als ihr Effektivwert. -fache höher liegt als ihr Effektivwert. |
| [6] | Der Kehrwert
Der elektrische Leitwert wird in der Einheit „Siemens“ (Kurzzeichen
|
| [7] | Der Kehrwert
Die elektrische Leitfähigkeit wird meist in der Einheit |
Hinweis
Zu diesem Abschnitt gibt es Experimente und Übungsaufgaben.



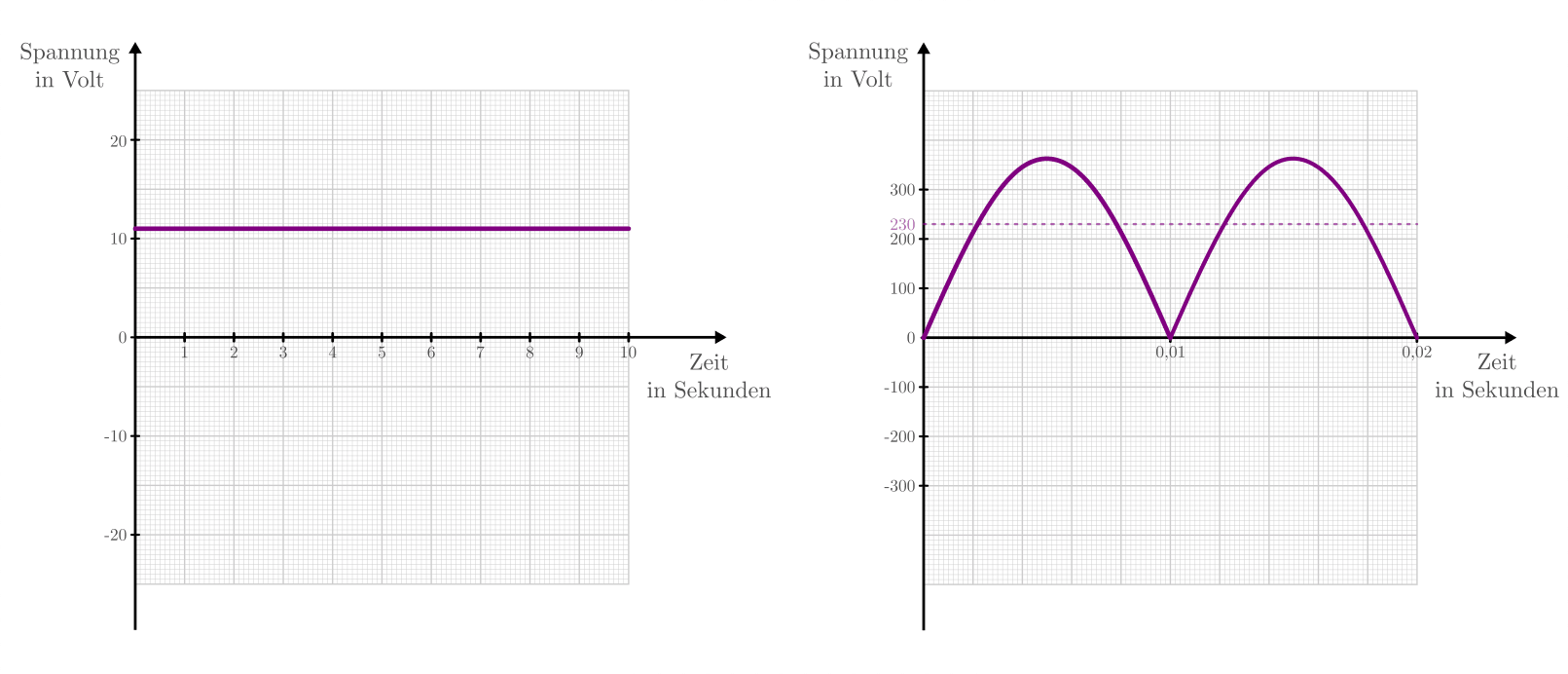
![\unit[12]{V}](../_images/math/200aaa6e051ac61dbd160817b12948222f584232.png) -Gleichspannung und einer
„pulsierenden“
-Gleichspannung und einer
„pulsierenden“ ![\unit[230]{V}](../_images/math/e3c789febd54eb564f08c8ecbf6b7b2274acf1c4.png) -Gleichspannung.
-Gleichspannung.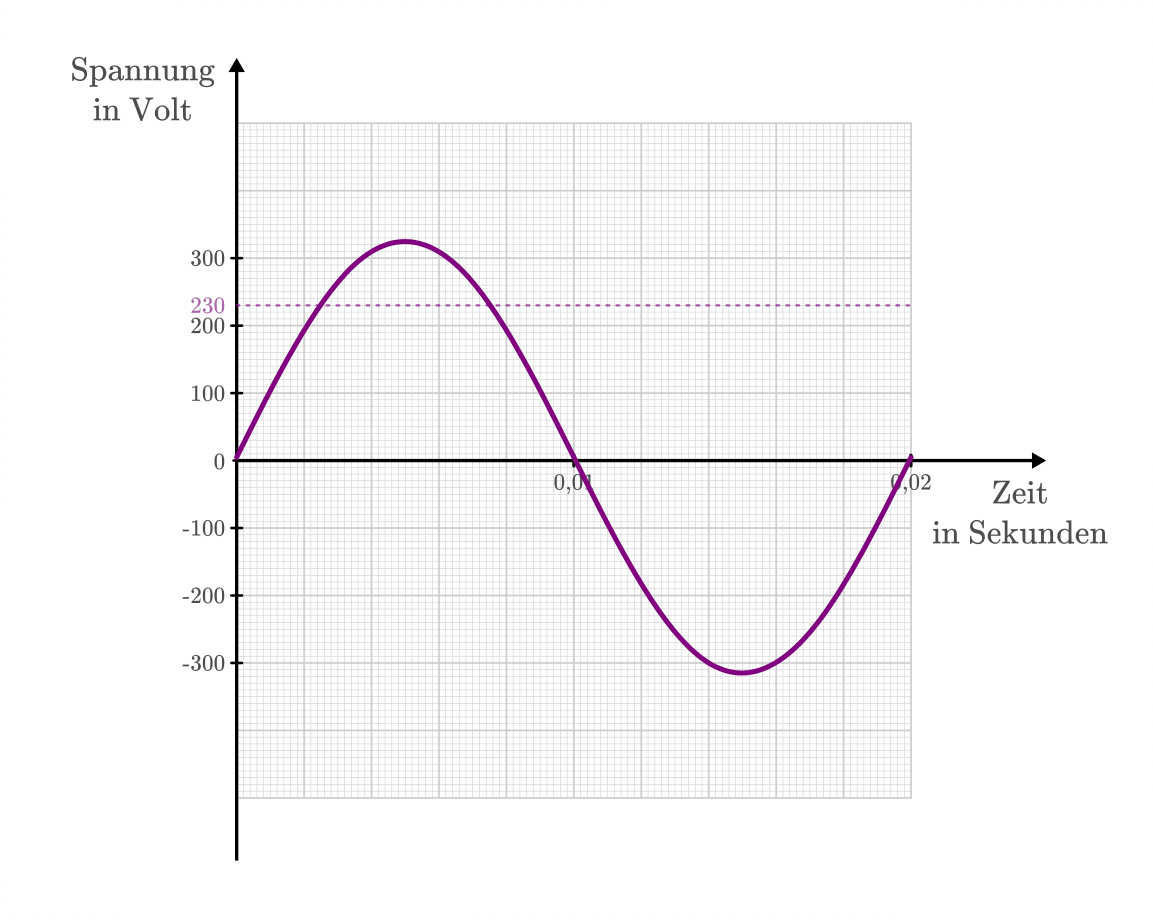
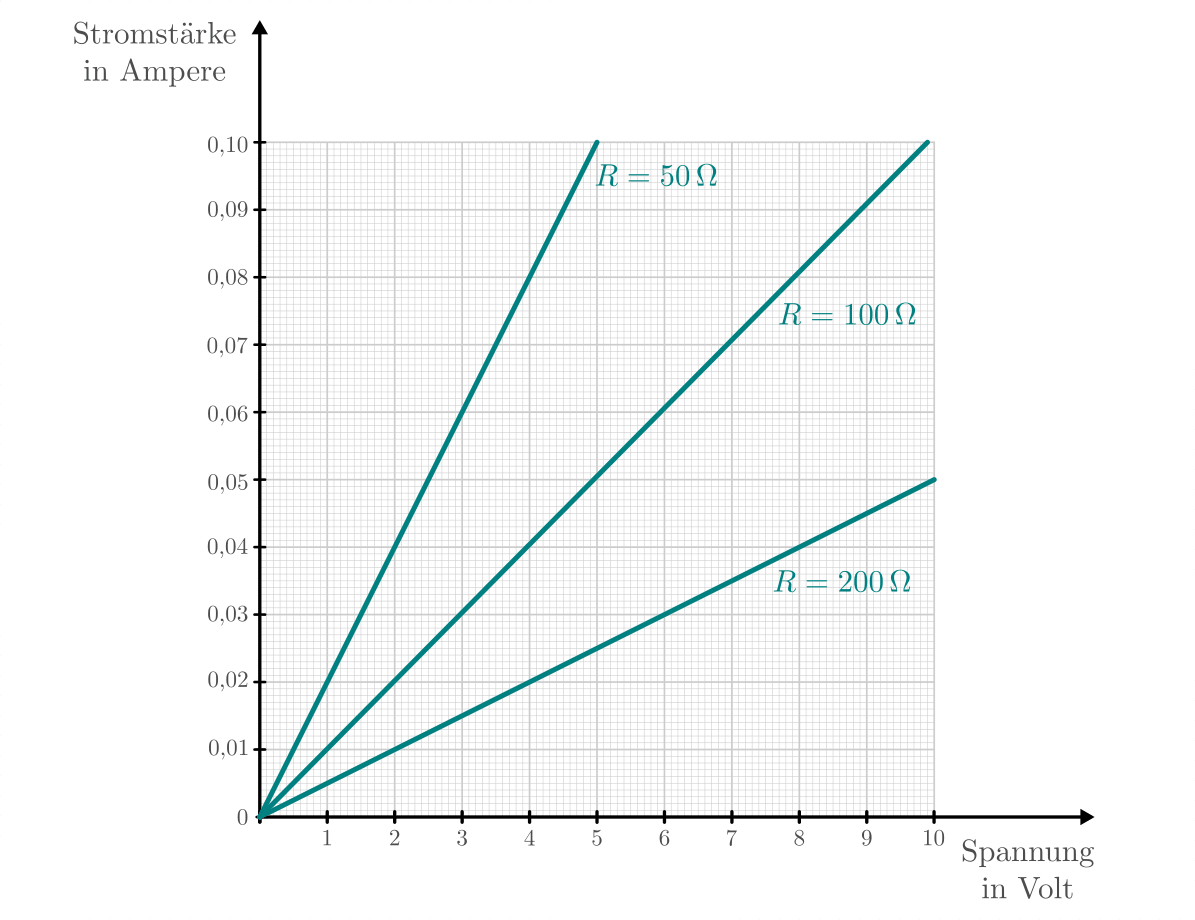
![\unit[1]{\Omega \cdot \frac{mm^2}{m} } = \unit[10^{-6}]{\Omega \cdot
\frac{m^2}{m} } = \unit[10^{-6}]{\Omega \cdot m}](../_images/math/33173a30cca78c87ba8ac8eec9225d21ac134858.png)
![(l\!=\!\unit[1]{m}](../_images/math/9f963b09cf1628f6958e9d778317fd0de7e5a444.png) ,
,
![A\!=\!\unit[1]{mm^2})](../_images/math/293b0289a7fedbe662804c98b167861c8df5e52f.png)
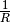 wird bisweilen auch als „elektrischer
Leitwert“
wird bisweilen auch als „elektrischer
Leitwert“ 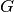 bezeichnet:
bezeichnet: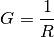
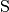 ) angegeben, wobei
) angegeben, wobei ![\unit[1]{S} =
\unit[1]{\frac{1}{\Omega}} = \unit[1]{\frac{A}{V}}](../_images/math/48dc4a1cdde95adf34564ff0105d4edeebc6dc72.png) gilt. Je größer der
elektrische Leitwert eines Stromkreises ist, desto größer ist die
Stromstärke bei gleicher anliegender Spannung.
gilt. Je größer der
elektrische Leitwert eines Stromkreises ist, desto größer ist die
Stromstärke bei gleicher anliegender Spannung.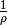 wird auch als „elektrische
Leitfähigkeit“
wird auch als „elektrische
Leitfähigkeit“  bezeichnet:
bezeichnet: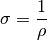
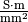 angegeben. Je größer die elektrische Leitfähigkeit eines
Materials ist, desto geringer ist sein elektrischer Widerstand bei gleicher
Querschnittsfläche und Länge.
angegeben. Je größer die elektrische Leitfähigkeit eines
Materials ist, desto geringer ist sein elektrischer Widerstand bei gleicher
Querschnittsfläche und Länge.