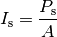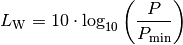Eigenschaften von Schall¶
Als „Schall“ bezeichnen wir alle Klänge, Geräusche usw. die Menschen und/oder Tiere mit ihrem Gehör wahrnehmen können. Damit Schall entstehen kann, muss ein mechanischer Körper in einen entsprechenden Schwingungszustand gebracht werden.
Schallquellen und Ausbreitung von Schall¶
Als Schallquelle wird ein Körper bezeichnet, der durch mechanische Schwingung Schall erzeugt. Dabei handelt es sich meist um einen elastischen Festkörper, doch auch Flüssigkeiten und Gase können als Schallquellen auftreten.
Beispiele:
- Saiteninstrumente (beispielsweise Gitarren oder Violinen), gespannte Gummis (beispielsweise von Trommeln) und ähnliche elastische Festkörper erzeugen beim Anzupfen oder Anschlagen verschiedenartige Töne und Geräusche.
- Bewegte Flüssigkeiten verursachen Strömungsgeräusche („Plätschern“, „Rauschen“, usw).
- In Blasinstrumenten (beispielsweise Flöten) kann die darin enthaltene Luftmenge durch Anblasen in Schwingung versetzt werden. Hierdurch entstehen Klänge, die charakteristisch sind für die Größe, die Form und das Material des Instruments.
Bei einem Schallempfänger handelt es sich ebenfalls um einen elastischen Körper, der zu mechanischen Schwingungen angeregt werden kann und dabei die empfangenen Schallwellen in biologische oder elektrische Signale umsetzt.
Schall braucht stets eine stoffliche Substanz (akustisches „Medium“), um sich ausbreiten zu können. In einem Raum ohne Materie („Vakuum“) ist keine Schallausbreitung möglich.
Die Schallgeschwindigkeit
Bei der Schallausbreitung gehen mechanische Wellen kreisförmig von einer Schallquelle aus. Aus mikroskopischer Sichtweise werden dabei die Schwingungen der einzelnen Teilchen der Schallquelle durch Stoßvorgänge auf benachbarte Teilchen des akustischen Mediums übertragen. Auch innerhalb eines akustischen Mediums werden die Schwingungen der Teilchen durch Stoßvorgänge an benachbarte Teilchen weitergegeben.
| Material | Schallgeschwindigkeit in ![\unit[]{\frac{m}{s}}](../_images/math/f83291ca1b41bde4435330efa38b23dcbd8c6cac.png) |
| Gummi | 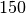 |
Luft (bei ![\unit[0]{\degree C}](../_images/math/e8140660503109a1fb799efbf73f7c53ebdd405d.png) ) ) |
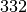 |
| Kork | 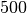 |
| Wasser | 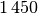 |
| Hartgummi | 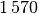 |
| Eis | 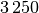 |
| Holz (Buche) | 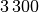 |
| Holz (Eiche) | 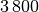 |
| Aluminium | 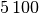 |
| Stahl | 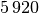 |
| Marmor | 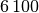 |
| Diamant | 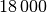 |
Die Ausbreitungsgeschwindigkeit der Schwingungszustände und damit auch der Schallwellen ist allgemein umso höher, je größer die Steifigkeit des Schall übertragenden Materials ist.[1]
Die Schallfrequenz
Je höher die Frequenz ist, mit der eine Schallquelle schwingt, desto höher
klingt der Ton, den sie erzeugt. Für Menschen hörbare Frequenzen liegen dabei in
einem Frequenzbereich von etwa ![\unit[15]{Hz}](../_images/math/e4fcead388020f90c0ee9eddaddcb31ba2146b91.png) bis
bis ![\unit[20]{kHz}](../_images/math/db4b1a43d004af08e2e75499105cb98714bbe03d.png) .
Die obere Grenze („Hörschwelle“) nimmt allerdings mit zunehmendem Alter deutlich
ab, d.h. ältere Menschen können hohe Töne deutlich schlechter hören, teilweise
sogar überhaupt nicht mehr.
.
Die obere Grenze („Hörschwelle“) nimmt allerdings mit zunehmendem Alter deutlich
ab, d.h. ältere Menschen können hohe Töne deutlich schlechter hören, teilweise
sogar überhaupt nicht mehr.
Der Frequenzbereich bis ![\unit[15]{Hz}](../_images/math/e4fcead388020f90c0ee9eddaddcb31ba2146b91.png) wird als Infraschall, der Bereich
von etwa
wird als Infraschall, der Bereich
von etwa ![\unit[20]{kHz}](../_images/math/db4b1a43d004af08e2e75499105cb98714bbe03d.png) bis
bis ![\unit[10]{GHz}](../_images/math/bd88689a4ed6a8fb2e43ce7164db69c266acc5cc.png) als Ultraschall
bezeichnet. Viele Tierarten verständigen sich im Ultraschallbereich,
beispielsweise Nachtfalter, Fledermäuse und Delfine (bei Frequenzen von
als Ultraschall
bezeichnet. Viele Tierarten verständigen sich im Ultraschallbereich,
beispielsweise Nachtfalter, Fledermäuse und Delfine (bei Frequenzen von
![\unit[100 \text{ bis } 200]{kHz}](../_images/math/903d66ab7bad802797a281953a9b47ec5f186912.png) ).
).
Technisch wird Ultraschall in vielerlei Anwendungen genutzt, beispielsweise in Entfernungsmessern und Bewegungsmeldern. In der Medizin lassen sich mittels Ultraschall schwacher Intensität Gewebeuntersuchungen durchführen; mit Ultraschall hoher Intensität können auch Geräte gereinigt sowie mineralische Ablagerungen im Körper (insbesondere Zahnstein, Blasen- und Nierensteine) zertrümmert werden.
Die Länge von Schallwellen
Mit kurzen Schritten und einer hohen Schrittfrequenz kann man sich genauso
schnell fortbewegen wie mit langen Schritten und einer niedrigen
Schrittfrequenz. Für Schallwellen gilt dieses Prinzip ebenso, denn tiefe wie
auch hohe Töne breiten sich gleichermaßen mit der Schallgeschwindigkeit
 aus.
aus.
Mathematisch lässt sich dieser Sachverhalt dadurch beschreiben, dass das Produkt
aus der Wellenlänge 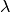 des Schalls (Einheit:
des Schalls (Einheit: ![\unit[]{m}](../_images/math/a143878c03956b162e29e5d8853979f4aa14b4f0.png) )
und der Schallfrequenz
)
und der Schallfrequenz 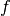 (Einheit:
(Einheit: ![\unit[]{\frac{1}{s}}](../_images/math/e6765f555796e269cd900e3fcf273988d0356c1a.png) ) gleich
der Schallgeschwindigkeit
) gleich
der Schallgeschwindigkeit  (Einheit:
(Einheit: ![\unit[]{\frac{m}{s}}](../_images/math/f83291ca1b41bde4435330efa38b23dcbd8c6cac.png) ) ist:
) ist:
(1)¶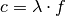
Durch Umstellen der obigen Formel kann unmittelbar die Länge einer Schallwelle
bei einer bestimmten Frequenz berechnet werden. Dabei wird genutzt, dass die
Schallgeschwindigkeit  eine Konstante ist, deren Wert nur vom Material
des akustischen Mediums abhängt (siehe Tabelle Schallgeschwindigkeiten in
verschiedenen Materialien). Entsprechend gilt:
eine Konstante ist, deren Wert nur vom Material
des akustischen Mediums abhängt (siehe Tabelle Schallgeschwindigkeiten in
verschiedenen Materialien). Entsprechend gilt:
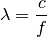
Je höher die Frequenz einer Schallwelle, desto kürzer ist somit ihre Wellenlänge.
Töne, Klänge und Geräusche¶
Schallwellen lassen sich in folgende drei Arten unterteilen:
Töne:
Als Ton bezeichnet man eine harmonische Schwingung, d.h. eine regelmäßige Sinusschwingung mit fester Frequenz. Verschiedene Töne lassen sich ihrer Frequenz beziehungsweise Tonhöhe nach anordnen. Beispielsweise besteht eine Tonleiter aus acht Tönen (Oktave) mit bestimmten Frequenzverhältnissen, wobei der letzte Ton der Oktave eine genau doppelt so hohe Frequenz besitzt wie der erste Ton der Oktave.
Zur Stimmung von Instrumenten wird häufig der so genannte „Kammerton“
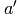 mit einer Frequenz von
mit einer Frequenz von ![\unit[440]{Hz}](../_images/math/8809363d37a85f0cc3380dae185300f663936f54.png) genutzt.
genutzt.Klänge:
Ein Klang setzt sich aus mehreren Tönen zusammen. Er entsteht durch Überlagerung verschiedener Frequenzen, die ganzzahlige Vielfache des tiefsten Tons („Grundtons“) sind.
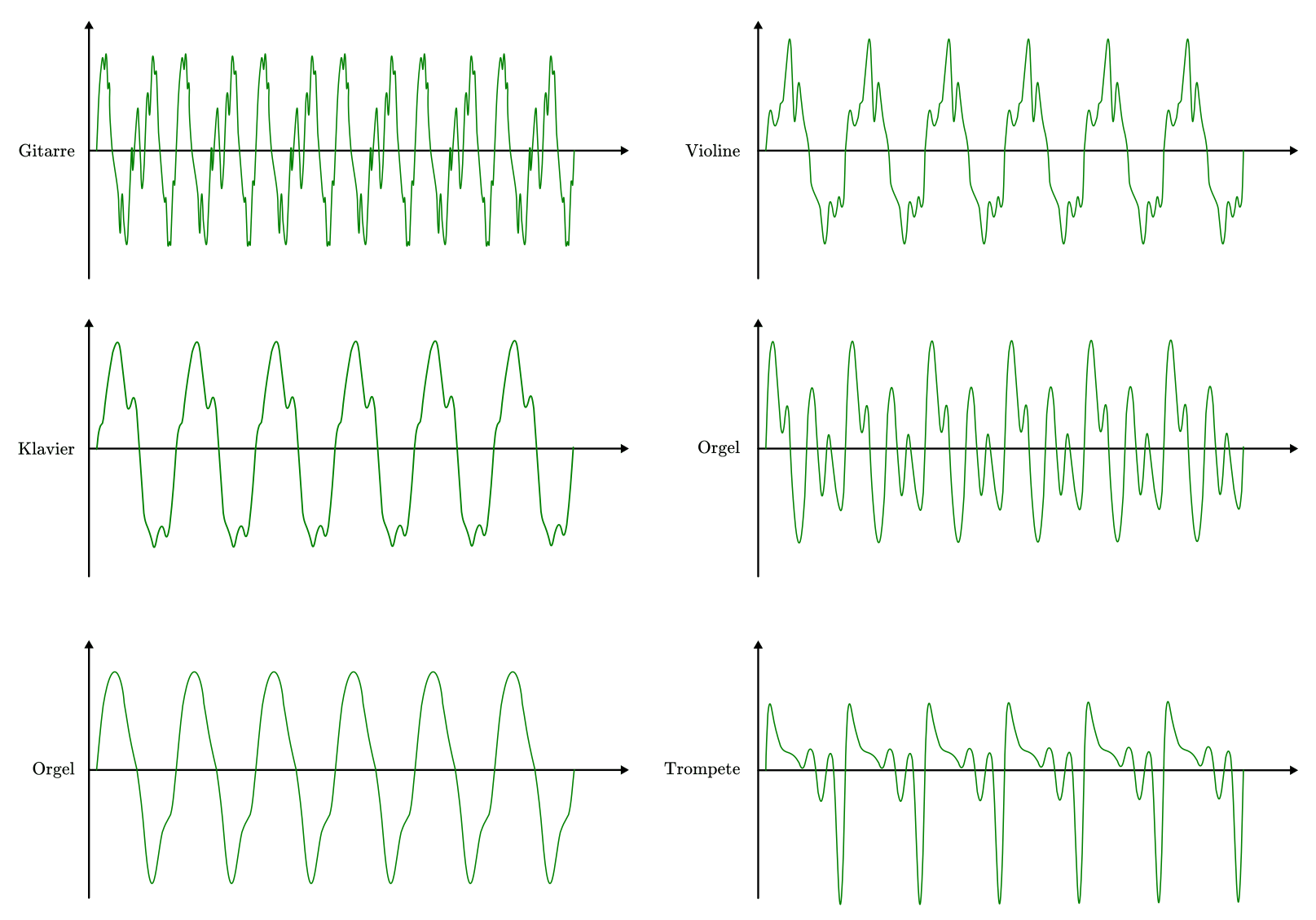
Die für jeden Gegenstand und jedes Musikinstrument typischen Vielfachen der Grundtonfrequenz werden „Obertöne“ genannt und sorgen für die charakteristischen „Klangfarben“ verschiedener Instrumente. Beispielsweise klingen eine Violine und ein Klavier deutlich unterschiedlich, auch wenn beide „gestimmt“ sind und auf beiden Instrumenten der gleiche Grundton gespielt wird.[2][3]
Anzumerken ist, dass die Klangmuster der dargestellten Instrumente selbst keinesfalls „regelmäßig“ sind: Alleine bei einen einzelnen gespielten Ton
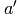 finden je Sekunde
finden je Sekunde 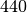 volle
Schwingungsvorgänge statt, von denen jeder einzelne etwas unterschiedlich
aussieht.
volle
Schwingungsvorgänge statt, von denen jeder einzelne etwas unterschiedlich
aussieht.Geräusche:
Geräusche setzen sich ebenfalls aus mehreren Tönen zusammen; allerdings überwiegen dabei „chaotische“, d.h. nicht periodische Schwingungsmuster. Bei einem ‚Knall‘ ist dies ebenfalls der Fall, mit dem Unterschied, dass die Lautstärke des Geräusches dabei sehr rasch abnimmt.
Schallintensität und Schallpegel¶
Als mechanische Welle überträgt Schall zwar keine Materie, aber Energie. Der
Energiefluss je Zeit wird, entsprechend der Definition der mechanischen
Leistung, als Schall-Leistung 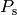 bezeichnet.
bezeichnet.
Definition:
Die Schallintensität
gibt an, wie groß die Schall-Leistung ist, die auf einer Fläche
auftrifft:
Die Schallintensität wird in der Einheit
angegeben.
Beispiel:
Ein in ein Gehäuse verbauter Lautsprecher sendet eine Schall-Leistung von
![P_{\mathrm{s}}=\unit[0,4]{W}](../_images/math/359974d211414dd99fe2aefbb5e57bd10192ae5a.png) aus. Wie groß ist die Schallintensität in
einer Entfernung von
aus. Wie groß ist die Schallintensität in
einer Entfernung von ![r=\unit[0,5]{m}](../_images/math/c5bb046d0d33d1b2f246f9ccab8bd5797d30c83d.png) vom Lautsprecher?
vom Lautsprecher?Lautsprecher erzeugen normalerweise kugelförmige Schallwellen. Ist der Lautsprecher in ein Gehäuse verbaut, so kann angenommen werden, dass er nur in die vor ihm liegende Raumhälfte Schall aussendet. Die gesamte Schall-Leistung von
![P_{\mathrm{s}}=\unit[0,4]{W}](../_images/math/359974d211414dd99fe2aefbb5e57bd10192ae5a.png) verteilt sich also auf immer größer
werdende Halbkugel-Flächen.
verteilt sich also auf immer größer
werdende Halbkugel-Flächen.Da die Oberfläche einer Kugel allgemein
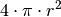 beträgt,
entspricht die Oberfläche einer Halbkugel
beträgt,
entspricht die Oberfläche einer Halbkugel 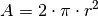 . Für
die Schallintensität
. Für
die Schallintensität 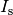 ergibt sich mit
ergibt sich mit
![r=\unit[0,5]{m}](../_images/math/c5bb046d0d33d1b2f246f9ccab8bd5797d30c83d.png) somit:
somit:![I = \frac{P_{\mathrm{s}}}{A} = \frac{\unit[0,4]{W}}{2 \cdot \pi \cdot
\left( \unit[0,5]{m} \right)^2} \approx \unit[0,25]{\frac{W}{m^2}}](../_images/math/f0c7d5c57ff3b605fc294e7c0579ff9462d64db4.png)
Wie man am obigen Beispiel sehen kann, nimmt die Schallintensität quadratisch
mit dem Abstand  von der Schallquelle ab, es ist also
von der Schallquelle ab, es ist also 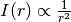 .
.
Die Schall-Leistung 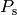 , die vom Ohr wahrgenommen wird, kann
wiederum mittels der Schallintensität
, die vom Ohr wahrgenommen wird, kann
wiederum mittels der Schallintensität 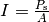 berechnet werden, indem man diese mit der Fläche
berechnet werden, indem man diese mit der Fläche  des Gehöreingangs
multipliziert; beim menschlichen Ohr beträgt die effektiv wirksame Fläche des
Trommelfells etwa
des Gehöreingangs
multipliziert; beim menschlichen Ohr beträgt die effektiv wirksame Fläche des
Trommelfells etwa ![\unit[55]{mm^2} = \unit[55 \cdot 10 ^{-6}]{m^2}](../_images/math/6037234020abe35f97dd0bfd6ffe9b54a087d2a4.png) .
.
Menschliche Ohren haben folgenden Wahrnehmungsbereich:
- Die minimale wahrnehmbare Schall-Leistung wurde bei Tests mit
unterschiedlichen Versuchspersonen als
![P_{\mathrm{min}} \approx \unit[1
\cdot 10 ^{-12}]{W}](../_images/math/d74ab9c2802e3cc7dcc982dc3e340203a0ba0191.png) ermittelt.
ermittelt. - Die maximale wahrnehmbare Schall-Leistung beträgt rund
![P_{\mathrm{max}}
\approx \unit[1]{W}](../_images/math/325f943a6091bf3a95d5010cf0055072adbb66cc.png) ; bei noch größeren Schall-Leistungen können Schmerzen und
irreparable Schäden auftreten.
; bei noch größeren Schall-Leistungen können Schmerzen und
irreparable Schäden auftreten.
Der große Wahrnehmungsbereich des menschlichen Ohres (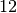 Größenordnungen!) hat dazu geführt, dass zur Messung der Lautstärke eine
logarithmische Skala eingeführt wurde, die nach
Alexander Graham Bell
benannt ist:
Größenordnungen!) hat dazu geführt, dass zur Messung der Lautstärke eine
logarithmische Skala eingeführt wurde, die nach
Alexander Graham Bell
benannt ist:
Definition:
Die Lautstärke von Schall kann anhand des so genannten Schall-Leistungs-Pegels gemessen, der folgendermaßen definiert ist:
Der Schall-Leistungs-Pegel hat keine Einheit; dennoch wird der sich ergebende Zahlenwert zur besseren Übersichtlichkeit mit Dezibel
bezeichnet.
Beispiele:
Welcher Schall-Leistungs-Pegel liegt vor, wenn die vom menschlichen Ohr empfangene Schall-Leistung den Wert
![P_{\mathrm{min}} = \unit[10
^{-12}]{W}](../_images/math/c211b4acde1eb0b3768dab19f79504c718f03d45.png) hat?
hat?Für
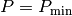 ergibt im Logarithmus der Wert
ergibt im Logarithmus der Wert 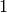 als
Argument. Da man jede Zahl mit
als
Argument. Da man jede Zahl mit 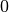 potenzieren muss, um den Wert
potenzieren muss, um den Wert
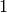 zu erhalten, ergibt der Logarithmus für diesen Wert den Wert
zu erhalten, ergibt der Logarithmus für diesen Wert den Wert
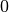 . Für die Lautstärke der empfangenen Schall-Leistung
. Für die Lautstärke der empfangenen Schall-Leistung
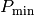 gilt somit:
gilt somit:![L_{\mathrm{W}} = 10 \cdot \log_{10}{\left(
\frac{P_{\mathrm{min}}}{P_{\mathrm{min}}} \right)} = 10 \cdot
\log_{10}{(1)} = 10 \cdot 0 = \unit[0]{dB}](../_images/math/7ecdfea8382ae6da6df050c15d1847177e9e2fb7.png)
Welcher Schall-Leistungs-Pegel liegt vor, wenn die vom menschlichen Ohr empfangene Schall-Leistung den Wert
![P_{\mathrm{max}} = \unit[1]{W}](../_images/math/7fce8b14baf81f9e4b800952e2f760ade76b21ef.png) hat?
hat?Für
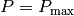 ergibt im Logarithmus der Wert
ergibt im Logarithmus der Wert
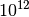 als Argument. Da man die Zahl
als Argument. Da man die Zahl 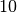 mit
mit 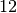 potenzieren muss, um den Wert
potenzieren muss, um den Wert 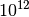 zu erhalten, ergibt der
Logarithmus für diesen Wert den Wert
zu erhalten, ergibt der
Logarithmus für diesen Wert den Wert 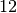 . Für die Lautstärke der
empfangenen Schall-Leistung
. Für die Lautstärke der
empfangenen Schall-Leistung 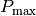 gilt somit:
gilt somit:![L_{\mathrm{W}} = 10 \cdot \log_{10}{\left(
\frac{P_{\mathrm{max}}}{P_{\mathrm{min}}} \right)} = 10 \cdot
\log_{10}{(10^{12})} = 10 \cdot 12 = \unit[120]{dB}](../_images/math/76ec6213722ee9252b89aff6397748e3fa0d0fe4.png)
Welcher Schall-Leistungs-Pegel wirkt auf ein menschliches Ohr, wenn es Schall von einem Lautsprecher mit einer Schall-Leistung von
![P_{\mathrm{s}}=\unit[0,4]{W}](../_images/math/359974d211414dd99fe2aefbb5e57bd10192ae5a.png) in einer Entfernung von
in einer Entfernung von
![r=\unit[0,5]{m}](../_images/math/c5bb046d0d33d1b2f246f9ccab8bd5797d30c83d.png) wahrnimmt?
wahrnimmt?Wie im obigen Beispiel gezeigt, hat die Schallintensität im Abstand von
![\unit[0,5]{m}](../_images/math/21dfa700d120099b5159ea50bb6d0d973c8fe8f0.png) den Wert
den Wert ![I = \unit[0,25]{\frac{W}{m^2}}](../_images/math/42fa1c8f83d205117559302a68dc4d64bb96ad5b.png) . Auf die
Fläche
. Auf die
Fläche ![A=\unit[55 \cdot 10^{-6}]{m^2}](../_images/math/1fcb9a0f30b4b09cbe77c47ca10f9b747a4e9e9c.png) des Trommelfells wirkt somit
folgende Schall-Leistung ein:
des Trommelfells wirkt somit
folgende Schall-Leistung ein:![P = I \cdot A = \unit[0,25]{\frac{W}{m^2}} \cdot \unit[55 \cdot
10^{-6}]{m^2} = \unit[1,375 \cdot 10^{-5}]{W}](../_images/math/8b6ed5e7ffc15ec69363f99fc361298990113c81.png)
Diese Schall-Leistung entspricht folgendem Schall-Leistungs-Pegel:
![L_{\mathrm{W}} = 10 \cdot \log_{10}{\left( \frac{P}{P_{\mathrm{min}}}
\right)} = 10 \cdot \log_{10}{\left(\frac{\unit[1,375 \cdot
10^{-5}]{W}}{\unit[1 \cdot 10^{-12}]{W}}\right)} = 10 \cdot
\log_{10}{(1,375 \cdot 10^{7})} \approx \unit[71,4]{dB}](../_images/math/dfd8abb549ee88222450158d7664dffba95799ec.png)
Die Schallpegel-Skala bildet also den normalen Hörbereich des Menschen auf einen
Zahlenbereich zwischen 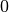 und
und 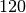 ab; Alltagsgeräusch haben
Schallpegel von etwa
ab; Alltagsgeräusch haben
Schallpegel von etwa ![\unit[30]{dB}](../_images/math/09a501dad5e0b8cf7ac4ec417e63f7279ed60d9e.png) bis
bis ![\unit[80]{dB}](../_images/math/df2316a43424cf9bab4ee6043eceb4504af40250.png) , ein
normales Gespräch erzeugt in
, ein
normales Gespräch erzeugt in ![\unit[1]{m}](../_images/math/51a34f0de982f7a3c2dd6c9b85685eb17b0f71f0.png) Entfernung einen Schallpegel
von circa
Entfernung einen Schallpegel
von circa ![\unit[60]{dB}](../_images/math/b6d7237dd01cea252a6a56e7d92e6445477a69a9.png) .
.
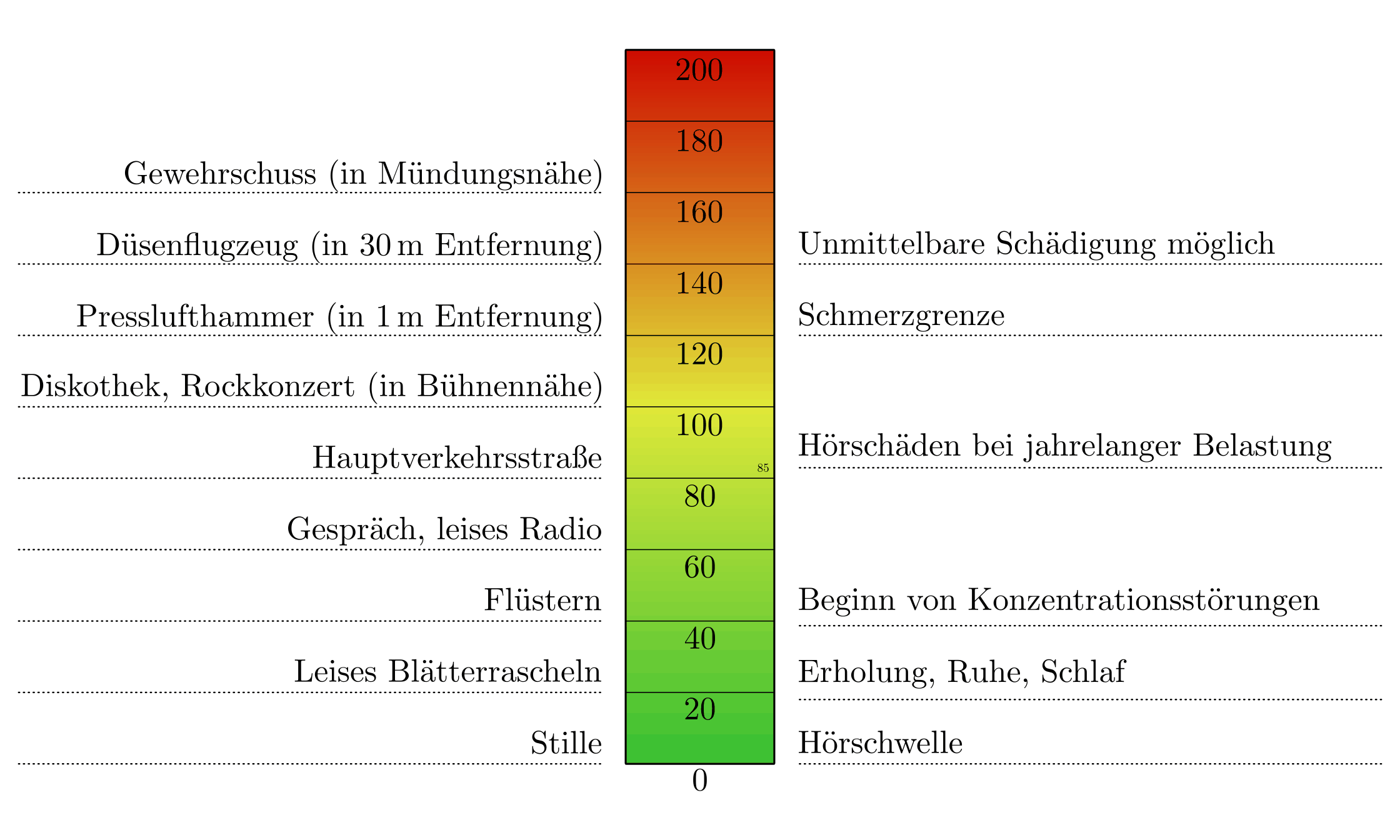
Schallpegel in Dezibel. Der Schallpegel hängt stets von der Entfernung zwischen der Schallquelle und dem Ohr beziehungsweise Messgerät ab.
Da es sich bei der Dezibel-Skala um eine logarithmische Skala handelt, bedeutet eine doppelte Leistung der Schallquelle keinesfalls auch eine Verdopplung des Dezibel-Werts. Vielmehr gilt in diesem Fall:
![P_2 = 2 \cdot P_1 \quad \Longleftrightarrow \quad
L_{\mathrm{W,2}} &= 10 \cdot \log_{10}{\left(
\frac{P_2}{P_{\mathrm{min}}} \right)} = 10 \cdot \log_{10}{\left(
\frac{2 \cdot P_1}{P_{\mathrm{min}}} \right)} \\[6pt] &= 10 \cdot \left(\log_{10}{\left(
\frac{P_1}{P_{\mathrm{min}}} \right)} + \log_{10}{(2)}\right) \\[6pt] &\approx 10 \cdot \left(
\log_{10}{\left( \frac{P_1}{P_{\mathrm{min}}} \right)} + \;\,0,301 \;\; \right) = L_{\mathrm{W_1}} + \unit[3,01]{dB}](../_images/math/893d33a799957a92c09e600a172dc867a1e64254.png)
Eine Verdoppelung der Leistung einer Schallquelle bewirkt also lediglich eine
Zunahme des Schallpegels um ![\Delta L_{\mathrm{W}} \approx
\unit[3,0]{dB}](../_images/math/6fd559704fb1a4ec6e413caabe3f01196054e3b9.png) . Ein derartiger Unterschied ist deutlich hörbar, kleinere
Schallpegel-Differenzen von nur
. Ein derartiger Unterschied ist deutlich hörbar, kleinere
Schallpegel-Differenzen von nur ![\unit[1]{dB}](../_images/math/1f0294700f14847dd34ea271c450b1afc4cf271f.png) bis
bis ![\unit[2]{db}](../_images/math/241df430261fec17dc88a8e45f41b43120306d34.png) sind meist nur bei direktem Vergleich erkennbar.
sind meist nur bei direktem Vergleich erkennbar.
Lautstärke bei unterschiedlichen Frequenzen
Mittels der Dezibel-Skala lassen sich die menschlich wahrgenommenen Lautstärken von Tönen nur dann vergleichen, wenn diese die gleiche Frequenz haben: Das menschliche Gehör reagiert nämlich auf unterschiedliche Schallfrequenzen unterschiedlich sensibel.
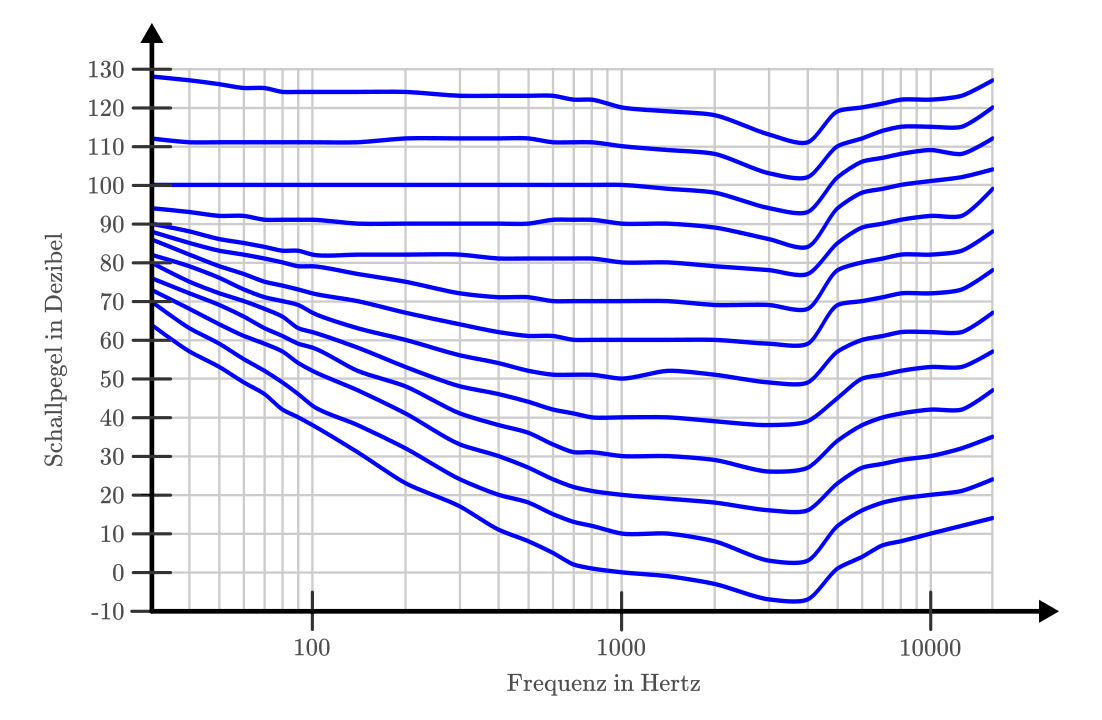
Die Richtwerte für die Dezibel-Skala wurden bei einer Schallfrequenz von
![f=\unit[1000]{Hz}](../_images/math/364e3df9f37f71c37041dad28e3946ec611f8e58.png) bestimmt. In der Abbildung Isophone
Lautstärkepegel stellt die unterste Kurve die
minimale Lautstärke dar, ab der Töne wargenommen werden können; bei
bestimmt. In der Abbildung Isophone
Lautstärkepegel stellt die unterste Kurve die
minimale Lautstärke dar, ab der Töne wargenommen werden können; bei
![f=\unit[1000]{Hz}](../_images/math/364e3df9f37f71c37041dad28e3946ec611f8e58.png) entspricht dies gerade dem Wert
entspricht dies gerade dem Wert
![L_{\mathrm{W}}=\unit[0]{dB}](../_images/math/289570a8f99c203743a5de913ee099da37640cbf.png) . Bei einem Frequenzwert von
. Bei einem Frequenzwert von
![f=\unit[400]{Hz}](../_images/math/9f7cb59c0f96984dd05b70028e53bd683700a96c.png) gibt die Kurve einen Wert von
gibt die Kurve einen Wert von ![L_{\mathrm{W}}
\approx \unit[10]{dB}](../_images/math/577a897a6d1a0fd8dbb84d3bf83a0b9a35046ab4.png) an, was bedeutet, dass bei dieser Frequenz der
Schallpegel um
an, was bedeutet, dass bei dieser Frequenz der
Schallpegel um ![\unit[+10]{dB}](../_images/math/de327de7de2a54f1ac3e02096040af4518ba3b11.png) höher sein muss, damit der Ton überhaupt
gehört werden kann – dies erfordert wiederum eine
höher sein muss, damit der Ton überhaupt
gehört werden kann – dies erfordert wiederum eine 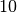 -fach höhere
Schall-Leistung
-fach höhere
Schall-Leistung 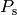 .
.
Dass Menschen Töne mit niedrigen Schallfrequenzen weniger intensiv wahrnehmen,
hat zur Folge, dass Basslautsprecher so konstruiert werden, dass sie hohe
Schall-Leistungen abstrahlen können; Hochton-Lautsprecher kommen entpsrechend
mit nur kleinen Schall-Leistungen aus. Am empfindlichsten ist das menschliche
Gehör bei Frequenzen im Bereich von ![\unit[3000]{Hz}](../_images/math/18b78702d075982a88c09ec942b5a2358d0e3be4.png) bis
bis
![\unit[4000]{Hz}](../_images/math/b6fcde19093612e39d9141992d8aa837631b4426.png) : In diesem Bereich genügen dem Ohr bereits empfangene
Leistungen von weniger als
: In diesem Bereich genügen dem Ohr bereits empfangene
Leistungen von weniger als ![P_{\mathrm{s}}=\unit[10^{-12}]{W}](../_images/math/1be02041ff388a4836d7bd3a4ff82f7eda2aedd0.png) , um Schall
wahrnehmen zu können.
, um Schall
wahrnehmen zu können.
Gibt man eine Lautstärke unter Berücksichtigung der in Abbildung Isophone Lautstärkepegel dargestellten Hörkurven an, so schreibt man dabei „Phon“ anstelle von „Dezibel“ als Einheit. Zu berücksichtigen ist dabei, dass es sich auch bei einer „Phon“-Angabe um einen reinen Zahlenwert handelt, der nur der Kenntlichkeit halber mit Phon benannt ist.
Anmerkungen:
| [1] | Bei einem gasförmigen akustischen Medium ist die
Schallgeschwindigkeit auch von Druck und Temperatur abhängig. Beispielsweise
beträgt die Schallgeschwindigkeit in ![\unit[0]{\degree C}](../_images/math/e8140660503109a1fb799efbf73f7c53ebdd405d.png) kalter Luft kalter Luft
![\unit[332]{\frac{m}{s}}](../_images/math/bf108139c10556d972b3e2a63c480b1e5ce952eb.png) , bei , bei ![\unit[20]{\degree C}](../_images/math/5306d44af8f7df91464b32ed64cda4ded46190b0.png) jedoch jedoch
![\unit[343]{m/s}](../_images/math/1cf43171efc5e44577700cbe3129f0ac03a020db.png) . . |
| [2] | Bei der Erstellung der in der Abbildung dargestellten Klangmuster wurden die Programme Musescore und Audacity verwendet:
|
| [3] | Im musikalischen Bereich wird üblicherweise nicht explizit auf die Obertöne eines Instruments eingegangen – stattdessen wird stets der jeweils gespielte Grundton als „Ton“ bezeichnet. Ein Klang, beispielsweise ein „Dreiklang“, setzt sich für einen Musiker entsprechend aus mehreren gleichzeitig klingenden (Grund-)Tönen zusammen und wird daher meist als Synonym für das Wort „Akkord“ genutzt. |