Atommodelle¶
Wohl schon immer faszinierten den Mensch die Frage, „was die Welt im Innersten zusammenhält“ (Goethe). Im Laufe der Geschichte haben einige Wissenschaftler und Philosophen hierzu einige Theorien entwickelt, um die Ergebnisse der stets neuen, technisch ausgefeilteren Experimente erklären zu können.
Im folgenden sind die heutiger Sicht wichtigsten dieser Atommodelle knapp zusammengefasst.
Das Demokrit-Modell¶
Das erste Atommodell geht auf die beiden griechischen Philosophen Leukipp und seinen Schüler Demokrit zurück. Beide waren der Ansicht, dass sich Materie nicht beliebig weit zerteilen lasse. Vielmehr müsse es ein kleinstes Teilchen geben, das nicht weiter zerteilbar ist: Das „Urkorn“ oder „Atom“ (atomos = griech. unteilbar).
Beide Philosophen stützten ihre Theorien nicht auf Experimente, sondern auf Nachdenken.
Das Dalton-Modell¶
Im Jahr 1803 griff der Chemiker und Lehrer John Dalton – inspiriert durch das vom Chemiker Joseph-Louis Proust formulierte Gesetz der konstanten Mengenverhältnisse – Demokrits Vorstellung von unteilbaren Materiebausteinen wieder auf. Er entwickelte ein Atommodell mit folgenden Hypothesen:
- Jede Materie besteht aus Grundbausteinen, den unteilbaren Atomen.
- Die Atome eines Elements sind untereinander gleich, die Atome verschiedener Elemente unterscheiden sich stets in ihrer Masse und Größe.
- Jeweils eine ganze Zahl an Atomen verschiedener Elemente bildet Verbindungen.
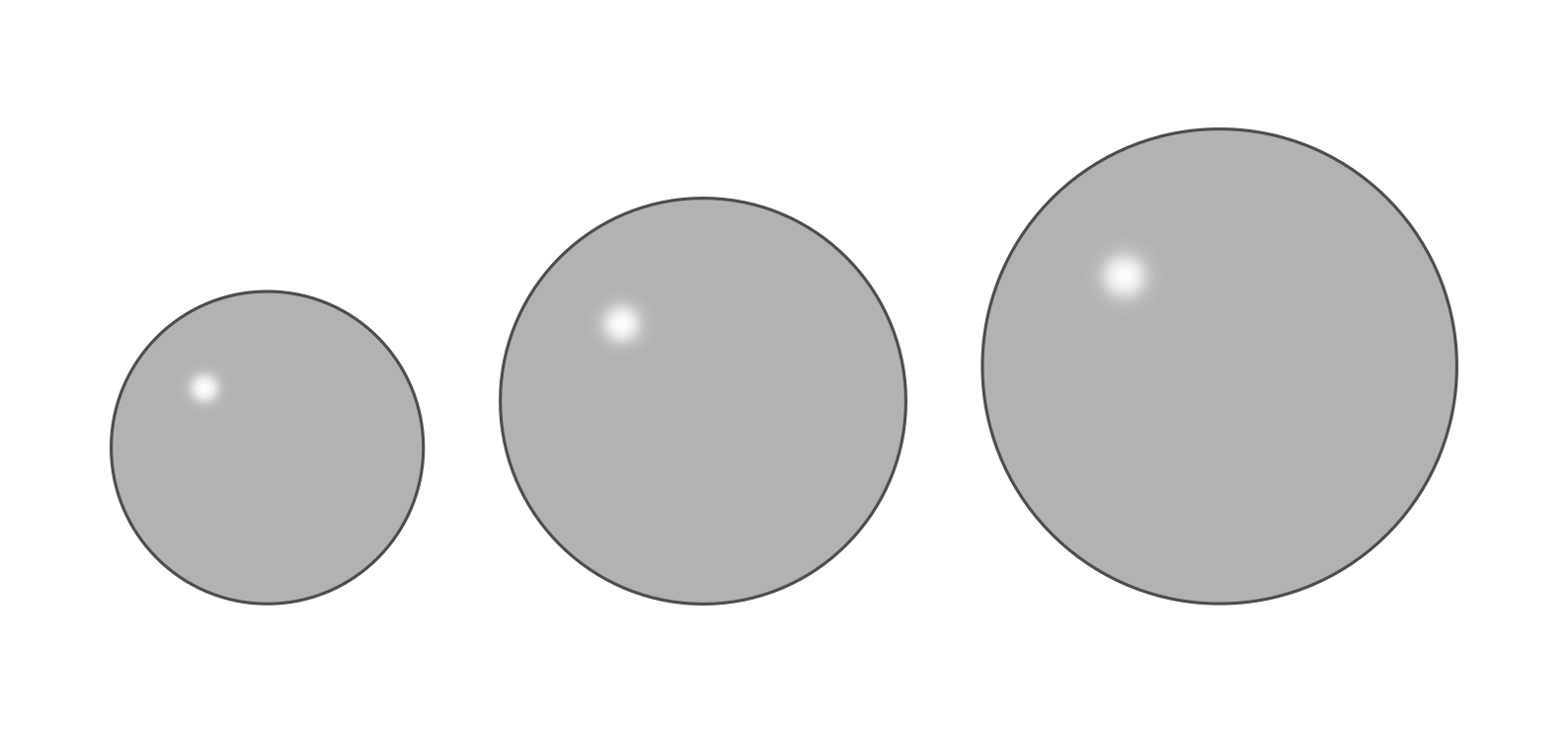
Das Atommodell nach Dalton: Unterschiedliche Elemente besitzen unterschiedlich große bzw. schwere Atome.
Durch diese Atomhypothese war Dalton in der Lage, das Gesetz von der Erhaltung der Masse, das Gesetz der konstanten Proportionen und das Gesetz der multiplen Proportionen zu erklären.
Das Thomson-Modell¶
Im Jahr 1897 entdeckte Joseph John Thomson bei Untersuchungen einer Glühkathode, dass es sich bei der austretenden Strahlung um einen Strom von Teilchen handeln müsse. Diese auf diese Weise entdeckten „Elektronen“ ließen sich durch ein Magnetfeld ablenken und besaßen eine fast 2000 mal kleinere Masse als das leichteste bekannte Atom (Wasserstoff).[1]
Da Thomson diesen „Elektronen“-Strahl aus jedem Metall durch Erhitzen gewinnen konnte, mussten diese Teilchen bereits im Metall enthalten sein; Atome konnten folglich nicht die kleinsten Bausteine der Materie bzw. unteilbar sein.
Thomson schlug daher im Jahr 1904 folgendes Atommodell vor:
- Jedes Atom besteht aus einer elektrisch positiv geladenen Kugel, in die elektrisch negativ geladene Elektronen eingelagert sind – wie Rosinen in einem Kuchen.
- Die Atome sind nach außen hin neutral. Sie können jedoch Elektronen abgeben oder zusätzliche aufnehmen.
- Bei der Abgabe von Elektronen entstehen aus den ursprünglich neutralen Atomen positiv geladene Ionen, bei der Aufnahme von Elektronen entstehen entsprechend negativ geladene Ionen.
Durch sein Atommodell konnte Thomson die Kathodenstrahlung sowie die Erkenntnisse aus der Elektrolyse-Forschung von Michael Faraday erklären.
Das Rutherford-Modell¶
Im Jahr 1911 führte Ernest Rutherford ein Experiment durch, bei dem
er einen Strahl radioaktiver Alpha-Teilchen 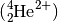 auf eine
dünne Goldfolie lenkte. Die meisten Alpha-Teilchen konnten die Goldfolie
ungehindert durchdringen, nur wenige wurden (teilweise sehr stark) abgelenkt.
auf eine
dünne Goldfolie lenkte. Die meisten Alpha-Teilchen konnten die Goldfolie
ungehindert durchdringen, nur wenige wurden (teilweise sehr stark) abgelenkt.
Dieses Ergebnis ließ sich nicht durch die Vorstellung kompakter Atomkugeln (Thomson-Modell) erklären. Der wesentliche Teil der Masse und die positive Ladung des Atoms mussten sich vielmehr in einem kleinen Bereich im Inneren befinden, an dem die auftreffenden Alpha-Teilchen abprallen konnten. Das meiste Volumen hingegen musste die masselose, negativ geladene und aufgrund der geringen Größe der Elektronen weitgehend „hohle“ Hülle des Atoms einnehmen.
Rutherford fasste seine Erkenntnisse in folgendem Atommodell zusammen:
- Das Atom besteht aus einem Atomkern und einer Atomhülle.
- Der Atomkern ist elektrisch positiv geladen und befindet sich im Zentrum des Atoms.
- Der Durchmesser des Atomkerns beträgt nur ein Zehntausendstel des gesamten Atomdurchmessers.
- In der Atomhülle befinden sich negativ geladene Elektronen, die um den Atomkern kreisen. (Durch ihre schnelle Bewegung verhindern die Elektronen, dass sie in den entgegengesetzt geladenen Atomkern stürzen.)
- Die Atomhülle ist ein fast „leerer“ Raum, da die Elektronen noch viel kleiner sind als der Atomkern.
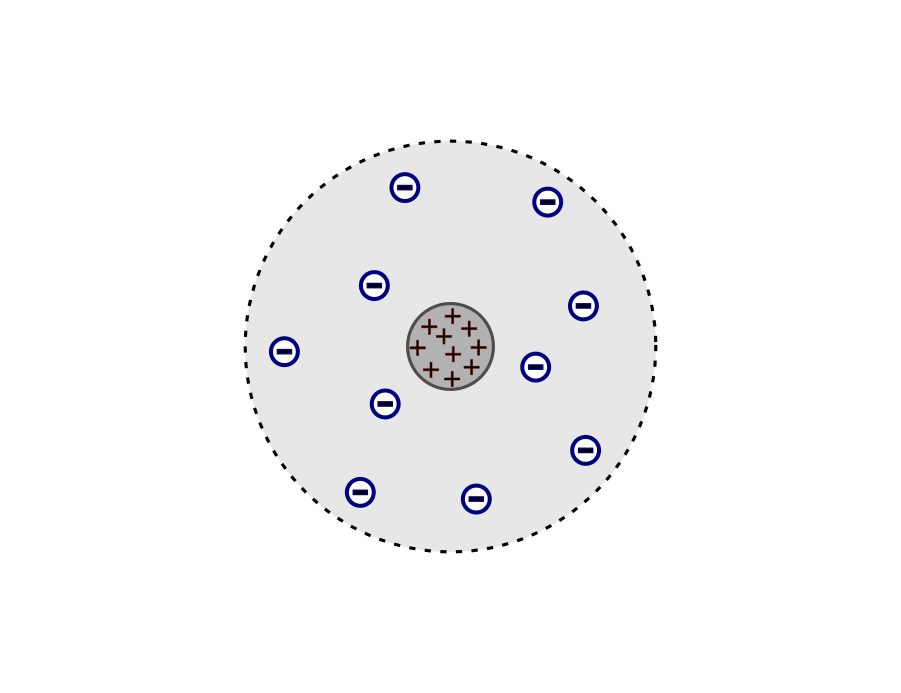
Das Atommodell nach Rutherford: Atom als positiv geladener Atomkern mit einer negativ geladenen Elektronenhülle.
Mit seinem Atommodell konnte Rutherford allerdings noch keine Aussagen über die Bahnform der Elektronen und über ihre Energieverteilung treffen.
Das Bohr-Modell¶
Im Jahr 1913 formulierte Niels Bohr ein Atommodell, das von einem planetenartigen Umlauf der Elektronen um den Atomkern ausgeht. Damit konnte er – beeinflusst durch die Quantentheorie Max Plancks und die Entdeckung des Photoeffekts durch Albert Einstein – erstmals die im Mikrokosmos stets in bestimmten Vielfachen auftretenden Energiesprünge deuten. Diese waren seit der Untersuchung der Spektren von Gasentladungsröhren – insbesondere seit der von Johann Jakob Balmer im Jahr 1885 gefundenen Formel[2] für die Verteilung der im Spektrum des Wasserstoffs auftretenden Wellenlängen – eines der größten Rätsel der damaligen Physik.
Bohr setzte in seinen Berechnungen die elektrostatische Anziehungskraft zwischen Elektron und Kern gleich der Zentrifugalkraft, die sich aus der Umlaufgeschwindigkeit des Elektrons ergibt. Hierdurch konnte er die Verteilung der Spektrallinien von Wasserstoff in allgemeiner Form[3] erklären.
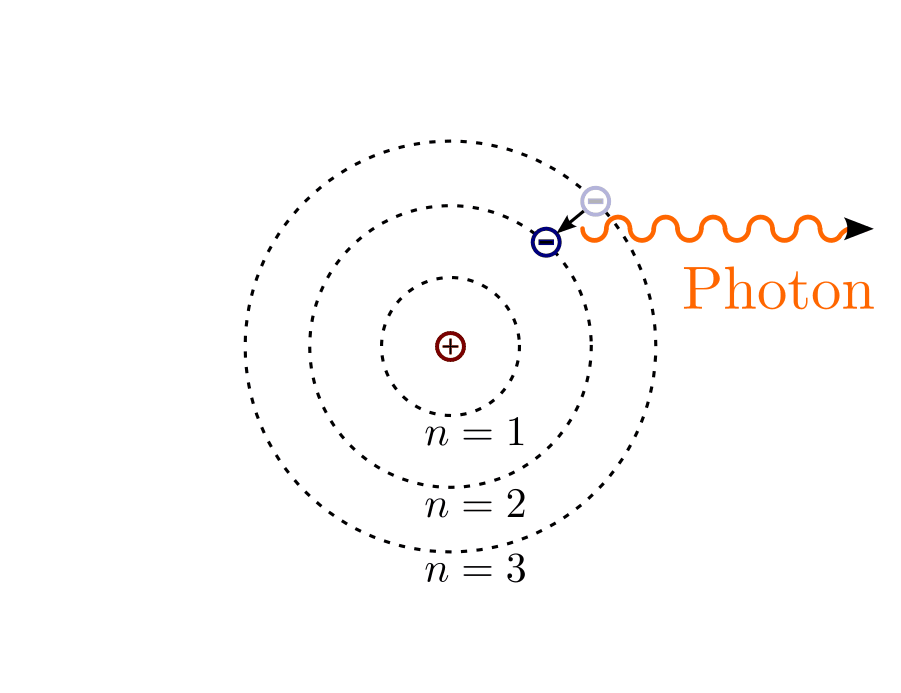
Das Atommodell für Wasserstoff nach Bohr: Jedes Elektron umkreist den Atomkern auf einer Kreisbahn. Beim Übergang eines Elektrons von einer äußeren Elektronenbahn in eine innere Elektronenbahn wird ein Lichtquant (Photon) ausgesendet.
Bohr war sich zudem bewusst, dass das Modell kreisförmiger Elektronenbahnen einen Widerspruch mit sich führte: Da jede Kreisbahn einer beschleunigten Bewegung entspricht und beschleunigte Ladungen elektromagnetische Wellen abstrahlen, müssten Elektronen ständig Energie abgeben und dadurch immer langsamer werden. Sie würden somit – angezogen von der positiven Ladung des Atomkerns – in nur wenigen Bruchteilen einer Sekunde spiralförmig in den Atomkern stürzen.
Um sein Atommodell zu retten, das auch mit anderen experimentellen Ergebnissen bestens übereinstimmte, führte Bohr die beiden folgenden Postulate ein[4]:
Die Elektronen umkreisen den Atomkern strahlungsfrei, d.h. ohne Abgabe von Energie, in bestimmten Bahnen. Dabei nimmt die Energie der Elektronen nur ganz bestimmte, durch die jeweilige Bahn charakterisierte Werte an.
Der Übergang zwischen einer kernfernen zu einer kernnahen Bahn erfolgt sprunghaft unter Abgabe einer Strahlung (eines Photons) mit der Frequenz
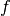 , so dass gilt:
, so dass gilt: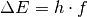
Hierbei ist 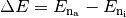 die
Energiedifferenz zwischen der äußeren und inneren Elektronenbahn und
die
Energiedifferenz zwischen der äußeren und inneren Elektronenbahn und ![h =
\unit[6,6256 \cdot 10^{-34}]{J \cdot s}](../_images/math/2f3cbfc36e9e6ca3ad16e112d2e273fb6e73f398.png) die Planck-Konstante. Im umgekehrten
Fall lässt sich ein Elektron durch ein Photon der entsprechenden Frequenz in
einen energiereicheren (weiter außen gelegenen) Zustand anheben.
die Planck-Konstante. Im umgekehrten
Fall lässt sich ein Elektron durch ein Photon der entsprechenden Frequenz in
einen energiereicheren (weiter außen gelegenen) Zustand anheben.
Die Sommerfeld-Erweiterung¶
Im Jahr 1916 formulierte Arnold Sommerfeld eine Erweiterung des
Bohrschein Atommodells. Es ging anstelle von Kreisbahnen allgemeiner von
elliptischen Bahnen der Elektronen um den Atomkern aus. Eine Ellipse besitzt
neben einer großen Halbachse, deren Größe nach Sommerfeld dem Radius einer
Kreisbahn im Bohrschen Atommodell und somit einem Energieniveau entsprach, auch
eine kleine Halbachse. Sommerfeld ging davon aus, dass auch die Größe dieser
Halbachse nur bestimmte Werte annehmen kann. Er führte somit neben der
„Hauptquantenzahl“  für das Energieniveau eine zusätzliche
„Nebenquantenzahl“
für das Energieniveau eine zusätzliche
„Nebenquantenzahl“  ein, welche im Wesentlichen die Form der Ellipse
bestimme.
ein, welche im Wesentlichen die Form der Ellipse
bestimme.
Arnold Sommerfeld konnte damit erklären, warum in den optischen Spektren eines Atoms – wie man dank einer höheren Auflösung zwischenzeitlich erkannte – nicht nur einzelne Linien, sondern eher mehrere sehr dicht beieinander liegende Linien auftreten. Diese „Feinstruktur“ war ein Hinweis darauf, dass in einem Atom mehrere Energieniveaus existieren, die sehr nahe zusammen liegen müssen. Nach Sommerfelds Vorstellung war durch das Vorhandensein von möglichen Ellipsenbahnen (abhängig vom Energieniveau) ein Grund für derartig feine Energie-Abstufungen gefunden.
Auch das Atommodell nach Sommerfeld kommt nicht ohne das Bohrschen Postulat aus, wonach Elektronen den Atomkern strahlungsfrei umkreisen. Die beiden Atommodelle von Bohr und Sommerfeld liefern für das Wasserstoff-Atom sehr genaue Ergebnisse, sind jedoch für Atome mit mehreren Elektronen unzureichend. Die Einführung einer Hauptquantenzahl durch Bohr und einer Nebenquantenzahl durch Sommerfeld hat sich dennoch, wie sich später herausstellte, als sinnvoll erwiesen.
Das Orbitalmodell¶
Das Orbitalmodell ist das bis heute genaueste Modell zur Beschreibung der Elektronenbahnen um den Atomkern. Grundlage hierfür waren fundamentale Erkenntnisse von Erwin Schrödinger und Werner Heisenberg in den Jahren 1926 und 1927, die unabhängig voneinander und mit verschiedenen mathematischen Zugängen die Quantenmechanik begründeten.
Die Elektronenbahnen im Orbitalmodell werden als Lösungen der so genannten
„Schrödinger-Gleichung“ angesehen. Diese entspricht formal einer Wellengleichung
und berücksichtigt den Welle-Teilchen-Dualismus der Elektronen.[5] Zudem kann
nach der „Unschärferelation“, die Werner Heisenberg formulierte, der Ort und
die Geschwindigkeit eines Teilchens niemals gleichzeitig mit beliebiger
Genauigkeit bestimmt werden. Es können damit nur bestimmte Raumbereiche
angegeben werden, innerhalb derer sich ein jeweiliges Elektron mit einer sehr
großen Wahrscheinlichkeit 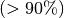 aufhält. Diese dreidimensionalen
Aufenthaltsräume werden Orbitale genannt.
aufhält. Diese dreidimensionalen
Aufenthaltsräume werden Orbitale genannt.
Die konkrete Form eines Orbitals hängt dabei von vier Quantenzahlen ab:
- Die Hauptquantenzahl
 gibt – wie in den Atommodellen nach Bohr und
Sommerfeld – das Energieniveau eines Elektrons an.
gibt – wie in den Atommodellen nach Bohr und
Sommerfeld – das Energieniveau eines Elektrons an. - Die Nebenquantenzahl
 legt die räumliche Form eines Orbitals und die
kleinen Energieunterschiede innerhalb eines Energieniveaus fest.
legt die räumliche Form eines Orbitals und die
kleinen Energieunterschiede innerhalb eines Energieniveaus fest. - Die Magnetquantenzahl
 berücksichtigt das unterschiedliche Verhalten
der Elektronen in einem von außen angelegten Magnetfeld.
berücksichtigt das unterschiedliche Verhalten
der Elektronen in einem von außen angelegten Magnetfeld. - Die Spinquantenzahl
 berücksichtigt die unterschiedlichen
Eigenrotationen der Elektronen, den so genannten Spin.
berücksichtigt die unterschiedlichen
Eigenrotationen der Elektronen, den so genannten Spin.
Jedes Elektron wird durch die obigen Quantenzahlen genau charakterisiert.
Auswahlregeln
Die vier Quantenzahlen 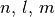 und
und  können nur
bestimmte, ganzzahlige Werte annehmen:
können nur
bestimmte, ganzzahlige Werte annehmen:
Für die Hauptquantenzahl
 gilt:
gilt:(1)¶
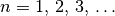
Die Werte der Hauptquantenzahlentsprechen somit formal den unterschiedlich weit vom Atomkern entfernten „Planetenbahnen“ des Bohrschen Atommodells.
Für die Nebenquantenzahl l gilt:
(2)¶

Die Werte der Nebenquantenzahl
 entsprechen formal den Abweichungen
von einer exakten Kreisbahn im Sommerfeldschen Atommodell. Bei einem
bestimmten Energieniveau
entsprechen formal den Abweichungen
von einer exakten Kreisbahn im Sommerfeldschen Atommodell. Bei einem
bestimmten Energieniveau  treten entsprechend auch
treten entsprechend auch  verschiedene Formen an Orbitalen auf.
verschiedene Formen an Orbitalen auf.
Für die Magnetquantenzahl
 gilt:
gilt:(3)¶

Bei einer bestimmten Nebenquantenzahl
 sind somit
sind somit 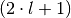 verschiedene Werte für die Magnetquantenzahl möglich. Diese Werte haben
eine unterschiedliche räumliche Ausrichtung der jeweiligen Orbitale zur
Folge.
verschiedene Werte für die Magnetquantenzahl möglich. Diese Werte haben
eine unterschiedliche räumliche Ausrichtung der jeweiligen Orbitale zur
Folge.
Für die Spinquantenzahl
 gilt:
gilt:(4)¶
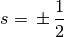
In jedem Orbital kann ein Elektron somit – unabhängig von den anderen Quantenzahlen – entweder den Spinzustand
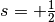 oder
oder
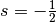 besitzen.
besitzen.
Nach dem im Jahr 1925 von Wolfgang Pauli formulierten und nach ihm benannten „Pauli-Prinzip“ müssen sich alle Elektronen eines Atoms in mindestens einer Quantenzahl unterscheiden.
Orbitalformen
Das Aussehen der Orbitale hängt von der Nebenquantenzahl  sowie von der
Magnetquantenzahl
sowie von der
Magnetquantenzahl  ab:
ab:
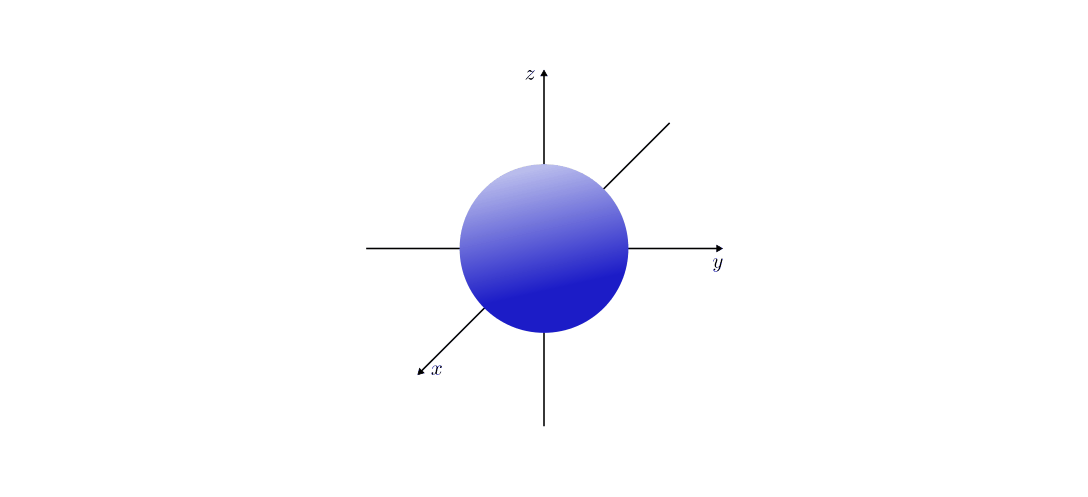
- Orbitale mit der Nebenquantenzahl
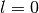 haben eine kugelförmige
Raumstruktur. Sie werden aus historischen Gründen auch als
„
haben eine kugelförmige
Raumstruktur. Sie werden aus historischen Gründen auch als
„ -Orbitale“ bezeichnet.
-Orbitale“ bezeichnet.
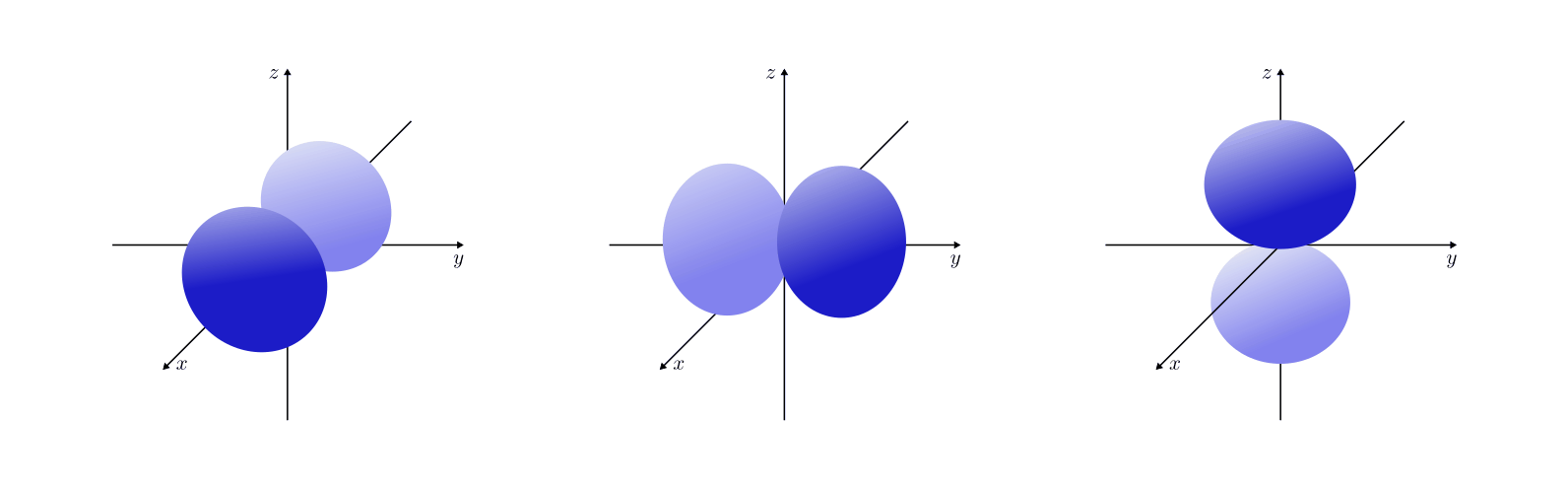
- Orbitale mit der Nebenquantenzahl
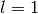 haben eine hantelförmige
Raumstruktur. Sie werden aus historischen Gründen auch als
„
haben eine hantelförmige
Raumstruktur. Sie werden aus historischen Gründen auch als
„ -Orbitale“ bezeichnet. In Abhängigkeit vom Wert der
Magnetquantenzahl
-Orbitale“ bezeichnet. In Abhängigkeit vom Wert der
Magnetquantenzahl 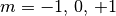 ergeben drei Orbitale, die sich
in ihrer räumlichen Ausrichtungen unterscheiden.
ergeben drei Orbitale, die sich
in ihrer räumlichen Ausrichtungen unterscheiden.
- Orbitale mit der Nebenquantenzahl
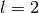 haben eine rosettenförmige
Raumstruktur. Sie werden aus historischen Gründen auch als
„
haben eine rosettenförmige
Raumstruktur. Sie werden aus historischen Gründen auch als
„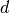 -Orbitale“ bezeichnet. In Abhängigkeit vom Wert der
Magnetquantenzahl
-Orbitale“ bezeichnet. In Abhängigkeit vom Wert der
Magnetquantenzahl  ergeben sich fünf
Orbitale, die sich in ihrer räumlichen Ausrichtung und Form unterscheiden.
ergeben sich fünf
Orbitale, die sich in ihrer räumlichen Ausrichtung und Form unterscheiden.
- Orbitale mit der Nebenquantenzahl
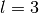 haben ebenfalls eine
rosettenförmige, noch weiter untergliederte Raumstruktur. Sie werden aus
historischen Gründen auch als „
haben ebenfalls eine
rosettenförmige, noch weiter untergliederte Raumstruktur. Sie werden aus
historischen Gründen auch als „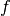 -Orbitale“ bezeichnet. In Abhängigkeit
vom Wert der Magnetquantenzahl
-Orbitale“ bezeichnet. In Abhängigkeit
vom Wert der Magnetquantenzahl 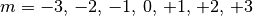 ergeben sich sieben Orbitale, die sich in ihrer räumlichen Ausrichtung
und Form unterscheiden.
ergeben sich sieben Orbitale, die sich in ihrer räumlichen Ausrichtung
und Form unterscheiden.
Theoretisch wären Atome mit weiteren Orbitalen denkbar. Praktisch hat man bislang jedoch nur Atome beobachten können, die sich mit Hilfe der obigen Orbitale beschreiben lassen.
Das Schalenmodell¶
Die konkrete Berechnung der Energieniveaus und der resultierenden Atomorbitale erfordert einen hohen mathematischen Aufwand. Viele Phänomene der Physik und Chemie lassen sich allerdings auch gut mit einem vereinfachten „Schalenmodell“ erklären, das einerseits an das Bohrsche Atommodell aufbaut, andererseits um Elemente aus dem Orbitalmodell erweitert ist.
Das Schalenmodell geht von folgender Vorstellung aus:
- Die Elektronen eines Atoms befinden sich auf konzentrischen Schalen um den Atomkern.
- Jede Schale stellt ein bestimmtes Energieniveau dar und kann eine bestimmte Zahl an Elektronen aufnehmen.
Die Hauptquantenzahl  gibt – von innen nach außen gezählt – die
Nummer der Schale an. Die maximale Anzahl an Elektronen auf Schale Nummer
gibt – von innen nach außen gezählt – die
Nummer der Schale an. Die maximale Anzahl an Elektronen auf Schale Nummer
 ist gleich
ist gleich 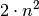 . Im Periodensystem der Elemente
entspricht die Schalennummer jeweils einer Periode (Reihe) an Elementen.
. Im Periodensystem der Elemente
entspricht die Schalennummer jeweils einer Periode (Reihe) an Elementen.
Die Orbitalformen, die sich aus der Nebenquantenzahl  ergeben, werden
Unterschalen genannt. Sie beinhalten, je nach Typ,
ergeben, werden
Unterschalen genannt. Sie beinhalten, je nach Typ, 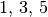 oder
oder
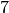 Orbitale, wodurch die Magnetquantenzahl
Orbitale, wodurch die Magnetquantenzahl  Berücksichtigung
findet. Jedes Orbital kann seinerseits zwei Elektronen mit unterschiedlichem
Spin
Berücksichtigung
findet. Jedes Orbital kann seinerseits zwei Elektronen mit unterschiedlichem
Spin 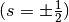 aufnehmen.
aufnehmen.
Nummer der Schale  |
Name der Unterschalen | Maximale Anzahl an Elektronen (gesamt) |
| 1 |  |
2 |
| 2 | 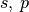 |
8 |
| 3 | 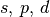 |
18 |
| 4 | 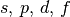 |
32 |
| 5 | 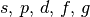 |
50 |
| 6 | 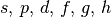 |
72 |
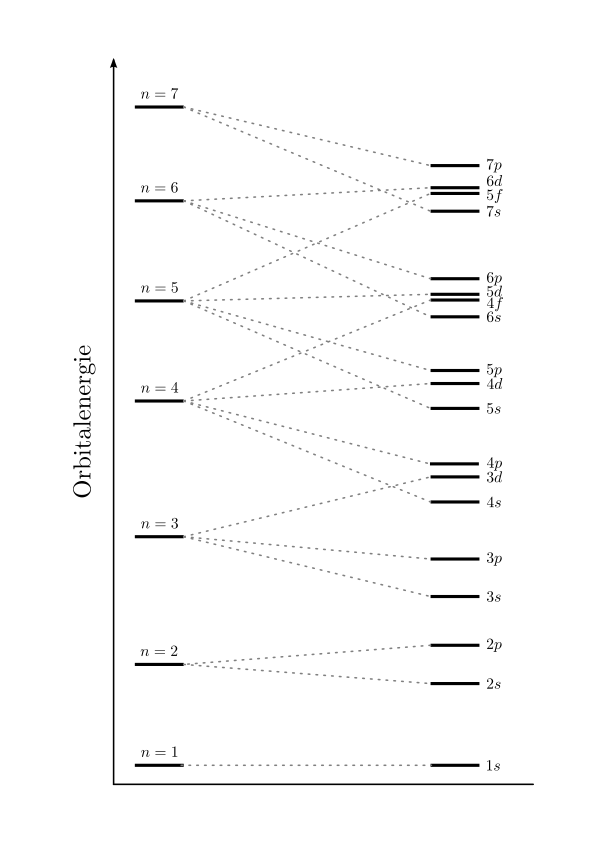
Hinzu kommende Elektronen füllen die einzelnen Orbitale eines Atoms nach
zunehmendem Energieniveau auf. Die Energieniveaus der Schalen, durch die
Hauptquantenzahl  bestimmt, spalten sich durch den Einfluss der übrigen
Quantenzahlen in entsprechend viele, jeweils nur einmalig vorkommende
Energieniveaus auf. Dies führt bei Atomen mit vier oder mehr Schalen dazu, dass
die Schalennummer
bestimmt, spalten sich durch den Einfluss der übrigen
Quantenzahlen in entsprechend viele, jeweils nur einmalig vorkommende
Energieniveaus auf. Dies führt bei Atomen mit vier oder mehr Schalen dazu, dass
die Schalennummer  die Auffüllreihenfolge nicht mehr alleinig bestimmt.
die Auffüllreihenfolge nicht mehr alleinig bestimmt.
Beispiel:
- Das
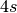 -Niveau besitzt eine niedrigere Energie als das
-Niveau besitzt eine niedrigere Energie als das
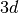 -Niveau. Entsprechend wird bei den ersten beiden Elementen der
vierten Periode (Kalium und Calcium) erst das
-Niveau. Entsprechend wird bei den ersten beiden Elementen der
vierten Periode (Kalium und Calcium) erst das 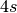 -Niveau mit zwei
Elektronen (Spin
-Niveau mit zwei
Elektronen (Spin 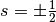 ) aufgefüllt, bevor bei den
Elementen Scandium bis Zink die
) aufgefüllt, bevor bei den
Elementen Scandium bis Zink die 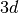 -Unterschale besetzt wird.
-Unterschale besetzt wird.
Die äußerste Schale, deren Besetzung für chemische und elektrische Vorgänge von besonderer Bedeutung ist, wird als „Valenzschale“ bezeichnet. Die sich auf ihr befindenden Elektronen werden „Valenzelektronen“ genannt. Im Periodensystem der Elemente entspricht die Anzahl an Valenzelektronen jeweils einer Gruppe (Spalte) an Elementen:
- Atome, deren energiereichstes Orbital ein
 - oder
- oder  -Orbital
ist, bilden die acht Hauptgruppen.
-Orbital
ist, bilden die acht Hauptgruppen. - Atome, deren energiereichstes Orbital ein
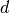 -Orbital ist, werden
Nebengruppenelemente genannt. Sie befinden sich im mittleren Teil des
Periodensystems.
-Orbital ist, werden
Nebengruppenelemente genannt. Sie befinden sich im mittleren Teil des
Periodensystems. - Atome, deren energiereichstes Orbital ein
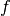 -Orbital ist, werden nach
den Elementen Lanthan bzw. Actinium als Lanthanoide bzw. Actinoide bezeichnet.
Sie werden im Periodensystem aus Gründen der Übersichtlichkeit meist als zwei
separate Zeilen im unteren Bereich „ausgelagert“.
-Orbital ist, werden nach
den Elementen Lanthan bzw. Actinium als Lanthanoide bzw. Actinoide bezeichnet.
Sie werden im Periodensystem aus Gründen der Übersichtlichkeit meist als zwei
separate Zeilen im unteren Bereich „ausgelagert“.
Chemische Bindungen lassen sich somit durch eine insgesamte Optimierung der Energiniveaus aller beteiligter Atome, physikalische Effekte wie Lichtemission und -Absorbtion durch Sprünge der Elektronen eines Atoms zwischen den verschiedenen Energieniveaus erklären.
Anmerkungen:
| [1] | Bereits Eugen Goldstein und William Crookes erkannten um das Jahr 1880 herum bei der Untersuchung von Gasentladungsröhren den „Teilchencharakter“ der Kathodenstrahlen. |
| [2] | Balmer entdeckte die Tatsache, dass sich die Wellenlängen
Hierbei stehen Weitere Spektrallinien des Wasserstoffs im nicht sichtbaren Bereich wurden später zu Ehren ihrer Entdecker Lyman-Serie (1906), Paschen-Serie (1908) und Brackett-Serie (1922) genannt. |
| [3] | Sämtliche Spektrallinien des Wasserstoffs lassen sich allgemein nach der folgenden „Balmer-Formel“ berechnen:
Hierbei steht |
| [4] | Ein Postulat ist ein Ansatz, der zu einem sinnvollen Ergebnis führt, auch wenn er theoretisch nicht begründet werden kann bzw. sogar widersprüchlich erscheint. |
| [5] | Der Welle-Teilchen-Dualismus wurde im Jahr 1924 von Louis de Broglie entdeckt. |



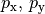 und
und 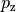 ).
).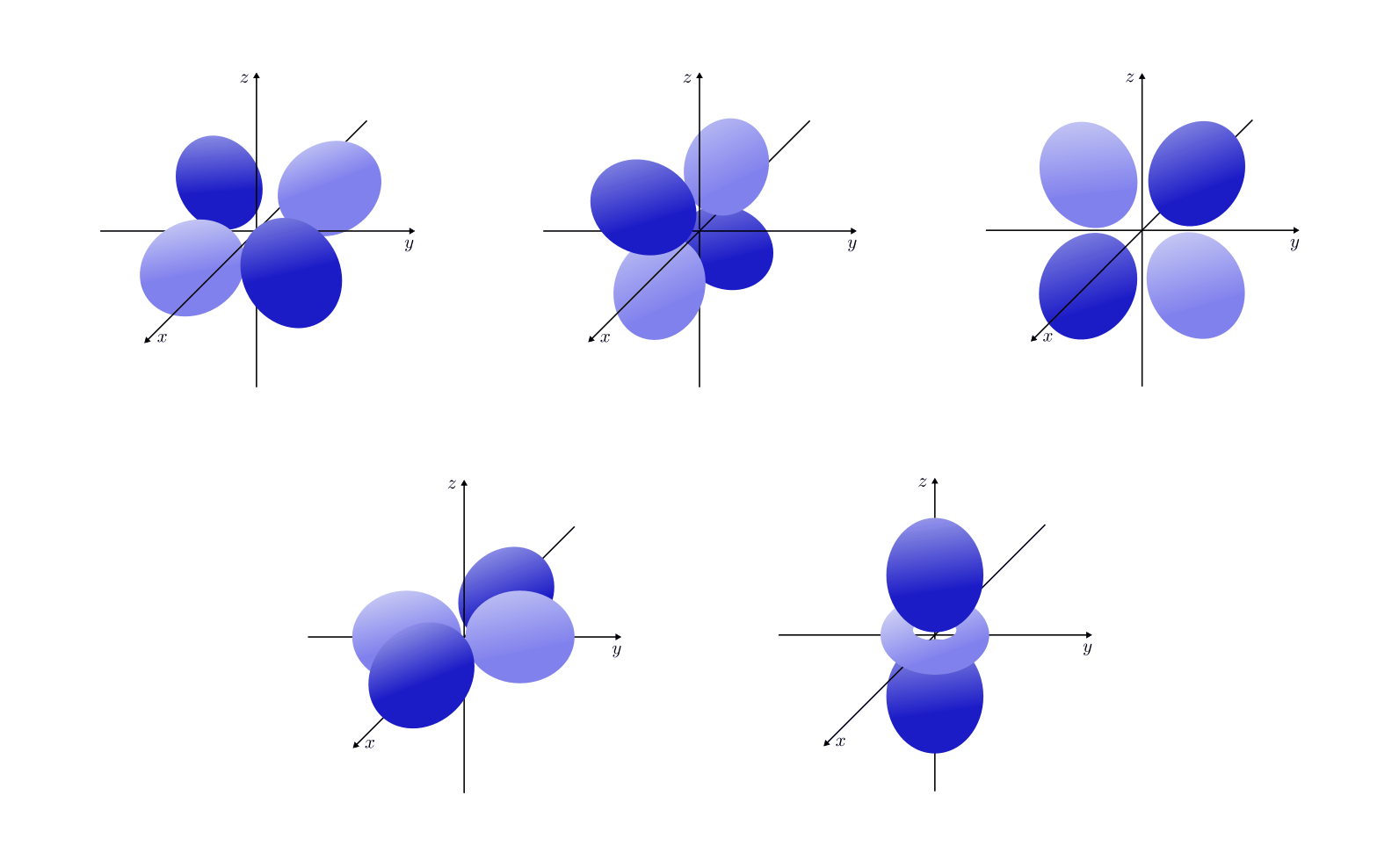
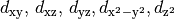 ).
).
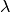 aller Linien im sichtbaren Teil des Wasserstoffspektrums durch eine
einfache mathematische Reihenformel beschreiben lassen:
aller Linien im sichtbaren Teil des Wasserstoffspektrums durch eine
einfache mathematische Reihenformel beschreiben lassen: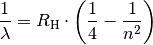
![R _{\rm{H}} = \unit[1,097 \cdot 10^7]{\frac{1}{m}
}](../_images/math/ecde8d51569593cd6e12b067b4ee89f2cae7da2f.png) für die Rydberg-Konstante und
für die Rydberg-Konstante und 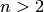 für eine ganze Zahl.
für eine ganze Zahl.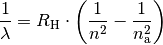
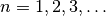 für die Elektronenbahn des
Ausgangszustandes und
für die Elektronenbahn des
Ausgangszustandes und  für die Elektronenbahn des
angeregten Zustands.
für die Elektronenbahn des
angeregten Zustands.