Koordinatensysteme¶
Koordinatensysteme haben die Aufgabe, die Lage eines Punktes in einer Ebene in übersichtlicher Weise und genau zu beschreiben. Es gibt verschiedene Möglichkeiten, wie diese Beschreibung erfolgen kann. Die zwei wichtigsten Koordinatensysteme, das kartesische und das polare, werden in den folgenden Abschnitten kurz beschrieben.
Das kartesische Koordinatensystem
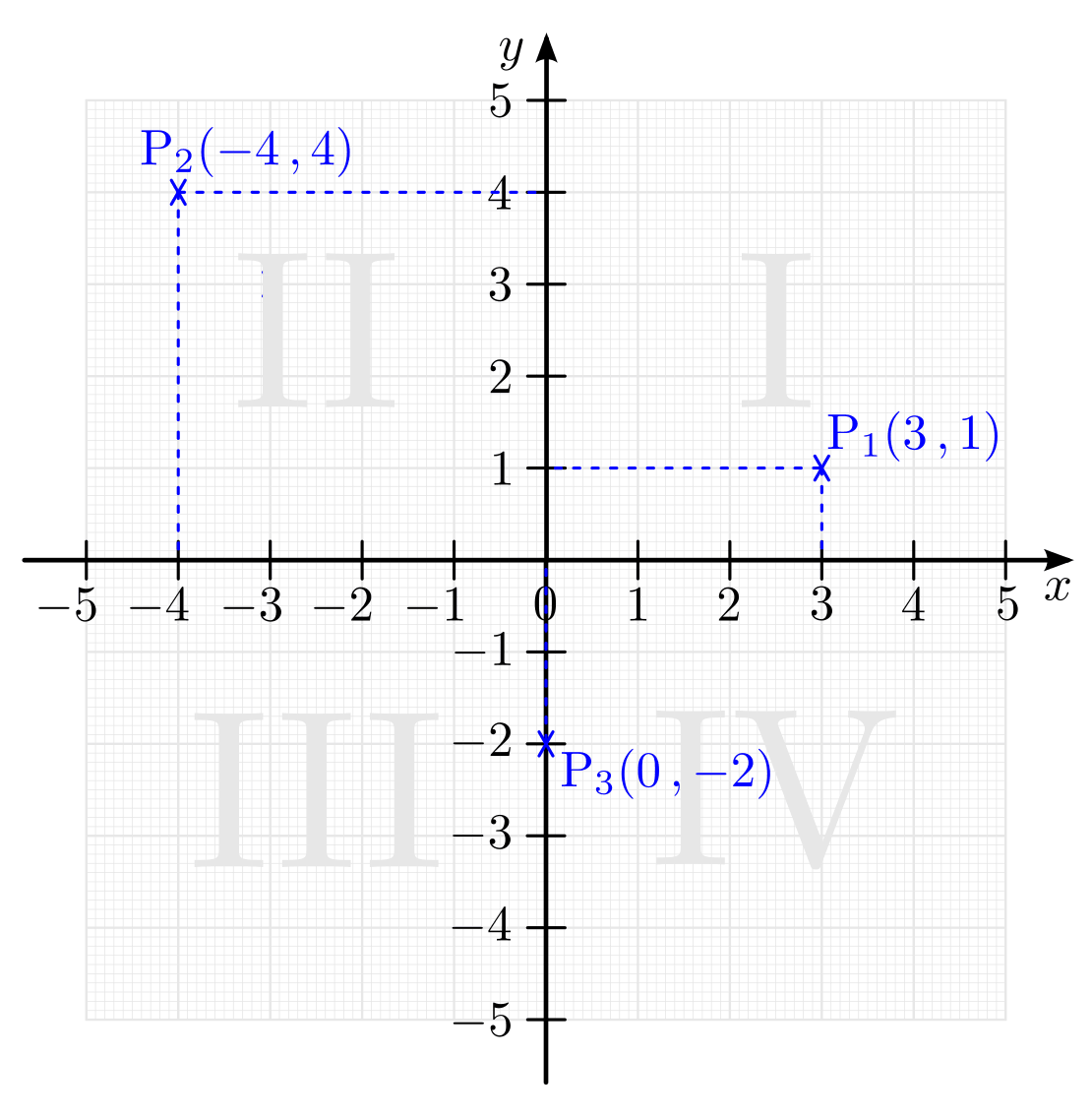
In einem so genannten kartesischen Koordinatensystem ist jeder Punkt der
Ebene durch seine Abstände zu den beiden Achsen festgelegt. Diese Abstände
werden durch zwei reelle Zahlen angegeben. Dadurch entspricht jedem Punkt
ein Zahlenpaar 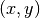 und umgekehrt jedem Zahlenpaar
und umgekehrt jedem Zahlenpaar 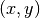 ein Punkt
ein Punkt  .
.
Die  -Achse wird bisweilen auch „Abszisse“, die
-Achse wird bisweilen auch „Abszisse“, die  -Achse
„Ordinate“ genannt. Auf der
-Achse
„Ordinate“ genannt. Auf der  -Achse wird nach rechts positiv, nach links
negativ gezählt, auf der
-Achse wird nach rechts positiv, nach links
negativ gezählt, auf der  -Achse nach oben positiv, nach unten negativ.
Die Ebene des Koordinatensystems wird durch die Achsen in vier Felder
aufgeteilt, die „Quadranten“ genannt und mit den römischen Ziffern
-Achse nach oben positiv, nach unten negativ.
Die Ebene des Koordinatensystems wird durch die Achsen in vier Felder
aufgeteilt, die „Quadranten“ genannt und mit den römischen Ziffern
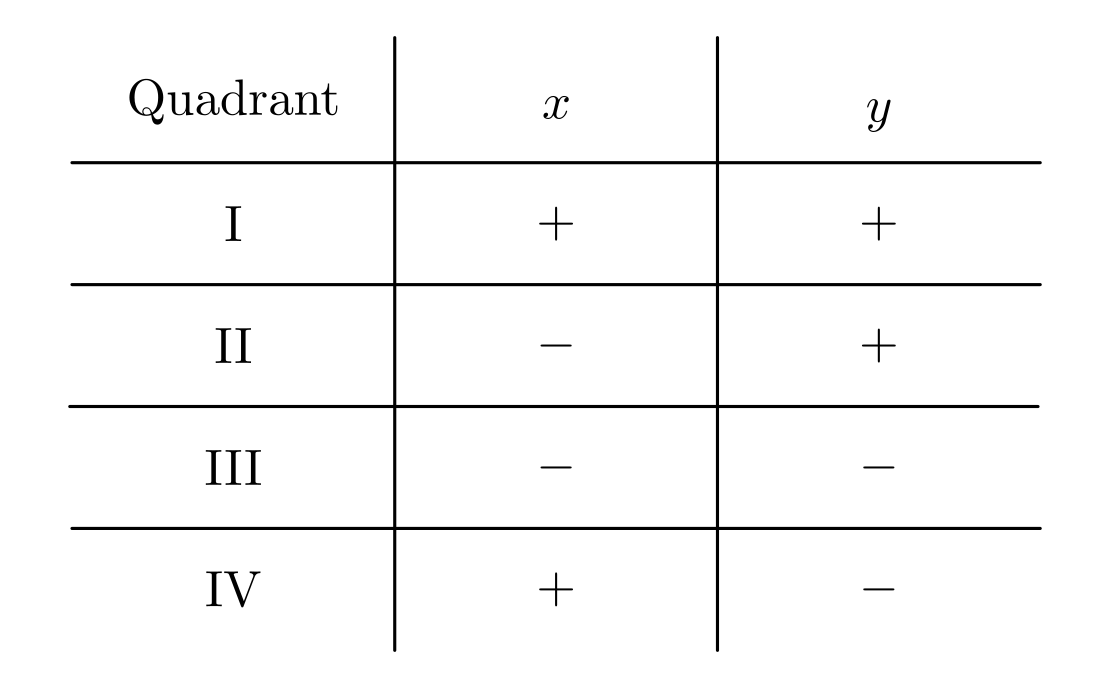
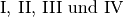 bezeichnet werden. In welchem Quadranten ein Punkt liegt, kann anhand der
Vorzeichen seiner Koordinaten abgelesen werden.
bezeichnet werden. In welchem Quadranten ein Punkt liegt, kann anhand der
Vorzeichen seiner Koordinaten abgelesen werden.
Kartesische Koordinatensysteme stellen die wohl wichtigste Grundlage für Punkt- und Linien-Diagramme in der Statistik dar; sie sind ebenso zur Darstellung der Ergebnismengen von Gleichungen und Ungleichungen in der Algebra sowie zur Darstellung von Funktionen in der Analysis unentbehrlich.
Das Polarkoordinatensystem
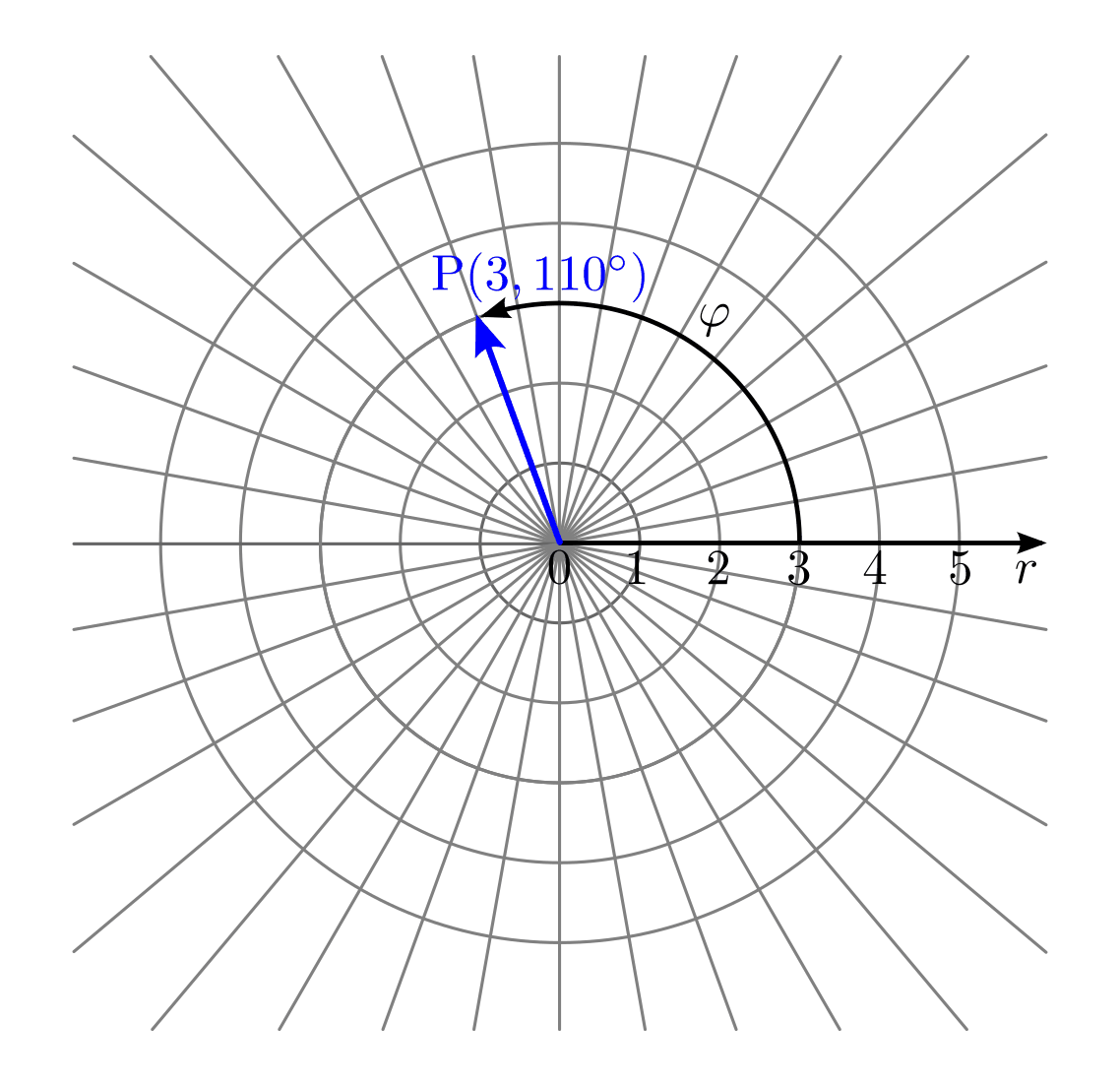
In einem so genannten Polarkoordinatensystem ist jeder Punkt  der
Ebene durch seinen Abstand
der
Ebene durch seinen Abstand  vom Koordinatenursprung und den Winkel
vom Koordinatenursprung und den Winkel
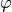 seiner Verbindungslinie mit dem Koordinatenursprung und der
Horizontalen eindeutig festgelegt.
seiner Verbindungslinie mit dem Koordinatenursprung und der
Horizontalen eindeutig festgelegt.
Die Koordinaten  und
und 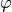 eines Punktes in einem
Polarkoordinatensystem und die Koordinaten
eines Punktes in einem
Polarkoordinatensystem und die Koordinaten  und
und  des selben
Punktes in einem kartesischen System lassen sich unmittelbar ineinander
umrechnen.
des selben
Punktes in einem kartesischen System lassen sich unmittelbar ineinander
umrechnen.
Sind  und
und  bekannt, so gilt für die Polarkoordinaten
bekannt, so gilt für die Polarkoordinaten  und
und 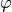 :
:
![r &= \sqrt{x^2 + y^2} \\[4pt]
\tan{\varphi} = \frac{y}{x} \quad &\text{bzw.} \quad \varphi =
\text{atan}\left(\frac{y}{x}\right)](../_images/math/9aa87e83049def6c2200d9aa924f5827722e74ff.png)
Sind im umgekehrten Fall  und
und 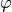 bekannt, so gilt für die
kartesischen Koordinaten
bekannt, so gilt für die
kartesischen Koordinaten  und
und  :
:
![x &= r \cdot \cos{\varphi} \\[4pt]
y &= r \cdot \sin{\varphi} \\](../_images/math/0720343ed1e57112213ec05bdfc4f8d1b2fa53f6.png)
Bei der Umrechnung zwischen kartesischen und polaren Koordinaten werden die drei trigonometrischen Größen Sinus, Cosinus und Tangens verwendet. Beide Koordinatensysteme haben Vor- und Nachteile, die je nach Art der mathematischen Aufgabenstellung überwiegen. In diesem Sinne ist kein Koordinatensystem dem anderen überlegen; das kartesische wird allerdings weitaus häufiger verwendet.