Laufzeiten von Algorithmen¶
Bisweilen können für die selbe Aufgabe mehrere Lösungen gefunden werden, die
sich teilweise jedoch erheblich in ihrer Effizienz unterscheiden. Bei der
Effizienz-Analyse eines Algorithmus, also eines „Rezepts“ zur Lösung eines
Problems, ist es insbesondere von Interesse, wie sich die Laufzeit in
Abhängigkeit von der Anzahl 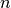 der zu bearbeitenden Daten ändert.
der zu bearbeitenden Daten ändert.
Zur Analyse von Laufzeiten sind prinzipiell zweierlei Vorgehensweisen möglich:
Mittels eines Benchmarks wird ein Programm oder Algorithmus mit einem möglichst typischen Satz an Daten aufgerufen und dabei die benötigte Zeit gemessen.
Ein Werkzeug, das hierfür unter Linux genutzt werden kann, ist gprof. Dieses Programm misst nicht nur die Laufzeit eines Programms und der im Programmverlauf aufgerufenen Funktionen, sondern zählt auch, wie häufig die einzelnen Funktionen aufgerufen wurden. Damit erhält man einen guten Überblick, welche Funktionen für eine weitergehende Analyse „wichtig“ sind.
Mit einer Laufzeit-Analyse kann anhand der Struktur des Quellcodes, beispielsweise anhand der Anzahl an Schleifendurchläufen, Lese- oder Schreibvorgängen, die Größenordnung der Laufzeit eines Algorithmus in Abhängigkeit von der Anzahl
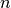 an zu bearbeiteten Daten abgeschätzt
werden.
an zu bearbeiteten Daten abgeschätzt
werden.
Die „Big-O“-Notation¶
Wie lange die Ausführung eines Algorithmus tatsächlich benötigt, hängt nicht
zuletzt von der Rechenleistung des Computers ab, auf dem der Code ausgeführt
wird; Benchmarks müssen daher auf einem einheitlichen System durchgeführt und
unter Angabe der Rechnerleistung (CPU, RAM, usw.) angegeben werden. Allgemeinere
Vergleiche sind hingegen möglich, welche die Laufzeit 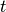 eines
Algorithmus allgemein als Funktion
eines
Algorithmus allgemein als Funktion 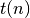 des Datenumfangs
des Datenumfangs 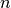 ausgedrückt wird. Wird beispielsweise im Verlauf eines Programms eine Funktion
mit einer konstanten Laufzeit
ausgedrückt wird. Wird beispielsweise im Verlauf eines Programms eine Funktion
mit einer konstanten Laufzeit  insgesamt
insgesamt 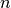 mal aufgerufen, so
ergibt sich dadurch eine Laufzeit von
mal aufgerufen, so
ergibt sich dadurch eine Laufzeit von 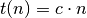 .
.
Beim Zählen von Laufzeiten wird üblicherweise die vereinfachende Vereinbarung, dass die folgenden Prozess-Schritte zur Ausführung jeweils eine Zeiteinheit benötigen:
- Jede Wertzuweisung
- Jeder Wertevergleich
- Jede Iteration einer Schleifenvariablen
Finden beispielsweise beim Durchlaufen einer Schleife 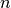 Iterationen
statt, so nimmt die Laufzeit für einen Aufruf einer solchen Schleife linear mit
Iterationen
statt, so nimmt die Laufzeit für einen Aufruf einer solchen Schleife linear mit
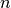 zu. Man sagt, dass in diesem Fall die Laufzeit proportional zur
Größenordnung von
zu. Man sagt, dass in diesem Fall die Laufzeit proportional zur
Größenordnung von 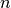 ist, und schreibt hierfür in Kurzform
ist, und schreibt hierfür in Kurzform
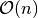 . Wird hingegen eine verschachtelte Liste mit
. Wird hingegen eine verschachtelte Liste mit 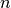 Teillisten durchlaufen, die wiederum
Teillisten durchlaufen, die wiederum 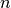 Einträge haben, so sind insgesamt
Einträge haben, so sind insgesamt
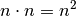 Iterationen nötig. Entsprechend ergibt sich für einen
Aufruf einer derartigen Schleife eine Laufzeit in der Größenordnung von
Iterationen nötig. Entsprechend ergibt sich für einen
Aufruf einer derartigen Schleife eine Laufzeit in der Größenordnung von
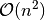 .
.
